Kuidas leida maatriksvektorit. Maatriksi karakteristiku võrrand

Ruutmaatriksi omavektor on selline, mis antud maatriksiga korrutades annab tulemuseks kollineaarse vektori. Lihtsate sõnadega, kui maatriksit korrutatakse omavektoriga, jääb viimane samaks, kuid korrutatakse mõne arvuga.

Definitsioon

Omavektor on nullist erinev vektor V, mis ruutmaatriksiga M korrutamisel muutub iseendaks, suurendatuna mingi arvu λ võrra. Algebralises tähistuses näeb see välja järgmine:

M × V = λ × V,

kus λ on maatriksi M omaväärtus.

Vaatleme numbrilist näidet. Kirjutamise hõlbustamiseks eraldatakse maatriksis olevad numbrid semikooloniga. Oletame, et meil on maatriks:

• M = 0; neli;
• 6; 10.

Korrutame selle veeruvektoriga:

• V = -2;

Maatriksi korrutamisel veeruvektoriga saame ka veeruvektori. Range matemaatiline keel valem 2 × 2 maatriksi korrutamiseks veeruvektoriga näeks välja järgmine:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 tähendab maatriksi M elementi, mis asub esimeses reas ja esimeses veerus, ning M22 on element, mis asub teises reas ja teises veerus. Meie maatriksi jaoks on need elemendid võrdsed M11 = 0, M12 = 4, M21 = 6, M22 10. Veeruvektori puhul on need väärtused võrdsed V11 = -2, V21 = 1. Selle valemi kohaselt saame järgmine tulemus ruutmaatriksi korrutised vektoriga:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Mugavuse huvides kirjutame veeruvektori ritta. Niisiis, me korrutasime ruutmaatriksi vektoriga (-2; 1), mille tulemuseks on vektor (4; -2). Ilmselgelt on see sama vektor, mis on korrutatud λ = -2-ga. Lambda tähistab sel juhul maatriksi omaväärtust.

Maatriksi omavektor on kollineaarne vektor, see tähendab objekt, mis maatriksiga korrutamisel ei muuda oma asukohta ruumis. Kollineaarsuse mõiste vektoralgebras on sarnane paralleelsuse mõistega geomeetrias. Geomeetrilises tõlgenduses on kollineaarsed vektorid paralleelselt suunatud segmendid erinevad pikkused. Alates Eukleidese ajast teame, et ühel sirgel on lõpmatu arv temaga paralleelseid sirgeid, seega on loogiline eeldada, et igal maatriksil on lõpmatu arv omavektoreid.

Eelmisest näitest on näha, et nii (-8; 4) kui ka (16; -8) ja (32, -16) võivad olla omavektorid. Kõik need on kollineaarsed vektorid, mis vastavad omaväärtusele λ = -2. Korrutades algse maatriksi nende vektoritega, saame tulemuseks ikkagi vektori, mis erineb algsest 2 korda. Seetõttu on omavektori leidmise ülesannete lahendamisel vaja leida ainult lineaarselt sõltumatud vektorobjektid. Kõige sagedamini on n × n maatriksi puhul n-s arv omavektoreid. Meie kalkulaator on mõeldud teist järku ruutmaatriksite analüüsimiseks, nii et peaaegu alati leitakse selle tulemusel kaks omavektorit, välja arvatud juhul, kui need langevad kokku.

Ülaltoodud näites teadsime eelnevalt algmaatriksi omavektorit ja määrasime visuaalselt lambda arvu. Praktikas juhtub aga kõik vastupidi: alguses on omaväärtused ja alles siis omavektorid.

Lahenduse algoritm

Vaatame uuesti algmaatriksit M ja proovime leida selle mõlemad omavektorid. Nii et maatriks näeb välja selline:

• M = 0; neli;
• 6; 10.

Alustuseks peame määrama omaväärtuse λ, mille jaoks peame arvutama järgmise maatriksi determinandi:

• (0 − λ); neli;
• 6; (10 − λ).

See maatriks saadakse tundmatu λ lahutamisel põhidiagonaali elementidest. Determinant määratakse standardvalemiga:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Kuna meie vektor ei tohi olla null, siis võtame saadud võrrandi lineaarselt sõltuvana ja võrdsustame oma determinandi detA nulliga.

(0 − λ) × (10 − λ) − 24 = 0

Avame sulud ja saame maatriksi iseloomuliku võrrandi:

λ 2 - 10 λ - 24 = 0

See on standardne ruutvõrrand, mis tuleb lahendada diskriminandi kaudu.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 = 100 + 96 \u003d 196

Diskriminandi juur on sqrt(D) = 14, seega λ1 = -2, λ2 = 12. Nüüd peame iga lambda väärtuse jaoks leidma omavektori. Avaldame süsteemi koefitsiendid λ = -2 korral.

• M − λ × E = 2; neli;
• 6; 12.

Selles valemis on E identiteedi maatriks. Saadud maatriksi põhjal koostame süsteemi lineaarvõrrandid:

2x + 4a = 6x + 12a

kus x ja y on omavektori elemendid.

Kogume kokku kõik X-id vasakul ja kõik Y-d paremal. Ilmselgelt - 4x = 8a. Jagage avaldis arvuga -4 ja saame x = -2y. Nüüd saame määrata maatriksi esimese omavektori, võttes mis tahes tundmatute väärtused (pidage meeles lineaarselt sõltuvate omavektorite lõpmatust). Võtame y = 1, siis x = -2. Seetõttu näeb esimene omavektor välja nagu V1 = (–2; 1). Tagasi artikli algusesse. Just selle vektorobjektiga korrutasime maatriksi omavektori kontseptsiooni demonstreerimiseks.

Nüüd leiame omavektori λ = 12 jaoks.

• M - λ × E = -12; neli
• 6; -2.

Koostame sama lineaarvõrrandisüsteemi;

• -12x + 4a = 6x -2a
• -18x = -6 a
• 3x=y.

Nüüd võtame x = 1, seega y = 3. Seega näeb teine ​​omavektor välja nagu V2 = (1; 3). Algmaatriksi korrutamisel selle vektoriga saadakse alati sama vektor korrutatuna 12-ga. See lõpetab lahendusalgoritmi. Nüüd teate, kuidas maatriksi omavektorit käsitsi määratleda.

• determinant;
• jälg, see tähendab põhidiagonaali elementide summa;
• järjestus, st maksimaalne lineaarselt sõltumatute ridade/veergude arv.

Programm töötab ülaltoodud algoritmi järgi, minimeerides lahendusprotsessi. Oluline on märkida, et programmis on lambda tähistatud tähega "c". Vaatame numbrilist näidet.

Programmi näide

Proovime defineerida omavektorid järgmise maatriksi jaoks:

• M = 5; 13;
• 4; 14.

Sisestame need väärtused kalkulaatori lahtritesse ja saame vastuse järgmisel kujul:

• Maatriksi aste: 2;
• Maatriksi determinant: 18;
• Maatriksi jälg: 19;
• Omavektori arvutamine: c 2 − 19,00c + 18,00 (karakteristiku võrrand);
• Omavektori arvutus: 18 (esimene lambda väärtus);
• Omavektori arvutus: 1 (teine ​​lambda väärtus);
• Vektori 1 võrrandisüsteem: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor 2 võrrandisüsteem: 4x1 + 13y1 = 4x1 + 13y1;
• Omavektor 1: (1; 1);
• Omavektor 2: (-3,25; 1).

Seega oleme saanud kaks lineaarselt sõltumatut omavektorit.

Järeldus

Lineaaralgebra ja analüütiline geomeetria on standardained igale inseneriteaduse esmakursuslasele. Suur hulk vektorite ja maatriksite kasutamine on hirmutav ning sellistes tülikates arvutustes on lihtne viga teha. Meie programm võimaldab õpilastel oma arvutusi kontrollida või omavektori leidmise probleemi automaatselt lahendada. Meie kataloogis on ka teisi lineaaralgebrakalkulaatoreid, kasutage neid õppetöös või töös.

Diagonaaltüüpi maatriksid on kõige lihtsamini paigutatud. Tekib küsimus, kas on võimalik leida alust, milles lineaaroperaatori maatriks oleks diagonaalse kujuga. Selline alus on olemas.
Olgu antud lineaarruum R n ja selles toimiv lineaaroperaator A; sel juhul võtab operaator A R n enda sisse ehk A:R n → R n .

Definitsioon. Nullist erinevat vektorit nimetatakse operaatori A omavektoriks, kui operaator A teiseneb temaga kollineaarseks vektoriks, st . Arvu λ nimetatakse omavektorile vastava operaatori A omaväärtuseks või omaväärtuseks .
Märgime mõningaid omaväärtuste ja omavektorite omadusi.
1. Omavektorite mis tahes lineaarne kombinatsioon operaatori A, mis vastab samale omaväärtusele λ, on sama omaväärtusega omavektor.
2. Omavektorid operaator A paarikaupa erinevate omaväärtustega λ 1 , λ 2 , …, λ m on lineaarselt sõltumatud.
3. Kui omaväärtused λ 1 =λ 2 = λ m = λ, siis omaväärtus λ vastab mitte rohkem kui m lineaarselt sõltumatule omavektorile.

Seega, kui on n lineaarselt sõltumatut omavektorit mis vastavad erinevatele omaväärtustele λ 1 , λ 2 , …, λ n , siis on nad lineaarselt sõltumatud, seega võib neid võtta ruumi R n aluseks. Leiame lineaaroperaatori A maatriksi kuju tema omavektorite alusel, mille puhul toimime operaatoriga A baasvektorite alusel: siis .
Seega on lineaarse operaatori A maatriksil oma omavektorite alusel diagonaalkuju ja operaatori A omaväärtused on diagonaalil.
Kas on veel mõni alus, mille puhul maatriksil on diagonaalne vorm? Sellele küsimusele annab vastuse järgmine teoreem.

Teoreem. Lineaaroperaatori A maatriksil aluses (i = 1..n) on diagonaalkuju siis ja ainult siis, kui kõik aluse vektorid on operaatori A omavektorid.

Omaväärtuste ja omavektorite leidmise reegel

Laske vektoril , kus x 1 , x 2 , …, x n - vektori koordinaadid baasi suhtes ja on omaväärtusele λ vastava lineaaroperaatori A omavektor, st. Selle seose saab kirjutada maatriksi kujul

. (*)

Võrrandit (*) võib pidada võrrandiks , ja leidmiseks, see tähendab, et meid huvitavad mittetriviaalsed lahendid, kuna omavektor ei saa olla null. On teada, et homogeense lineaarvõrrandisüsteemi mittetriviaalsed lahendid eksisteerivad siis ja ainult siis, kui det(A - λE) = 0. Seega, et λ oleks operaatori A omaväärtus, on vajalik ja piisav, et det(A - λE) ) = 0.
Kui võrrand (*) on üksikasjalikult kirjutatud koordinaatide kujul, saame lineaarse süsteemi homogeensed võrrandid:

(1)
kus on lineaaroperaatori maatriks.

Süsteemil (1) on nullist erinev lahendus, kui selle determinant D on võrdne nulliga

Saime omaväärtuste leidmiseks võrrandi.
Seda võrrandit nimetatakse karakteristikuks ja selle võrrandiks vasak pool- maatriksi (operaatori) A karakteristlik polünoom. Kui karakteristikul polünoomil pole reaaljuuri, siis maatriksil A ei ole omavektoreid ja seda ei saa taandada diagonaalkujule.
Olgu λ 1 , λ 2 , …, λ n karakteristiku võrrandi tegelikud juured ja nende hulgas võib olla kordi. Asendades need väärtused omakorda süsteemiga (1), leiame omavektorid.

Näide 12. Lineaaroperaator A toimib R 3-s vastavalt seadusele , kus x 1 , x 2 , .., x n on baasis oleva vektori koordinaadid , , . Leidke selle operaatori omaväärtused ja omavektorid.
Lahendus. Koostame selle operaatori maatriksi:
.
Koostame omavektorite koordinaatide määramise süsteemi:

Koostame iseloomuliku võrrandi ja lahendame selle:

.
λ 1,2 = -1, λ 3 = 3.
Asendades süsteemi λ = -1, saame:
või
Sest , siis on kaks sõltuvat muutujat ja üks vaba muutuja.
Olgu siis x 1 vaba tundmatu Me lahendame selle süsteemi mis tahes viisil ja leiame selle süsteemi üldlahenduse: Lahenduste põhisüsteem koosneb ühest lahendist, kuna n - r = 3 - 2 = 1.
Omaväärtusele λ = -1 vastav omavektorite hulk on kujul: , kus x 1 on mis tahes arv, mis ei ole null. Valime sellest hulgast ühe vektori, näiteks määrates x 1 = 1: .
Sarnaselt argumenteerides leiame omaväärtusele λ = 3 vastava omavektori: .
Ruumis R 3 koosneb baas kolmest lineaarselt sõltumatust vektorist, kuid oleme saanud ainult kaks lineaarselt sõltumatut omavektorit, millest R 3 baasi moodustada ei saa. Järelikult ei saa lineaaroperaatori maatriksit A ​​taandada diagonaalkujule.

Näide 13 Antud maatriks .
1. Tõesta, et vektor on maatriksi A omavektor. Leia sellele omavektorile vastav omaväärtus.
2. Leia alus, milles maatriksil A on diagonaalkuju.
Lahendus.
1. Kui , siis on omavektor

.
Vektor (1, 8, -1) on omavektor. Omaväärtus λ = -1.
Maatriksil on omavektoritest koosnevas baasis diagonaalvorm. Üks neist on kuulus. Leiame ülejäänud.
Otsime omavektoreid süsteemist:

Iseloomulik võrrand: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2–1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Leidke omaväärtusele λ = -3 vastav omavektor:

Selle süsteemi maatriksi auaste on võrdne kahega ja võrdub tundmatute arvuga, seetõttu on sellel süsteemil ainult nulllahendus x 1 = x 3 = 0. x 2 võib siin olla midagi muud kui null, näiteks x 2 = 1. Seega on vektor (0 ,1,0) omavektor, mis vastab väärtusele λ = -3. Kontrollime:
.
Kui λ = 1, siis saame süsteemi
Maatriksi auaste on kaks. Tõmmake viimane võrrand läbi.
Olgu x 3 vaba tundmatu. Siis x 1 \u003d -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = 9x 3.
Eeldades, et x 3 = 1, saame (-3,-9,1) - omaväärtusele λ = 1 vastav omavektor. Kontrollige:

.
Kuna omaväärtused on reaalsed ja erinevad, on neile vastavad vektorid lineaarselt sõltumatud, nii et neid saab R 3 aluseks võtta. Seega aluses , , maatriksil A on vorm:
.
Mitte iga lineaarse operaatori A:R n → R n maatriksit ei saa taandada diagonaalkujule, kuna mõne lineaaroperaatori puhul võib olla vähem kui n lineaarselt sõltumatut omavektorit. Kui aga maatriks on sümmeetriline, siis vastab täpselt m lineaarselt sõltumatut vektorit kordsusvõrrandi m juurele.

Definitsioon. Sümmeetriline maatriks on ruutmaatriks, milles põhidiagonaali suhtes sümmeetrilised elemendid on võrdsed, see tähendab, milles .
Märkused. 1. Kõik sümmeetrilise maatriksi omaväärtused on reaalsed.
2. Paarikaupa erinevatele omaväärtustele vastava sümmeetrilise maatriksi omavektorid on ortogonaalsed.
Üheks uuritud aparaadi arvukatest rakendustest käsitleme teist järku kõvera kuju määramise probleemi.

www.sait võimaldab teil leida. Sait teeb arvutused. Mõne sekundi pärast annab server välja õige otsus. Maatriksi iseloomulik võrrand on algebraline avaldis, mis leitakse determinandi arvutamise reegliga maatriksid maatriksid, samas kui põhidiagonaalil on diagonaalelementide ja muutuja väärtustes erinevusi. Arvutamisel võrgumaatriksi tunnusvõrrand, iga element maatriksid korrutatakse vastavate muude elementidega maatriksid. Otsige režiimis võrgus võimalik ainult ruudu jaoks maatriksid. Leia operatsioon võrgumaatriksi tunnusvõrrand taandub elementide korrutise algebralise summa arvutamiseks maatriksid determinandi leidmise tulemusena maatriksid, ainult kindlaksmääramise eesmärgil võrgumaatriksi tunnusvõrrand. See operatsioon on teoorias erilisel kohal maatriksid, võimaldab juurte abil leida omaväärtusi ja vektoreid. Ülesande leidmine võrgumaatriksi tunnusvõrrand on elementide korrutamine maatriksid koos nende saaduste hilisema summeerimisega teatud reegli järgi. www.sait leiab maatriksi tunnusvõrrand režiimis antud mõõde võrgus. arvutus võrgumaatriksi tunnusvõrrand antud dimensiooni jaoks on see numbriliste või sümboolsete koefitsientidega polünoomi leidmine, mis on leitud determinandi arvutamise reegliga maatriksid- vastavate elementide korrutiste summana maatriksid, ainult kindlaksmääramise eesmärgil võrgumaatriksi tunnusvõrrand. Ruudu muutuja suhtes polünoomi leidmine maatriksid, määratlusena maatriksi iseloomulik võrrand, teoreetiliselt levinud maatriksid. Polünoomi juurte väärtus võrgumaatriksi tunnusvõrrand kasutatakse omavektorite ja omaväärtuste määratlemiseks maatriksid. Kui aga determinant maatriksid siis on null maatriksi karakteristiku võrrand erinevalt vastupidisest on endiselt olemas maatriksid. Selleks, et arvutada maatriksi tunnusvõrrand või otsige mitut korraga maatriksite tunnusvõrrandid, peate kulutama palju aega ja vaeva, samas kui meie server leiab võrgumaatriksi tunnusvõrrand. Sel juhul vastus leidmisega võrgumaatriksi tunnusvõrrand on õige ja piisava täpsusega, isegi kui numbrid leidmisel võrgumaatriksi tunnusvõrrand saab olema irratsionaalne. Kohapeal www.sait märkide sisestamine on elementides lubatud maatriksid, see on võrgumaatriksi tunnusvõrrand saab arvutamisel esitada üldisel sümboolsel kujul karakteristiku võrrandi maatriks võrgus. Saadud vastust on kasulik kontrollida leidmisülesande lahendamisel võrgumaatriksi tunnusvõrrand saidi kasutades www.sait. Polünoomi arvutamise toimingu tegemisel - maatriksi karakteristlik võrrand, tuleb selle probleemi lahendamisel olla tähelepanelik ja äärmiselt kontsentreeritud. Meie sait omakorda aitab teil kontrollida oma otsust sellel teemal iseloomuliku võrrandi maatriks võrgus. Kui teil pole aega lahendatud probleemide pikaks kontrollimiseks, siis www.sait on kindlasti mugav tööriist otsimisel ja arvutamisel võrgumaatriksi tunnusvõrrand.

Definitsioon 9.3. Vektor X helistas oma vektor maatriksid AGA kui on selline number λ, et võrdsus kehtib: AGA X= λ X, ehk siis taotlemise tulemus X maatriksi poolt antud lineaarne teisendus AGA, on selle vektori korrutamine arvuga λ . Number ise λ helistas enda number maatriksid AGA.

Asendamine valemitega (9.3) x` j = λx j , saame võrrandisüsteemi omavektori koordinaatide määramiseks:

. (9.5)

See lineaarne homogeenne süsteem on mittetriviaalne lahendus ainult siis, kui selle peamine determinant on 0 (Crameri reegel). Kirjutades selle tingimuse kujul:

saame omaväärtuste määramiseks võrrandi λ helistas iseloomulik võrrand. Lühidalt võib seda esitada järgmiselt:

| A-λE | = 0, (9.6)

kuna selle vasak pool on maatriksi determinant A-λE. Polünoom suhtes λ | A-λE| helistas iseloomulik polünoom maatriksid a.

Iseloomuliku polünoomi omadused:

1) Lineaarse teisenduse iseloomulik polünoom ei sõltu aluse valikust. Tõestus. (vt (9.4)), kuid Järelikult,. Seega ei sõltu aluse valikust. Seega ja | A-λE| ei muutu uuele alusele üleminekul.

2) Kui maatriks AGA lineaarne teisendus on sümmeetriline(need. a ij = a ji), siis on kõik tunnusvõrrandi (9.6) juured reaalarvud.

Omaväärtuste ja omavektorite omadused:

1) Kui valime baasi omavektorite hulgast x 1, x 2, x 3 mis vastavad omaväärtustele λ 1 , λ 2 , λ 3 maatriksid AGA, siis sellel alusel on lineaarsel teisendusel A diagonaalmaatriks:

(9.7) Selle omaduse tõestus tuleneb omavektorite definitsioonist.

2) Kui teisenduse omaväärtused AGA on erinevad, siis on neile vastavad omavektorid lineaarselt sõltumatud.

3) Kui maatriksi iseloomulik polünoom AGA on kolm erinevat juurt, siis mingil alusel maatriks AGA on diagonaalse kujuga.

Leiame maatriksi omaväärtused ja omavektorid Teeme iseloomuliku võrrandi: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Leia igale leitud väärtusele vastavate omavektorite koordinaadid λ. (9.5) järeldub, et kui X (1) ={x 1, x 2, x 3) on omavektor, mis vastab λ 1 = -2, siis

on koostööl põhinev, kuid määramatu süsteem. Selle lahenduse võib kirjutada kui X (1) ={a,0,-a), kus a on suvaline arv. Eelkõige siis, kui vajate, et | x (1) |=1, X (1) =

Süsteemi asendamine (9.5) λ 2 =3, saame süsteemi teise omavektori koordinaatide määramiseks - x (2) ={y1,y2,y3}:

, kus X (2) ={b,-b,b) või tingimusel, et | x (2) |=1, x (2) =

Sest λ 3 = 6 leidke omavektor x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) või normaliseeritud versioonis

x (3) = Seda on näha X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = eKr- 2bc + bc= 0. Seega on selle maatriksi omavektorid paarikaupa ortogonaalsed.

10. loeng

Ruutvormid ja nende seos sümmeetriliste maatriksitega. Sümmeetrilise maatriksi omavektorite ja omaväärtuste omadused. Ruutvormi taandamine kanooniliseks vormiks.

Definitsioon 10.1.ruutvorm reaalsed muutujad x 1, x 2,…, x n nimetatakse nende muutujate suhtes teise astme polünoomi, mis ei sisalda vaba liiget ja esimese astme liikmeid.

Ruutvormide näited:

(n = 2),

(n = 3). (10.1)

Tuletage meelde viimases loengus antud sümmeetrilise maatriksi definitsiooni:

Definitsioon 10.2. Ruutmaatriksit nimetatakse sümmeetriline, kui , see tähendab, kui põhidiagonaali suhtes sümmeetrilised maatriksi elemendid on võrdsed.

Sümmeetrilise maatriksi omaväärtuste ja omavektorite omadused:

1) Kõik sümmeetrilise maatriksi omaväärtused on reaalsed.

Tõend (eest n = 2).

Laske maatriksil AGA tundub, et: . Teeme iseloomuliku võrrandi:

(10.2) Leidke diskriminant:

Seetõttu on võrrandil ainult reaalsed juured.

2) Sümmeetrilise maatriksi omavektorid on ortogonaalsed.

Tõend (eest n= 2).

Omavektorite ja koordinaadid peavad täitma võrrandeid.

HOMOGEENSTE LINEAARVÕRRANDITE SÜSTEEM

Homogeensete lineaarvõrrandite süsteem on vormi süsteem

Selge on see, et antud juhul , sest nende determinantide ühe veeru kõik elemendid on võrdsed nulliga.

Kuna tundmatud leitakse valemite abil , siis juhul, kui Δ ≠ 0, on süsteemil unikaalne nulllahendus x = y = z= 0. Paljude ülesannete puhul pakub aga huvi küsimus, kas homogeensel süsteemil on muid lahendusi kui null.

Teoreem. Et lineaarsete homogeensete võrrandite süsteemil oleks nullist erinev lahendus, on vajalik ja piisav, et Δ ≠ 0.

Seega, kui determinant on Δ ≠ 0, on süsteemil ainulaadne lahendus. Kui Δ ≠ 0, siis on lineaarsete homogeensete võrrandite süsteemil lõpmatu arv lahendeid.

Näited.

Omavektorid ja maatriksi omaväärtused

Olgu antud ruutmaatriks , X on mingi maatriks-veerg, mille kõrgus langeb kokku maatriksi järjekorraga A. .

Paljude probleemide puhul tuleb arvestada võrrandiga X

kus λ on mingi arv. On selge, et mis tahes λ korral on sellel võrrandil nulllahendus.

Nimetatakse arvu λ, mille jaoks sellel võrrandil on nullist erinevad lahendid omaväärtus maatriksid A, a X sellise λ jaoks nimetatakse oma vektor maatriksid A.

Leiame maatriksi omavektori A. Kuna E∙X = X, siis saab maatriksvõrrandi ümber kirjutada kujul või . Laiendatud kujul saab selle võrrandi ümber kirjutada lineaarsete võrrandite süsteemiks. Tõesti .

Ning seetõttu

Niisiis saime koordinaatide määramiseks homogeensete lineaarvõrrandite süsteemi x 1, x2, x 3 vektor X. Et süsteemis oleks nullist erineva lahendusi, on vajalik ja piisav, et süsteemi determinant oleks võrdne nulliga, s.t.

See on 3. astme võrrand λ suhtes. Seda nimetatakse iseloomulik võrrand maatriksid A ja seda kasutatakse omaväärtuste λ määramiseks.

Iga omaväärtus λ vastab omavektorile X, mille koordinaadid määratakse süsteemist vastava väärtusega λ.

Näited.

VEKTORALGEBRA. VEKTORMÕISTE

Erinevate füüsikaharude uurimisel on suurused, mis määratakse täielikult kindlaks nende arvväärtuste seadmisega, näiteks pikkus, pindala, mass, temperatuur jne. Selliseid väärtusi nimetatakse skalaarideks. Kuid lisaks neile on ka suurused, mille määramiseks on lisaks arvväärtusele vaja teada ka nende suunda ruumis, näiteks kehale mõjuvat jõudu, kiirust ja kiirendust. kehast, kui see ruumis liigub, pinge magnetväli antud ruumipunktis jne. Selliseid suurusi nimetatakse vektorsuurusteks.

Tutvustame ranget määratlust.

Suunatud segment Nimetame lõigu, mille otste suhtes on teada, milline neist on esimene ja milline teine.

Vektor nimetatakse suunatud segmenti, millel on teatud pikkus, st. See on teatud pikkusega segment, milles üks seda piiravatest punktidest võetakse alguseks ja teine ​​​​lõpuks. Kui a A on vektori algus, B on selle lõpp, siis tähistatakse vektorit sümboliga, lisaks tähistatakse vektorit sageli ühe tähega . Joonisel on vektorit tähistatud segmendiga ja selle suunda noolega.

moodul või pikk vektorit nimetatakse seda määratleva suunatud segmendi pikkuseks. Tähistatakse || või ||.

Nn nullvektorit, mille algus ja lõpp langevad kokku, nimetatakse ka vektoriteks. See on märgistatud. Nullvektoril puudub kindel suund ja selle moodul on võrdne nulliga ||=0.

Vektoreid ja nimetatakse kollineaarne kui need asuvad samal joonel või paralleelsetel joontel. Sel juhul, kui vektorid ja on võrdselt suunatud, kirjutame , vastupidiselt.

Nimetatakse vektoreid, mis asuvad sama tasapinnaga paralleelsetel sirgel koplanaarne.

Kaks vektorit ja nimetatakse võrdne kui need on kollineaarsed, on sama suunaga ja võrdse pikkusega. Sel juhul kirjutage.

Vektorite võrdsuse definitsioonist tuleneb, et vektorit saab endaga paralleelselt nihutada, asetades selle alguspunkti ükskõik millisesse ruumipunkti.

Näiteks.

LINEAARSED TEHTUD VEKTORIDELE

1. Vektori korrutamine arvuga.

   Vektori korrutis arvuga λ on uus vektor, nii et:

   Vektori ja arvu λ korrutist tähistatakse .

   

   Näiteks, on vektor, mis osutab vektoriga samas suunas ja mille pikkus on poole vektori pikkusest.

   Sisestatud toimingul on järgmine omadused:

2. Vektorite liitmine.

   Olgu ja kaks suvalist vektorit. Võtke suvaline punkt O ja konstrueerida vektor . Pärast seda punktist A kõrvale panema vektor . Nimetatakse vektor, mis ühendab esimese vektori alguse teise lõpuga summa nendest vektoritest ja on tähistatud .

   

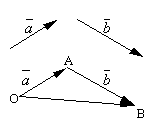
   Vektorliitmise formuleeritud definitsiooni nimetatakse rööpküliku reegel, kuna sama vektorite summa võib saada järgmiselt. Pange punktist kõrvale O vektorid ja . Koostage nendele vektoritele rööpkülik OABC. Kuna vektorid , siis vektor , mis on tipust tõmmatud rööpküliku diagonaal O, on ilmselt vektorite summa.

   

   Järgmist on lihtne kontrollida vektori liitmise omadused.

3. Vektorite erinevus.

   Nimetatakse antud vektoriga kollineaarset vektorit, mis on võrdne pikkusega ja vastassuunas vastupidine vektor vektori jaoks ja seda tähistatakse . Vastandvektorit võib pidada vektori arvuga λ = –1 korrutamise tulemuseks: .