מצא את נפח הפירמידה המשולשת בבסיס. נפח פירמידה

פירמידה היא פוליידרון עם מצולע בבסיסו. כל הפרצופים, בתורם, יוצרים משולשים המתכנסים בקודקוד אחד. פירמידות הן משולשות, מרובעיות וכן הלאה. כדי לקבוע איזו פירמידה לפניכם, מספיק לספור את מספר הפינות בבסיסה. ההגדרה של "גובה פירמידה" נמצאת לעתים קרובות מאוד בבעיות גיאומטריה ב מערכת של ביהס. במאמר ננסה לשקול דרכים שונותהמיקום שלה.

חלקים מהפירמידה

כל פירמידה מורכבת מהאלמנטים הבאים:

• פנים צדדיות בעלות שלוש פינות ומתכנסות בחלק העליון;
• אפוטם מייצג את הגובה היורד מראשו;
• החלק העליון של הפירמידה הוא נקודה המחברת את הקצוות הצדדיים, אך אינה שוכבת במישור הבסיס;
• בסיס הוא מצולע שאינו מכיל קודקוד;
• גובה הפירמידה הוא קטע שחותך את החלק העליון של הפירמידה ויוצר זווית ישרה עם הבסיס שלה.

כיצד למצוא את גובה הפירמידה אם נפחה ידוע

באמצעות הנוסחה V \u003d (S * h) / 3 (בנוסחה V הוא הנפח, S הוא שטח הבסיס, h הוא גובה הפירמידה), אנו מוצאים כי h \u003d (3 * V) / S . כדי לאחד את החומר, בואו נפתור מיד את הבעיה. הבסיס המשולש הוא 50 ס"מ 2 בעוד נפחו הוא 125 ס"מ 3. גובה הפירמידה המשולשת אינו ידוע, אותו אנו צריכים למצוא. הכל פשוט כאן: אנחנו מכניסים את הנתונים לנוסחה שלנו. אנחנו מקבלים h \u003d (3 * 125) / 50 \u003d 7.5 ס"מ.

איך למצוא את גובה הפירמידה אם אורך האלכסון והקצה שלו ידועים

כזכור, גובה הפירמידה יוצר זווית ישרה עם הבסיס שלה. וזה אומר שהגובה, הקצה וחצי האלכסון יוצרים ביחד רבים, כמובן, זוכרים את משפט פיתגורס. לדעת שני מימדים, לא יהיה קשה למצוא את הערך השלישי. זכור את המשפט הידוע a² = b² + c², כאשר a הוא התחתון, ובמקרה שלנו קצה הפירמידה; b - הרגל הראשונה או חצי האלכסון ו-c - בהתאמה, הרגל השנייה, או גובה הפירמידה. מנוסחה זו, c² = a² - b².

עכשיו הבעיה: בפירמידה רגילה האלכסון הוא 20 ס"מ, בעוד שאורך הקצה הוא 30 ס"מ. צריך למצוא את הגובה. אנו פותרים: c² \u003d 30² - 20² \u003d 900-400 \u003d 500. לפיכך c \u003d √ 500 \u003d בערך 22.4.

כיצד למצוא את הגובה של פירמידה קטומה

זהו מצולע בעל חתך מקביל לבסיסו. גובהה של פירמידה קטומה הוא הקטע המחבר את שני הבסיסים שלה. גובה ניתן למצוא ב פירמידה נכונה, אם ידועים אורכי האלכסונים של שני הבסיסים, כמו גם קצה הפירמידה. תנו לאלכסון של הבסיס הגדול יותר להיות d1, בעוד שהאלכסון של הבסיס הקטן יותר הוא d2, ולקצה יש אורך l. כדי למצוא את הגובה, ניתן להוריד את הגבהים משתי הנקודות ההפוכות העליונות של התרשים לבסיסו. אנו רואים שיש לנו שני משולשים ישרי זווית, נותר למצוא את אורכי רגליהם. לשם כך, נחסר את האלכסון הקטן מהאלכסון הגדול יותר ונחלק ב-2. אז נמצא רגל אחת: a \u003d (d1-d2) / 2. לאחר מכן, לפי משפט פיתגורס, נותר לנו רק למצוא את הרגל השנייה, שהיא גובה הפירמידה.

עכשיו בואו נסתכל על כל העניין הזה בפועל. יש לנו משימה לפנינו. לפירמידה הקטומה יש ריבוע בבסיס, אורך האלכסון של הבסיס הגדול הוא 10 ס"מ, בעוד הקטן הוא 6 ס"מ, והקצה הוא 4 ס"מ. נדרש למצוא את הגובה. מלכתחילה, אנו מוצאים רגל אחת: \u003d (10-6) / 2 \u003d 2 ס"מ. רגל אחת היא 2 ס"מ, והתחתון הוא 4 ס"מ. מסתבר שהרגל השנייה או הגובה יהיו 16- 4 \u003d 12, כלומר, h \u003d √12 = כ 3.5 ס"מ.

המילה "פירמידה" קשורה באופן לא רצוני לענקים המלכותיים במצרים, השומרים נאמנה על שלום הפרעונים. אולי בגלל זה הפירמידה מוכרת ללא ספק על ידי כולם, אפילו ילדים.

עם זאת, בואו ננסה לתת לזה הגדרה גיאומטרית. הבה נדמיין כמה נקודות (A1, A2,..., An) במישור ועוד אחת (E) שאינה שייכת לו. לכן, אם נקודה E (למעלה) מחוברת לקודקודים של המצולע שנוצרו על ידי נקודות A1, A2, ..., An (בסיס), אתה מקבל פולידרון, שנקרא פירמידה. ברור שלמצולע בבסיס הפירמידה יכול להיות כל מספר של קודקודים, ובהתאם למספרם, הפירמידה יכולה להיקרא משולשת ומרובעת, מחומשת וכו'.

אם תסתכלו מקרוב על הפירמידה, יתברר מדוע גם היא מוגדרת אחרת – כ דמות גיאומטרית, שיש לו מצולע בבסיס, ומשולשים המאוחדים על ידי קודקוד משותף כשפני צד.

מכיוון שהפירמידה היא דמות מרחבית, אז יש לה גם מאפיין כמותי כזה, שכן הוא מחושב מהשליש השווה הידוע של מכפלת בסיס הפירמידה וגובהה:

נפח הפירמידה, בעת גזירת הנוסחה, מחושב תחילה עבור פירמידה משולשת, בהתבסס על יחס קבוע המקשר את הערך הזה לנפח מנסרה משולשת, שיש לו אותו בסיס וגובה, שמסתבר שהוא פי שלושה מהנפח.

ומכיוון שכל פירמידה מחולקת למשולשים, ונפחה אינו תלוי בקונסטרוקציות שבוצעו בהוכחה, תקפות נוסחת הנפח הנ"ל ברורה.

עומדות בנפרד בין כל הפירמידות הנכונות, שבהן נמצא הבסיס. באשר, הוא צריך "להסתיים" במרכז הבסיס.

במקרה של מצולע לא סדיר בבסיס, כדי לחשב את שטח הבסיס, תצטרך:

• לשבור אותו למשולשים ומרובעים;

• לחשב את השטח של כל אחד מהם;

• להוסיף את הנתונים שהתקבלו.

במקרה של מצולע רגיל בבסיס הפירמידה, השטח שלו מחושב באמצעות נוסחאות מוכנות, ולכן נפח פירמידה רגיל מחושב בפשטות רבה.

לדוגמה, כדי לחשב את הנפח של פירמידה מרובעת, אם היא רגילה, אורך הצלע של מרובע רגיל (ריבוע) בבסיס מרובע, וכפלים בגובה הפירמידה, מחלקים את המכפלה המתקבלת ב. שְׁלוֹשָׁה.

ניתן לחשב את נפח הפירמידה באמצעות פרמטרים אחרים:

• כשליש מהמכפלה של רדיוס הכדור החתום בפירמידה ושטח פני השטח הכולל שלו;

• כשני שלישים מהמכפלה של המרחק בין שני קצוות חוצים שנלקחו באופן שרירותי לבין שטח המקבילית היוצר את נקודות האמצע של ארבעת הקצוות הנותרים.

נפח הפירמידה מחושב בפשטות גם במקרה שגובהה עולה בקנה אחד עם אחד מקצוות הצד, כלומר במקרה של פירמידה מלבנית.

אם כבר מדברים על פירמידות, אי אפשר להתעלם מהפירמידות הקטומות שמתקבלות על ידי חיתוך הפירמידה במישור מקביל לבסיס. הנפח שלהם כמעט שווה להפרש בין הנפחים של כל הפירמידה לחלק העליון החתוך.

הכרך הראשון של הפירמידה, אם כי לא ממש בו צורה מודרנית, לעומת זאת, שווה ל-1/3 מנפח הפריזמה המוכרת לנו, נמצא על ידי דמוקריטוס. ארכימדס כינה את שיטת הספירה שלו "ללא הוכחה", שכן דמוקריטוס התקרב לפירמידה כדמות המורכבת מלוחות דקים ודומים לאין שיעור.

אלגברה וקטורית "התייחסה" גם לשאלת מציאת נפח הפירמידה, תוך שימוש בקואורדינטות של קודקודיה לשם כך. פירמידה שנבנתה על טרויקה וקטורים a,b,c, שווה לשישית מהמודלוס של המכפלה המעורבת של הוקטורים הנתונים.

כאן ננתח דוגמאות הקשורות למושג נפח. כדי לפתור משימות כאלה, עליך לדעת את הנוסחה לנפח הפירמידה:

ס

h - גובה הפירמידה

הבסיס יכול להיות כל מצולע. אבל ברוב המשימות בבחינה, התנאי, ככלל, הוא על הפירמידות הנכונות. הרשו לי להזכיר לכם את אחד המאפיינים שלו:

החלק העליון של פירמידה רגילה מוקרן למרכז הבסיס שלה

תסתכל על ההשלכה של הפירמידות המשולשות, המרובעות והמשושים הרגילות (מבט למעלה):

אפשר בבלוג, שם טופלו המשימות הקשורות למציאת נפח הפירמידה.שקול את המשימות:

27087. מצא את נפחה של פירמידה משולשת רגילה שצלעות הבסיס שלה שוות ל-1 וגובהה שווה לשורש שלוש.

ס- שטח בסיס הפירמידה

ח- גובה הפירמידה

מצא את השטח של בסיס הפירמידה, זהו משולש רגיל. אנו משתמשים בנוסחה - שטח המשולש שווה למחצית המכפלה של צלעות סמוכות בסינוס של הזווית ביניהן, כלומר:

תשובה: 0.25

27088. מצא את הגובה של פירמידה משולשת רגילה עם צלעות הבסיס שוות ל-2 ונפחה שווה לשורש של שלוש.

מושגים כמו גובה הפירמידה ומאפייני הבסיס שלה קשורים בנוסחת הנפח:

ס- שטח בסיס הפירמידה

ח- גובה הפירמידה

אנחנו יודעים את הנפח עצמו, אנחנו יכולים למצוא את שטח הבסיס, מכיוון שצלעות המשולש, שהוא הבסיס, ידועות. הכרת הערכים הללו, נוכל למצוא בקלות את הגובה.

כדי למצוא את שטח הבסיס, אנו משתמשים בנוסחה - שטח המשולש שווה למחצית המכפלה של צלעות סמוכות בסינוס של הזווית ביניהן, כלומר:

לפיכך, על ידי החלפת ערכים אלה בנוסחת הנפח, נוכל לחשב את גובה הפירמידה:

הגובה הוא שלוש.

תשובה: 3

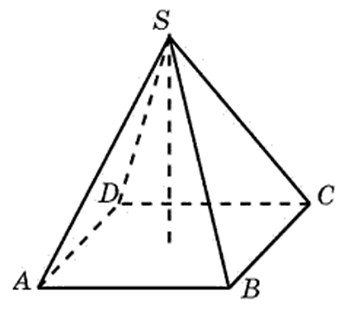
27109. בפירמידה מרובעת רגילה, הגובה הוא 6, קצה הצד הוא 10. מצא את הנפח שלה.

נפח הפירמידה מחושב לפי הנוסחה:

ס- שטח בסיס הפירמידה

ח- גובה הפירמידה

אנחנו יודעים את הגובה. אתה צריך למצוא את השטח של הבסיס. הרשו לי להזכיר לכם שחלקה העליון של פירמידה רגילה מוקרן למרכז הבסיס שלה. הבסיס של פירמידה מרובעת רגילה הוא ריבוע. אנחנו יכולים למצוא את האלכסון שלו. שקול משולש ישר זווית (מודגש בכחול):

הקטע המחבר את מרכז הריבוע עם נקודה B הוא רגל, השווה למחצית האלכסון של הריבוע. נוכל לחשב רגל זו באמצעות משפט פיתגורס:

אז BD = 16. חשב את שטח הריבוע באמצעות נוסחת השטח המרובע:

לָכֵן:

לפיכך, נפח הפירמידה הוא:

תשובה: 256

27178. בפירמידה מרובעת רגילה, הגובה הוא 12, הנפח הוא 200. מצא את קצה הצד של הפירמידה הזו.

גובה הפירמידה ונפחה ידועים ולכן נוכל למצוא את שטח הריבוע שהוא הבסיס. לדעת את השטח של ריבוע, נוכל למצוא את האלכסון שלו. יתר על כן, לאחר שקלטנו משולש ישר זווית, באמצעות משפט פיתגורס, אנו מחשבים את קצה הצד:

מצא את שטח הריבוע (בסיס הפירמידה):

חשב את האלכסון של הריבוע. מכיוון ששטחו 50, אז הצלע תהיה שווה לשורש חמישים, ולפי משפט פיתגורס:

הנקודה O מחלקת את האלכסון BD לשניים, כך שהרגל של המשולש הישר זווית OB = 5.

לפיכך, נוכל לחשב למה שווה קצה הצד של הפירמידה:

תשובה: 13

245353. מצא את נפח הפירמידה המוצגת באיור. בסיסו הוא מצולע שצלעותיו הסמוכות מאונכות, ואחד מקצוות הצד מאונך למישור הבסיס ושווה ל-3.

כפי שנאמר שוב ושוב - נפח הפירמידה מחושב לפי הנוסחה:

ס- שטח בסיס הפירמידה

ח- גובה הפירמידה

קצה הצד המאונך לבסיס הוא שלוש, כלומר גובה הפירמידה הוא שלושה. בסיס הפירמידה הוא מצולע ששטחו הוא:

לכן:

תשובה: 27

27086. בסיס הפירמידה הוא מלבן עם צלעות 3 ו-4. נפחו הוא 16. מצא את גובה הפירמידה הזו.

הַגדָרָה. פנים צדדיות- זהו משולש שבו זווית אחת נמצאת בראש הפירמידה, והצד הנגדי שלה חופף לצלע הבסיס (מצולע).

הַגדָרָה. צלעות צדהם הצדדים הנפוצים של פני הצד. לפירמידה יש ​​כמה קצוות כמו שיש פינות במצולע.

הַגדָרָה. גובה הפירמידההוא ניצב שנפל מלמעלה לבסיס הפירמידה.

הַגדָרָה. אפוטם- זהו הניצב של פני הצד של הפירמידה, מונמך מראש הפירמידה לצד הבסיס.

הַגדָרָה. חתך אלכסוני- זהו קטע של הפירמידה על ידי מישור העובר בראש הפירמידה ובאלכסון של הבסיס.

הַגדָרָה. פירמידה נכונה- זוהי פירמידה שבה הבסיס הוא מצולע רגיל, והגובה יורד למרכז הבסיס.

נפח ושטח הפנים של הפירמידה

נוּסחָה. נפח פירמידהדרך שטח בסיס וגובה:

מאפייני פירמידה

אם כל קצוות הצדדיים שווים, אז ניתן לתחום מעגל סביב בסיס הפירמידה, ומרכז הבסיס חופף למרכז המעגל. כמו כן, האנך שנפל מלמעלה עובר דרך מרכז הבסיס (עיגול).

אם כל הצלעות הצדדיות שוות, אז הן נוטות למישור הבסיס באותן זוויות.

הצלעות הרוחביות שוות כאשר הן יוצרות זוויות שוות עם מישור הבסיס, או אם ניתן לתאר עיגול סביב בסיס הפירמידה.

אם פני הצד נוטים למישור הבסיס בזווית אחת, אז ניתן לרשום מעגל בבסיס הפירמידה, וחלק העליון של הפירמידה מוקרן למרכזה.

אם פני הצדדיים נוטים למישור הבסיס בזווית אחת, אזי האפוטמים של פני הצדדיים שווים.

מאפיינים של פירמידה רגילה

1. החלק העליון של הפירמידה נמצא במרחק שווה מכל פינות הבסיס.

2. כל הקצוות הצדדיים שווים.

3. כל הצלעות הצדדיות נוטות באותן זוויות לבסיס.

4. אפוטמים של כל פני הצד שווים.

5. השטחים של כל פני הצד שווים.

6. לכל הפנים יש את אותן זוויות דיהדרליות (שטוחות).

7. ניתן לתאר כדור סביב הפירמידה. מרכז הכדור המתואר יהיה נקודת החיתוך של הניצבים העוברים באמצע הקצוות.

8. ניתן לרשום כדור בפירמידה. מרכז הכדור הכתוב יהיה נקודת החיתוך של חצויים הנובעים מהזווית שבין הקצה לבסיס.

9. אם מרכז הכדור הכתוב חופף למרכז הכדור המוקף, אזי סכום הזוויות השטוחות בקודקוד שווה ל-π או להיפך, זווית אחת שווה ל-π / n, כאשר n הוא המספר של זוויות בבסיס הפירמידה.

החיבור של הפירמידה עם הכדור

ניתן לתאר כדור סביב הפירמידה כאשר בבסיס הפירמידה שוכן פולידרון שסביבו ניתן לתאר עיגול (תנאי הכרחי ומספיק). מרכז הכדור יהיה נקודת החיתוך של מישורים העוברים בניצב דרך נקודות האמצע של הקצוות הצדדיים של הפירמידה.

תמיד אפשר לתאר כדור סביב כל פירמידה משולשת או רגילה.

ניתן לרשום כדור בפירמידה אם המישורים החצייים של הזוויות הדו-הדרליות הפנימיות של הפירמידה מצטלבים בנקודה אחת (תנאי הכרחי ומספיק). נקודה זו תהיה מרכז הכדור.

החיבור של הפירמידה עם החרוט

חרוט נקרא חרוט בפירמידה אם הקודקודים שלהם עולים בקנה אחד ובסיס החרוט רשום בבסיס הפירמידה.

ניתן לרשום חרוט בפירמידה אם המושגים של הפירמידה שווים.

אומרים שחרוט מוקף סביב פירמידה אם הקודקודים שלהם עולים בקנה אחד ובסיס החרוט מוקף סביב בסיס הפירמידה.

ניתן לתאר חרוט סביב פירמידה אם כל הקצוות הצדדיים של הפירמידה שווים זה לזה.

חיבור של פירמידה עם גליל

אומרים שפירמידה כתובה בגליל אם החלק העליון של הפירמידה מונח על בסיס אחד של הגליל, ובסיס הפירמידה רשום בבסיס אחר של הגליל.

ניתן לתחום גליל סביב פירמידה אם ניתן לתחום מעגל סביב בסיס הפירמידה.

הַגדָרָה. פירמידה קטומה (פריזמה פירמידלית)- זהו פולידרון שנמצא בין בסיס הפירמידה למישור חתך המקביל לבסיס. לפיכך לפירמידה יש ​​בסיס גדול ובסיס קטן יותר שדומה לגדול יותר. פני הצד הם טרפזים.

הַגדָרָה. פירמידה משולשת (טטרהדרון)- זוהי פירמידה שבה שלושה פנים והבסיס הם משולשים שרירותיים.

לטטרהדרון יש ארבעה פנים וארבעה קודקודים ושישה קצוות, כאשר לכל שני קצוות אין קודקודים משותפים אך אינם נוגעים.

כל קודקוד מורכב משלושה פנים וקצוות שנוצרים זווית תלת-תדרלית.

הקטע המחבר את קודקוד הטטרהדרון עם מרכז הפנים הנגדי נקרא החציון של הטטרהדרון(GM).

בימדיהנקרא קטע המחבר בין נקודות האמצע של קצוות מנוגדים שאינם נוגעים (KL).

כל הבימדיאנים והחציונים של טטרהדרון מצטלבים בנקודה אחת (S). במקרה זה, הבימדיאנים מחולקים לשניים, והחציונים ביחס של 3: 1 החל מלמעלה.

הַגדָרָה. פירמידה משופעתהיא פירמידה שבה אחד הקצוות יוצר זווית קהה (β) עם הבסיס.

הַגדָרָה. פירמידה מלבניתהיא פירמידה שבה אחד מפנים הצדדיות מאונך לבסיס.

הַגדָרָה. פירמידה חריפה בזוויתהיא פירמידה שבה האפוטם הוא יותר ממחצית אורך דופן הבסיס.

הַגדָרָה. פירמידה קהההיא פירמידה שבה האפוטם קטן ממחצית אורך דופן הבסיס.

הַגדָרָה. טטרהדרון רגילטטרהדרון שארבעת פניו הם משולשים שווי צלעות. זהו אחד מחמישה מצולעים רגילים. בטטרהדרון רגיל, כל הזוויות הדו-הדרליות (בין הפנים) והזוויות התלת-הדרליות (בקודקוד) שוות.

הַגדָרָה. טטרהדרון מלבנינקרא טטרהדרון שיש לו זווית ישרה בין שלושה קצוות בקודקוד (הקצוות מאונכים). נוצרות שלוש פרצופים זווית מלבנית משולשתוהקצוות הם משולשים ישרים, והבסיס הוא משולש שרירותי. ההטבה של כל פרצוף שווה למחצית הצד של הבסיס שעליו נופל האפוטם.

הַגדָרָה. טטרהדר איזוהדרליתטטרהדרון נקרא שבו פני הצד שווים זה לזה, והבסיס הוא משולש רגיל. פניו של טטרהדר כזה הם משולשים שווה שוקיים.

הַגדָרָה. טטרהדרון אורתוצנטרינקרא טטרהדרון שבו כל הגבהים (המאונכים) שיורדים מלמעלה אל הפנים הנגדי מצטלבים בנקודה אחת.

הַגדָרָה. פירמידת כוכביםפולידרון שבסיסו הוא כוכב נקרא.

הַגדָרָה. ביפירמידה- פולידרון המורכב משתי פירמידות שונות (ניתן גם לחתוך פירמידות) שיש מכנה משותף, והקודקודים שוכנים בצדדים מנוגדים של מישור הבסיס.

אחת הדמויות הנפחיות הפשוטות ביותר היא פירמידה משולשת, שכן היא מורכבת ממספר הפרצופים הקטן ביותר שמהם ניתן ליצור דמות בחלל. במאמר זה נשקול נוסחאות שבאמצעותן ניתן למצוא את נפח הפירמידה הרגילה משולשת.

פירמידה משולשת

לפי הגדרה נפוצהפירמידה היא מצולע, שכל קודקודיו מחוברים לנקודה אחת שאינה ממוקמת במישור המצולע הזה. אם האחרון הוא משולש, אז כל הדמות נקראת פירמידה משולשת.

הפירמידה הנחשבת מורכבת מבסיס (משולש) ומשלושה פני צד (משולשים). הנקודה שבה מחוברים שלושת פני הצד נקראת קודקוד הדמות. האנך שירד לבסיס מקודקוד זה הוא גובה הפירמידה. אם נקודת החיתוך של הניצב עם הבסיס עולה בקנה אחד עם נקודת החיתוך של חציוני המשולש בבסיס, אז הם מדברים על פירמידה רגילה. אחרת, זה יהיה משופע.

כאמור, הבסיס של פירמידה משולשת יכול להיות משולש סוג כללי. עם זאת, אם היא שווה צלעות, והפירמידה עצמה ישרה, אז הם מדברים על הדמות התלת מימדית הנכונה.

לכל אחד יש 4 פנים, 6 קצוות ו-4 קודקודים. אם האורכים של כל הקצוות שווים, אז דמות כזו נקראת טטרהדרון.

סוג כללי

לפני שכותבים פירמידה משולשת רגילה, אנו נותנים ביטוי לכך כמות פיסיתלפירמידה כללית. ביטוי זה נראה כך:

כאן S o הוא שטח הבסיס, h הוא גובה הדמות. שוויון זה יהיה תקף עבור כל סוג של בסיס של מצולע הפירמידה, כמו גם עבור החרוט. אם בבסיס יש משולש עם אורך הצלע a וגובה h o מונמך אליו, אזי הנוסחה לנפח תיכתב כך:

נוסחאות לנפח של פירמידה משולשת רגילה

למשולש יש משולש שווה צלעות בבסיס. ידוע שגובה המשולש הזה קשור לאורך הצלע שלו בשוויון:

החלפת ביטוי זה בנוסחה לנפח של פירמידה משולשת, שנכתבה בפסקה הקודמת, נקבל:

V = 1/6*a*h o *h = √3/12*a 2 *h.

הנפח של פירמידה רגילה עם בסיס משולש הוא פונקציה של אורך צלע הבסיס וגובה הדמות.

מכיוון שניתן לרשום כל מצולע רגיל במעגל שהרדיוס שלו קובע באופן ייחודי את אורך הצלע של המצולע, אז ניתן לכתוב את הנוסחה הזו במונחים של הרדיוס r המתאים:

קל להשיג נוסחה זו מהקודמת, בהתחשב בכך שרדיוס r של המעגל המוקף לאורך הצלע a של המשולש נקבע על ידי הביטוי:

המשימה של קביעת נפח טטרהדרון

הבה נראה כיצד להשתמש בנוסחאות לעיל בפתרון בעיות גיאומטריה ספציפיות.

ידוע שלטטרהדרון יש אורך קצה של 7 ס"מ. מצא את הנפח של פירמידה-טטרהדרון משולש רגיל.

נזכיר כי טטרהדרון היא פירמידה משולשת רגילה שבה כל הבסיסים שווים זה לזה. כדי להשתמש בנוסחה לנפח של פירמידה משולשת רגילה, עליך לחשב שתי כמויות:

• אורך הצלע של המשולש;
• גובה הדמות.

הערך הראשון ידוע ממצב הבעיה:

כדי לקבוע את הגובה, שקול את הדמות המוצגת באיור.

המשולש המסומן ABC הוא משולש ישר זווית כאשר הזווית ABC היא 90o. צד AC הוא התחתון, שאורכו הוא a. על ידי נימוק גיאומטרי פשוט, ניתן להראות שלצלע BC יש אורך:

שימו לב שאורך BC הוא רדיוס המעגל המוקף סביב המשולש.

h \u003d AB \u003d √ (AC 2 - BC 2) \u003d √ (a 2 - a 2/3) \u003d a * √ (2/3).

כעת אתה יכול להחליף את h ו-a בנוסחה המתאימה לנפח:

V = √3/12*a 2 *a*√(2/3) = √2/12*a 3 .

לפיכך, קיבלנו את הנוסחה לנפח של טטרהדרון. ניתן לראות שהנפח תלוי רק באורך הצלע. אם נחליף את הערך ממצב הבעיה בביטוי, נקבל את התשובה:

V \u003d √2 / 12 * 7 3 ≈ 40.42 ס"מ 3.

אם נשווה את הערך הזה לנפח של קובייה בעלת אותו קצה, נקבל שנפחו של טטרהדרון קטן פי 8.5. זה מצביע על כך שהטטרהדרון הוא דמות קומפקטית, שמתממשת בכמה חומרים טבעיים. לדוגמה, מולקולת המתאן היא טטרהדרלית, וכל אטום פחמן ביהלום מחובר לארבעה אטומים אחרים ליצירת טטרהדרון.

בעיה בפירמידות הומתוטיות

בואו נפתור בעיה גיאומטרית אחת מוזרה. נניח שקיימת פירמידה רגילה משולשת בעלת נפח כלשהו V 1 . בכמה פעמים יש להקטין את גודל הדמות הזו כדי לקבל פירמידה הומוטטית לה בנפח הקטן פי שלושה מהמקורי?

בואו נתחיל לפתור את הבעיה על ידי כתיבת הנוסחה של הפירמידה הרגילה המקורית:

V 1 \u003d √3 / 12 * a 1 2 * h 1.

אפשר לקבל את נפח הדמות הנדרשת ממצב הבעיה על ידי הכפלת הפרמטרים שלה במקדם k. יש לנו:

V 2 = √3/12*k 2 *a 1 2 *k*h 1 = k 3 *V 1.

מכיוון שהיחס בין נפחי הדמויות ידוע מהתנאי, נקבל את הערך של מקדם k:

k \u003d ∛ (V 2 / V 1) \u003d ∛ (1/3) ≈ 0.693.

שימו לב שהיינו מקבלים ערך דומה של מקדם k עבור סוג שרירותי של פירמידה, ולא רק עבור משולש רגיל.