סכום הלוגריתמים לאותו בסיס. לוגריתם של כלל הפעולה עם לוגריתמים

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

בוא נסביר את זה יותר קל. לדוגמה, \(\log_(2)(8)\) שווה לעוצמה \(2\) יש להעלות ל כדי לקבל \(8\). מכאן ברור ש\(\log_(2)(8)=3\).

דוגמאות:		\(\log_(5)(25)=2\)		כי \(5^(2)=25\)
		\(\log_(3)(81)=4\)		כי \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		כי \(2^(-5)=\)\(\frac(1)(32)\)

טיעון ובסיס הלוגריתם

לכל לוגריתם יש את ה"אנטומיה" הבאה:

הטיעון של הלוגריתם נכתב בדרך כלל ברמתו, והבסיס נכתב בכתב משנה קרוב יותר לסימן הלוגריתם. והערך הזה נקרא כך: "הלוגריתם של עשרים וחמש עד הבסיס של חמש".

איך מחשבים את הלוגריתם?

כדי לחשב את הלוגריתם, עליך לענות על השאלה: באיזו מידה יש ​​להעלות את הבסיס כדי לקבל את הטיעון?

לדוגמה, חשב את הלוגריתם: א) \(\log_(4)(16)\) ב) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) ה) \(\log_(3)(\sqrt(3))\)

א) לאיזה כוח יש להעלות \(4\) כדי לקבל \(16\)? ברור שהשני. זו הסיבה:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

ג) לאיזה עוצמה יש להעלות את \(\sqrt(5)\) כדי לקבל \(1\)? ואיזו מידה הופכת כל מספר ליחידה? אפס, כמובן!

\(\log_(\sqrt(5))(1)=0\)

ד) לאיזה עוצמה יש להעלות את \(\sqrt(7)\) כדי לקבל \(\sqrt(7)\)? בראשון - כל מספר במעלה הראשונה שווה לעצמו.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

ה) לאיזה כוח יש להעלות את \(3\) כדי לקבל \(\sqrt(3)\)? מתוך אנו יודעים שזה חזקת שבר, ולכן השורש הריבועי הוא חזקת \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

דוגמא : חשב את הלוגריתם \(\log_(4\sqrt(2))(8)\)

פִּתָרוֹן :

\(\log_(4\sqrt(2))(8)=x\)		אנחנו צריכים למצוא את הערך של הלוגריתם, בואו נסמן אותו כ-x. כעת נשתמש בהגדרה של הלוגריתם: \(\log_(a)(c)=b\) \(\Leftrightarrow\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		מה מקשר את \(4\sqrt(2)\) ו-\(8\)? שניים, כי שני המספרים יכולים להיות מיוצגים על ידי שניים: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		בצד שמאל, אנו משתמשים במאפייני התואר: \(a^(m)\cdot a^(n)=a^(m+n)\) ו-\((a^(m))^(n)=a ^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		הבסיסים שווים, אנו ממשיכים לשוויון האינדיקטורים
\(\frac(5x)(2)\) \(=3\)		הכפל את שני הצדדים של המשוואה ב-\(\frac(2)(5)\)
		השורש המתקבל הוא הערך של הלוגריתם

תשובה : \(\log_(4\sqrt(2))(8)=1,2\)

מדוע הומצא הלוגריתם?

כדי להבין זאת, נפתור את המשוואה: \(3^(x)=9\). פשוט התאם את \(x\) כדי לגרום לשוויון לעבוד. כמובן, \(x=2\).

כעת פתרו את המשוואה: \(3^(x)=8\) למה שווה x? זו הנקודה.

הגאוני ביותר יגיד: "X הוא קצת פחות משניים". איך בדיוק צריך לכתוב את המספר הזה? כדי לענות על השאלה הזו, הם המציאו את הלוגריתם. בזכותו ניתן לכתוב את התשובה כאן כ-\(x=\log_(3)(8)\).

אני רוצה להדגיש כי \(\log_(3)(8)\), כמו גם כל לוגריתם הוא רק מספר. כן, זה נראה יוצא דופן, אבל הוא קצר. כי אם היינו רוצים לכתוב את זה בתור עשרוני, זה היה נראה כך: \(1.892789260714.....\)

דוגמא : פתרו את המשוואה \(4^(5x-4)=10\)

פִּתָרוֹן :

\(4^(5x-4)=10\)		לא ניתן לצמצם את \(4^(5x-4)\) ו-\(10\) לאותו בסיס. אז כאן אתה לא יכול בלי הלוגריתם. בואו נשתמש בהגדרה של הלוגריתם: \(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		הפוך את המשוואה כך ש-x יהיה בצד שמאל
\(5x-4=\log_(4)(10)\)		לפנינו. הזז את \(4\) ימינה. ואל תפחדו מהלוגריתם, התייחסו אליו כאל מספר רגיל.
\(5x=\log_(4)(10)+4\)		מחלקים את המשוואה ב-5
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		הנה השורש שלנו. כן, זה נראה יוצא דופן, אבל התשובה לא נבחרה.

תשובה : \(\frac(\log_(4)(10)+4)(5)\)

לוגריתמים עשרוניים וטבעיים

כפי שנאמר בהגדרת הלוגריתם, הבסיס שלו יכול להיות כל מספר חיובי מלבד אחד \((a>0, a\neq1)\). ובין כל הבסיסים האפשריים, ישנם שניים המתרחשים לעתים קרובות כל כך עד שהומצא איתם סימון קצר מיוחד ללוגריתמים:

לוגריתם טבעי: לוגריתם שהבסיס שלו הוא מספר אוילר \(e\) (שווה ל-\(2.7182818...\) בקירוב), והלוגריתם נכתב כ-\(\ln(a)\).

זה, \(\ln(a)\) זהה ל-\(\log_(e)(a)\)

לוגריתם עשרוני: לוגריתם שהבסיס שלו הוא 10 נכתב \(\lg(a)\).

זה, \(\lg(a)\) זהה ל-\(\log_(10)(a)\), כאשר \(a\) הוא מספר כלשהו.

זהות לוגריתמית בסיסית

ללוגריתמים יש תכונות רבות. אחד מהם נקרא "זהות לוגריתמית בסיסית" ונראה כך:

\(a^(\log_(a)(c))=c\)

מאפיין זה נובע ישירות מההגדרה. בואו נראה איך נוצרה הנוסחה הזו.

זכור את ההגדרה הקצרה של הלוגריתם:

אם \(a^(b)=c\), אז \(\log_(a)(c)=b\)

כלומר, \(b\) זהה ל-\(\log_(a)(c)\). אז נוכל לכתוב \(\log_(a)(c)\) במקום \(b\) בנוסחה \(a^(b)=c\) . התברר \(a^(\log_(a)(c))=c\) - הזהות הלוגריתמית העיקרית.

אתה יכול למצוא את שאר המאפיינים של לוגריתמים. בעזרתם, אתה יכול לפשט ולחשב את ערכי הביטויים עם לוגריתמים, שקשה לחשב ישירות.

דוגמא : מצא את הערך של הביטוי \(36^(\log_(6)(5))\)

פִּתָרוֹן :

תשובה : \(25\)

איך כותבים מספר כלוגריתם?

כפי שהוזכר לעיל, כל לוגריתם הוא רק מספר. גם ההיפך נכון: ניתן לכתוב כל מספר כלוגריתם. לדוגמה, אנו יודעים ש-\(\log_(2)(4)\) שווה לשניים. אז אתה יכול לכתוב \(\log_(2)(4)\) במקום שניים.

אבל \(\log_(3)(9)\) שווה גם ל-\(2\), אז אתה יכול גם לכתוב \(2=\log_(3)(9)\) . באופן דומה עם \(\log_(5)(25)\), ועם \(\log_(9)(81)\), וכו'. כלומר, מסתבר

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

לפיכך, אם נצטרך, נוכל לכתוב את השניים כלוגריתם עם כל בסיס בכל מקום (אפילו במשוואה, אפילו בביטוי, אפילו באי שוויון) - אנחנו פשוט כותבים את הבסיס בריבוע כארגומנט.

זה אותו דבר עם משולש - אפשר לכתוב אותו כ-\(\log_(2)(8)\), או כ-\(\log_(3)(27)\), או כ-\(\log_(4)( 64) \) ... כאן אנו כותבים את הבסיס בקובייה כארגומנט:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

ועם ארבעה:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

ועם מינוס אחד:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\)\(...\)

ועם שליש:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

כל מספר \(a\) יכול להיות מיוצג כלוגריתם עם בסיס \(b\): \(a=\log_(b)(b^(a))\)

דוגמא : מצא את הערך של ביטוי \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

פִּתָרוֹן :

תשובה : \(1\)

הוראה

רשום את הביטוי הלוגריתמי הנתון. אם הביטוי משתמש בלוגריתם של 10, הסימון שלו מתקצר ונראה כך: lg b הוא הלוגריתם העשרוני. אם ללוגריתם יש את המספר e כבסיס, אז הביטוי נכתב: ln b הוא הלוגריתם הטבעי. מובן שהתוצאה של כל היא החזקה אליה יש להעלות את מספר הבסיס כדי לקבל את המספר b.

כשמוצאים את הסכום של שתי פונקציות, אתה רק צריך להבדיל ביניהן אחת אחת, ולהוסיף את התוצאות: (u+v)" = u"+v";

כשמוצאים את הנגזרת של המכפלה של שתי פונקציות, יש צורך להכפיל את הנגזרת של הפונקציה הראשונה בשנייה ולהוסיף את הנגזרת של הפונקציה השנייה, כפול הפונקציה הראשונה: (u*v)" = u"* v+v"*u;

על מנת למצוא את הנגזרת של המנה של שתי פונקציות, יש צורך, ממכפלת הנגזרת של הדיבידנד כפול פונקציית המחלק, להחסיר את מכפלת הנגזרת של המחלק כפולה בפונקציית המחלק, ולחלק כל זה לפי פונקציית המחלק בריבוע. (u/v)" = (u"*v-v"*u)/v^2;

אם ניתנת פונקציה מורכבת, אז יש צורך להכפיל את הנגזרת של הפונקציה הפנימית ואת הנגזרת של החיצונית. תן y=u(v(x)), ואז y"(x)=y"(u)*v"(x).

באמצעות המתקבל לעיל, אתה יכול להבדיל כמעט כל פונקציה. אז בואו נסתכל על כמה דוגמאות:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *איקס));
יש גם משימות לחישוב הנגזרת בנקודה. תן את הפונקציה y=e^(x^2+6x+5), אתה צריך למצוא את הערך של הפונקציה בנקודה x=1.
1) מצא את הנגזרת של הפונקציה: y"=e^(x^2-6x+5)*(2*x +6).

2) חשב את הערך של הפונקציה בנקודה הנתונה y"(1)=8*e^0=8

סרטונים קשורים

עצה שימושית

למד את טבלת הנגזרות היסודיות. זה יחסוך הרבה זמן.

מקורות:

• נגזרת קבועה

אז מה ההבדל בין משוואה לא רציונלית לרציונלית? אם המשתנה הלא ידוע נמצא מתחת לסימן השורש הריבועי, אז המשוואה נחשבת לא רציונלית.

הוראה

השיטה העיקרית לפתרון משוואות כאלה היא שיטת העלאת שני החלקים משוואותלתוך ריבוע. למרות זאת. זה טבעי, הצעד הראשון הוא להיפטר מהשלט. מבחינה טכנית, שיטה זו אינה קשה, אך לפעמים היא עלולה להוביל לצרות. לדוגמה, המשוואה v(2x-5)=v(4x-7). על ידי ריבוע שני הצדדים, אתה מקבל 2x-5=4x-7. משוואה כזו לא קשה לפתרון; x=1. אבל המספר 1 לא יינתן משוואות. למה? תחליף את היחידה במשוואה במקום בערך x. והצד הימני והשמאלי יכילו ביטויים לא הגיוניים, כלומר. ערך כזה אינו תקף לשורש ריבועי. לכן, 1 הוא שורש חיצוני, ולכן למשוואה זו אין שורשים.

אז, המשוואה האי-רציונלית נפתרת באמצעות השיטה של ​​ריבוע שני חלקיה. ולאחר שפתרו את המשוואה, יש צורך לחתוך שורשים זרים. כדי לעשות זאת, החלף את השורשים שנמצאו במשוואה המקורית.

שקול עוד אחד.
2x+vx-3=0
כמובן שניתן לפתור את המשוואה הזו באמצעות אותה משוואה כמו הקודמת. תרכובות העברה משוואות, שאין להם שורש ריבועי, לצד ימין ואז משתמשים בשיטת הריבוע. לפתור את המשוואה הרציונלית שהתקבלה ואת השורשים. אבל אחר, אלגנטי יותר. הזן משתנה חדש; vx=y. בהתאם, תקבל משוואה כמו 2y2+y-3=0. זו המשוואה הריבועית הרגילה. מצא את שורשיו; y1=1 ו-y2=-3/2. לאחר מכן, פתור שניים משוואות vx=1; vx \u003d -3/2. למשוואה השנייה אין שורשים, מהראשונה נמצא ש-x=1. אל תשכח את הצורך לבדוק את השורשים.

פתרון זהויות הוא די קל. זה דורש ביצוע טרנספורמציות זהות עד להשגת המטרה. כך, בעזרת פעולות החשבון הפשוטות ביותר, המשימה תיפתר.

אתה תצטרך

• - עיתון;
• - עט.

הוראה

הטרנספורמציות הפשוטות ביותר מסוג זה הן הכפלות מקוצרות אלגבריות (כגון ריבוע הסכום (הפרש), הפרש הריבועים, הסכום (הפרש), קוביית הסכום (הפרש)). בנוסף, ישנן נוסחאות טריגונומטריות רבות שהן בעצם אותן זהויות.

ואכן, ריבוע הסכום של שני איברים שווה לריבוע של הראשון פלוס פעמיים המכפלה של הראשון והשני פלוס הריבוע של השני, כלומר (a+b)^2= (a+b) )(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

פשט את שניהם

עקרונות כלליים של פתרון

חזור מתוך ספר לימוד על ניתוח מתמטי או מתמטיקה גבוהה יותר, שהוא אינטגרל מובהק. כידוע, הפתרון של אינטגרל מוגדר הוא פונקציה שהנגזרת שלה תיתן אינטגרנד. פונקציה זו נקראת אנטי נגזרת. לפי עיקרון זה בנויים האינטגרלים הבסיסיים.
קבע לפי צורת האינטגרנד איזה מבין אינטגרלי הטבלה מתאים במקרה זה. לא תמיד ניתן לקבוע זאת מיד. לעתים קרובות, הצורה הטבלאית הופכת בולטת רק לאחר מספר טרנספורמציות כדי לפשט את האינטגרנד.

שיטת החלפה משתנה

אם האינטגרנד הוא פונקציה טריגונומטרית שהארגומנט שלה הוא פולינום כלשהו, ​​נסה להשתמש בשיטת שינוי המשתנים. לשם כך, החלף את הפולינום בארגומנט של האינטגרנד במשתנה חדש כלשהו. בהתבסס על היחס בין המשתנה החדש והישן, קבע את גבולות האינטגרציה החדשים. על ידי הבחנה של ביטוי זה, מצא דיפרנציאל חדש ב. לפיכך, תקבלו צורה חדשה של האינטגרל הישן, קרובה או אפילו מתאימה לכל טבלאי.

פתרון אינטגרלים מהסוג השני

אם האינטגרל הוא אינטגרל מהסוג השני, הצורה הווקטורית של האינטגרנד, אז תצטרך להשתמש בכללים למעבר מאינטגרלים אלו לסקלרים. כלל אחד כזה הוא יחס אוסטרוגרדסקי-גאוס. חוק זה מאפשר לעבור מזרימת הרוטור של פונקציה וקטורית כלשהי לאינטגרל משולש על פני הסטייה של שדה וקטור נתון.

החלפת גבולות האינטגרציה

לאחר מציאת הנגזרת האנטי-נגזרת, יש צורך להחליף את גבולות האינטגרציה. ראשית, החלף את הערך של הגבול העליון בביטוי עבור האנטי-נגזרת. תקבל מספר כלשהו. לאחר מכן, הפחיתו מהמספר המתקבל מספר נוסף, הגבול התחתון המתקבל לנגזרת האנטי. אם אחד מגבולות האינטגרציה הוא אינסוף, אז כאשר מחליפים אותו בפונקציה האנטי-נגזרת, יש צורך ללכת לגבול ולמצוא למה הביטוי נוטה.
אם האינטגרל הוא דו מימדי או תלת מימדי, אז תצטרכו לייצג את הגבולות הגיאומטריים של האינטגרל על מנת להבין כיצד לחשב את האינטגרל. ואכן, במקרה של, נניח, אינטגרל תלת מימדי, גבולות האינטגרציה יכולים להיות מישורים שלמים המגבילים את הנפח שיש לשלב.

הגדרה של לוגריתם

הלוגריתם של המספר b לבסיס a הוא המעריך אליו צריך להעלות את a כדי לקבל את b.

המספר הבמתמטיקה נהוג לציין את הגבול אליו נוטה הביטוי

מספר ההוא מספר לא רציונלי- מספר שאינו תואם לאחד, לא ניתן לבטא אותו במדויק לא כשלם או כשבר רַצִיוֹנָלִימספר.

מִכְתָב ה- האות הראשונה של מילה לטינית פטור- להתהדר, ומכאן השם במתמטיקה אקספוננציאלי- פונקציה מעריכית.

מספר הבשימוש נרחב במתמטיקה, ובכל המדעים, בדרך זו או אחרת תוך שימוש בחישובים מתמטיים לצרכיהם.

לוגריתמים. מאפיינים של לוגריתמים

הגדרה: לוגריתם הבסיס של מספר חיובי b הוא המעריך c אליו יש להעלות את המספר a כדי לקבל את המספר b.

זהות לוגריתמית בסיסית:

7) נוסחה למעבר לבסיס חדש:

lna = log e a, e ≈ 2.718…

משימות ומבחנים בנושא "לוגריתמים. מאפיינים של לוגריתמים»

• לוגריתמים - נושאים חשובים לחזרה על הבחינה במתמטיקה

כדי להשלים בהצלחה משימות בנושא זה, עליך לדעת את ההגדרה של הלוגריתם, את תכונות הלוגריתמים, את הזהות הלוגריתמית הבסיסית, את ההגדרות של לוגריתמים עשרוניים וטבעיים. סוגי המשימות העיקריים בנושא זה הם משימות לחישוב והמרת ביטויים לוגריתמיים. הבה נשקול את הפתרון שלהם על הדוגמאות הבאות.

פִּתָרוֹן:באמצעות המאפיינים של לוגריתמים, אנו מקבלים

פִּתָרוֹן:באמצעות המאפיינים של התואר, אנו מקבלים

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

תכונות לוגריתמים, ניסוחים והוכחות.

ללוגריתמים יש מספר תכונות אופייניות. במאמר זה ננתח את העיקר מאפיינים של לוגריתמים. כאן אנו נותנים את הניסוחים שלהם, רושמים את תכונות הלוגריתמים בצורה של נוסחאות, מציגים דוגמאות ליישום שלהם, וגם נותנים הוכחות לתכונות הלוגריתמים.

ניווט בדף.

מאפיינים בסיסיים של לוגריתמים, נוסחאות

כדי להקל על הזיכרון והשימוש, אנו מציגים תכונות בסיסיות של לוגריתמיםכרשימה של נוסחאות. בחלק הבא, אנו נותנים את הניסוחים שלהם, הוכחות, דוגמאות לשימוש והסברים נחוצים.

מאפיין יומן יחידה: רישום a 1=0 עבור כל a>0 , a≠1 .

הלוגריתם של מספר השווה לבסיס: log a a=1 עבור a>0 , a≠1 .

מאפיין לוגריתם של תואר בסיס: log a a p =p , כאשר a>0 , a≠1 ו-p הם כל מספר ממשי.

הלוגריתם של המכפלה של שני מספרים חיוביים: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
והמאפיין של הלוגריתם של המכפלה של n מספרים חיוביים: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 >0, …, xn >0 .

מאפיין לוגריתם פרטי: , כאשר a>0 , a≠1 , x>0 , y>0 .

לוגריתם של חזקה של מספר: log a b p =p log a |b| , כאשר a>0 , a≠1 , b ו-p הם מספרים כך שהדרגה של b p הגיונית ו-b p >0 .

תוֹצָאָה: , כאשר a>0 , a≠1 , n הוא מספר טבעי הגדול מאחד, b>0 .

מסקנה 1: , a>0 , a≠1 , b>0 , b≠1 .

מסקנה 2: , a>0 , a≠1 , b>0 , p ו- q הם מספרים ממשיים, q≠0 , בפרט, עבור b=a יש לנו .

הצהרות והוכחות לנכסים

אנו עוברים לניסוח ולהוכחה של המאפיינים הרשומים של לוגריתמים. כל תכונות הלוגריתמים מוכחות על בסיס הגדרת הלוגריתם והזהות הלוגריתמית הבסיסית הנובעת ממנו וכן תכונות התואר.

בוא נתחיל עם תכונות הלוגריתם של האחדות. הניסוח שלו הוא כדלקמן: הלוגריתם של האחדות שווה לאפס, כלומר, log a 1=0עבור כל a>0 , a≠1 . ההוכחה היא פשוטה: מכיוון ש-0 =1 עבור כל a המקיים את התנאים שלעיל a>0 ו-a≠1, אזי השוויון המוכח a 1=0 נובע מיד מהגדרת הלוגריתם.

בואו ניתן דוגמאות ליישום של המאפיין הנחשב: log 3 1=0 , lg1=0 ו- .

נעבור לנכס הבא: הלוגריתם של מספר השווה לבסיס שווה לאחד, זה, log a=1עבור a>0, a≠1. ואכן, מכיוון ש-1 =a עבור כל a, אז לפי הגדרת הלוגריתם log a a=1.

דוגמאות לשימוש בתכונה זו של לוגריתמים הן log 5 5=1 , log 5.6 5.6 ו-lne=1 .

הלוגריתם בחזקת מספר השווה לבסיס הלוגריתם שווה למעריך. מאפיין זה של הלוגריתם מתאים לנוסחה של הצורה log a a p =p, כאשר a>0 , a≠1 ו-p הוא כל מספר ממשי. מאפיין זה נובע ישירות מהגדרת הלוגריתם. שימו לב שהוא מאפשר לציין מיד את ערך הלוגריתם, אם אפשר לייצג את המספר מתחת לסימן הלוגריתם כדרגת בסיס, נדבר על כך יותר במאמר חישוב לוגריתמים.

לדוגמה, log 2 2 7 =7 , log10 -4 =-4 ו .

לוגריתם של מכפלת שני מספרים חיוביים x ו-y שווים למכפלת הלוגריתמים של המספרים האלה: log a (x y)=log a x+log a y, a>0 , a≠1 . הבה נוכיח את תכונת הלוגריתם של המוצר. בשל תכונות התואר a log a x + log a y =a log a x a log a y, ומכיוון שלפי הזהות הלוגריתמית הראשית a log a x =x ו-log a y =y, אז log a x a log a y =x y. לפיכך, log a x+log a y =x y, מכאן שהשוויון הנדרש בא בעקבות הגדרת הלוגריתם.

הבה נראה דוגמאות לשימוש בתכונה של הלוגריתם של המוצר: log 5 (2 3)=log 5 2+log 5 3 and .

ניתן להכליל את תכונת לוגריתם המכפלה למכפלה של מספר סופי n של מספרים חיוביים x 1 , x 2 , …, x n as log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. ניתן להוכיח שוויון זה בקלות בשיטת האינדוקציה המתמטית.

לדוגמה, ניתן להחליף את הלוגריתם הטבעי של מכפלה בסכום של שלושה לוגריתמים טבעיים של המספרים 4, e ו-.

לוגריתם של המנה של שני מספרים חיוביים x ו-y שווים להפרש בין הלוגריתמים של המספרים הללו. המאפיין של לוגריתם המנה מתאים לנוסחה של הצורה , כאשר a>0 , a≠1 , x ו- y הם כמה מספרים חיוביים. תקפותה של נוסחה זו מוכחת כמו הנוסחה ללוגריתם של המכפלה: מאז , אז לפי הגדרת הלוגריתם .

הנה דוגמה לשימוש בתכונה זו של הלוגריתם: .

בואו נעבור ל תכונת הלוגריתם של התואר. הלוגריתם של תואר שווה למכפלת המעריך וללוגריתם של מודול הבסיס של תואר זה. אנו כותבים תכונה זו של הלוגריתם של התואר בצורה של נוסחה: log a b p =p log a |b|, כאשר a>0 , a≠1 , b ו-p הם מספרים כך שהדרגה של b p הגיונית ו-b p >0 .

תחילה אנו מוכיחים תכונה זו עבור b חיובי. הזהות הלוגריתמית הבסיסית מאפשרת לנו לייצג את המספר b כ-log a b, ואז b p =(a log a b) p, והביטוי המתקבל, עקב תכונת הכוח, שווה ל-p log a b. אז אנחנו מגיעים לשוויון b p =a p log a b, שממנו, לפי הגדרת הלוגריתם, אנו מסיקים ש-log a b p =p log a b.

נותר להוכיח תכונה זו עבור b שלילית. כאן נציין שהביטוי log a b p עבור b שלילי הגיוני רק עבור אקספוננטים p (מכיוון שהערך של התואר b p חייב להיות גדול מאפס, אחרת הלוגריתם לא יהיה הגיוני), ובמקרה זה b p =|b| עמ' . ואז b p =|b| p =(a log a |b|) p =a p log a |b| , משם log a b p =p log a |b| .

לדוגמה, ו-ln(-3) 4 =4 ln|-3|=4 ln3 .

זה נובע מהנכס הקודם תכונת הלוגריתם מהשורש: הלוגריתם של שורש המעלה ה-n שווה למכפלת השבר 1/n והלוגריתם של ביטוי השורש, כלומר כאשר a>0, a≠1, n הוא מספר טבעי הגדול מאחד, b>0.

ההוכחה מבוססת על שוויון (ראה הגדרה של מעריך עם מעריך שבר), שתקף לכל b חיובי, ועל תכונת הלוגריתם של התואר: .

הנה דוגמה לשימוש במאפיין זה: .

עכשיו בואו נוכיח נוסחת המרה לבסיס החדש של הלוגריתםסוג . לשם כך, די להוכיח את תקפות יומן השוויון c b=log a b log c a . הזהות הלוגריתמית הבסיסית מאפשרת לנו לייצג את המספר b בתור log a b , ואז log c b=log c a log a b . נותר להשתמש בתכונה של הלוגריתם של התואר: log c a log a b = log a b log c a . לפיכך, מוכח השוויון log c b=log a b log c a, כלומר מוכחת גם הנוסחה למעבר לבסיס חדש של הלוגריתם .

הבה נראה כמה דוגמאות ליישום תכונה זו של לוגריתמים: ו .

הנוסחה למעבר לבסיס חדש מאפשרת לעבור לעבודה עם לוגריתמים בעלי בסיס "נוח". לדוגמה, ניתן להשתמש בו כדי לעבור ללוגריתמים טבעיים או עשרוניים, כך שתוכל לחשב את ערך הלוגריתם מטבלת לוגריתמים. הנוסחה למעבר לבסיס חדש של הלוגריתם מאפשרת במקרים מסוימים גם למצוא את הערך של לוגריתם נתון, כאשר הערכים של כמה לוגריתמים עם בסיסים אחרים ידועים.

לעתים קרובות נעשה שימוש במקרה מיוחד של נוסחת המעבר לבסיס חדש של הלוגריתם עבור c=b של הצורה. זה מראה שלוג a b ולוג b a הם מספרים הפוכים זה לזה. לדוגמה, .

הנוסחה משמשת גם לעתים קרובות, וזה נוח למציאת ערכי לוגריתם. כדי לאשר את דברינו, נראה כיצד מחושב ערך הלוגריתם של הטופס באמצעותו. יש לנו . כדי להוכיח את הנוסחה, די להשתמש בנוסחת המעבר לבסיס החדש של הלוגריתם a: .

נותר להוכיח את תכונות ההשוואה של לוגריתמים.

בוא נשתמש בשיטה ההפוכה. נניח שעבור a 1 >1, a 2 >1 ו-a 1 2 ועבור 0 1 log a 1 b≤log a 2 b נכון. לפי המאפיינים של לוגריתמים, אי-שוויון אלה יכולים להיכתב מחדש כ ו בהתאמה, ומהם נובע ש-log b a 1 ≤log b a 2 ו-log b a 1 ≥log b a 2, בהתאמה. לאחר מכן, לפי המאפיינים של חזקות עם אותם בסיסים, יש להתקיים השוויון b log b a 1 ≥b log b a 2 ו-b log b a 1 ≥b log b a 2, כלומר, a 1 ≥a 2. לפיכך, הגענו לסתירה לתנאי a 1 2 . זה משלים את ההוכחה.

מאפיינים בסיסיים של לוגריתמים

• חומרים לשיעור
• הורד את כל הנוסחאות

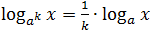
לוגריתמים, כמו כל מספר, ניתן להוסיף, לגרוע ולהמיר בכל דרך אפשרית. אבל מכיוון שהלוגריתמים אינם מספרים רגילים לגמרי, יש כאן חוקים שנקראים מאפיינים בסיסיים.

חוקים אלו חייבים להיות ידועים - לא ניתן לפתור בעיה לוגריתמית רצינית בלעדיהם. בנוסף, יש מעט מאוד מהם - הכל ניתן ללמוד ביום אחד. אז בואו נתחיל.

חיבור וחיסור של לוגריתמים

שקול שני לוגריתמים עם אותו בסיס: יומן a x ו- log a y . לאחר מכן ניתן להוסיף ולהחסיר אותם, ו:

אז, סכום הלוגריתמים שווה ללוגריתם של המכפלה, וההבדל הוא הלוגריתם של המנה. שימו לב: נקודת המפתח כאן היא - אותם נימוקים. אם הבסיסים שונים, הכללים האלה לא עובדים!

נוסחאות אלו יסייעו בחישוב הביטוי הלוגריתמי גם כאשר חלקיו הבודדים אינם נחשבים (ראה השיעור "מהו לוגריתם"). תסתכל על הדוגמאות - וראה:

משימה. מצא את הערך של הביטוי: log 6 4 + log 6 9.

מכיוון שהבסיסים של הלוגריתמים זהים, אנו משתמשים בנוסחת הסכום:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

משימה. מצא את הערך של הביטוי: log 2 48 − log 2 3.

הבסיסים זהים, אנו משתמשים בנוסחת ההבדל:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

משימה. מצא את הערך של הביטוי: log 3 135 − log 3 5.

שוב, הבסיסים זהים, אז יש לנו:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

כפי שניתן לראות, הביטויים המקוריים מורכבים מלוגריתמים "רעים", שאינם נחשבים בנפרד. אבל לאחר טרנספורמציות מסתבר מספרים נורמליים למדי. בדיקות רבות מבוססות על עובדה זו. כן, השליטה הזו - ביטויים דומים במלוא הרצינות (לפעמים - כמעט ללא שינויים) מוצעים בבחינה.

הסרת המעריך מהלוגריתם

עכשיו בואו נסבך מעט את המשימה. מה אם יש תואר בבסיס או בארגומנט של הלוגריתם? אז ניתן להוציא את המעריך של תואר זה מהסימן של הלוגריתם לפי הכללים הבאים:

• log a x n = n log a x ;
• 
• 

קל לראות שהכלל האחרון עוקב אחר השניים הראשונים שלהם. אבל עדיף בכל זאת לזכור - במקרים מסוימים זה יקטין משמעותית את כמות החישובים.

כמובן, כל הכללים האלה הגיוניים אם מתקיים הלוגריתם של ODZ: a > 0, a ≠ 1, x > 0. ועוד דבר: למד ליישם את כל הנוסחאות לא רק משמאל לימין, אלא גם להיפך, כלומר. אתה יכול להזין את המספרים לפני הסימן של הלוגריתם לתוך הלוגריתם עצמו. זה מה שנדרש לרוב.

משימה. מצא את הערך של הביטוי: log 7 49 6 .

בואו נפטר מהדרגה בטיעון לפי הנוסחה הראשונה:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

משימה. מצא את הערך של הביטוי:

[כיתוב תמונה]

שימו לב שהמכנה הוא לוגריתם שהבסיס והארגומנט שלו הם בחזקות מדויקות: 16 = 2 4 ; 49 = 72. יש לנו:

[כיתוב תמונה]

אני חושב שהדוגמה האחרונה דורשת הבהרה. לאן נעלמו הלוגריתמים? עד הרגע האחרון אנחנו עובדים רק עם המכנה. הם הציגו את הבסיס והטיעון של הלוגריתם שעומד שם בצורה של מעלות והוציאו את האינדיקטורים - הם קיבלו שבר של "שלוש קומות".

עכשיו בואו נסתכל על השבר העיקרי. למונה ולמכנה יש אותו מספר: log 2 7. מכיוון שלוג 2 7 ≠ 0, נוכל לצמצם את השבר - 2/4 יישאר במכנה. לפי כללי החשבון ניתן להעביר את הארבעה למונה, מה שנעשה. התוצאה היא התשובה: 2.

מעבר לקרן חדשה

כשדיברתי על הכללים לחיבור והפחתה של לוגריתמים, הדגשתי במיוחד שהם עובדים רק עם אותם בסיסים. מה אם הבסיסים שונים? מה אם הם לא חזקות מדויקות של אותו מספר?

נוסחאות למעבר לבסיס חדש באות לעזרה. אנו מנסחים אותם בצורה של משפט:

תנו ללוגריתם יומן x להינתן. אז עבור כל מספר c כך ש-c > 0 ו-c ≠ 1, השוויון נכון:

[כיתוב תמונה]

בפרט, אם נשים את c = x , נקבל:

[כיתוב תמונה]

מהנוסחה השנייה עולה שאפשר להחליף בין הבסיס לבין הטיעון של הלוגריתם, אבל במקרה זה הביטוי כולו "מתהפך", כלומר. הלוגריתם נמצא במכנה.

נוסחאות אלה נמצאות רק לעתים נדירות בביטויים מספריים רגילים. אפשר להעריך עד כמה הם נוחים רק כאשר פותרים משוואות ואי-שוויון לוגריתמיות.

עם זאת, ישנן משימות שלא ניתן לפתור כלל מלבד מעבר לקרן חדשה. בואו נשקול כמה כאלה:

משימה. מצא את הערך של הביטוי: log 5 16 log 2 25.

שימו לב שהארגומנטים של שני הלוגריתמים הם אקספוננטים מדויקים. הבה נוציא את האינדיקטורים: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

כעת נהפוך את הלוגריתם השני:

[כיתוב תמונה]

מכיוון שהמכפלה לא משתנה מתמורה של גורמים, הכפלנו בשלווה ארבע ושתיים, ואז הבנו את הלוגריתמים.

משימה. מצא את הערך של הביטוי: log 9 100 lg 3.

הבסיס והטיעון של הלוגריתם הראשון הם חזקות מדויקות. בואו נרשום את זה ונפטר מהאינדיקטורים:

[כיתוב תמונה]

עכשיו בואו נפטר מהלוגריתם העשרוני על ידי מעבר לבסיס חדש:

[כיתוב תמונה]

זהות לוגריתמית בסיסית

לעתים קרובות בתהליך הפתרון נדרש לייצג מספר כלוגריתם לבסיס נתון. במקרה זה, הנוסחאות יעזרו לנו:

1. n = log a a n

2. במקרה הראשון, המספר n הופך למעריך בארגומנט. המספר n יכול להיות כל דבר, כי זה רק הערך של הלוגריתם.

   הנוסחה השנייה היא למעשה הגדרה פרפרזה. זה נקרא הזהות הלוגריתמית הבסיסית.

   ואכן, מה יקרה אם המספר b יועלה לחזק כזה שהמספר b בחזקת זה נותן את המספר a? זה נכון: זה אותו מספר a . קרא שוב את הפסקה הזו בעיון - אנשים רבים "נתלים" בה.

   כמו נוסחאות המרת הבסיס החדשות, הזהות הלוגריתמית הבסיסית היא לפעמים הפתרון האפשרי היחיד.

   [כיתוב תמונה]

   שימו לב שלוג 25 64 = יומן 5 8 - פשוט קחו את הריבוע של הבסיס ואת הארגומנט של הלוגריתם. בהינתן הכללים להכפלת חזקות עם אותו בסיס, אנו מקבלים:

   [כיתוב תמונה]

   אם מישהו לא יודע, זו הייתה משימה אמיתית מבחינת המדינה המאוחדת 🙂

   יחידה לוגריתמית ואפס לוגריתמי

   לסיכום, אתן שתי זהויות שקשה לקרוא להן מאפיינים – אלא אלו השלכות מהגדרת הלוגריתם. הם נמצאים כל הזמן בבעיות ובאופן מפתיע יוצרים בעיות גם לתלמידים "מתקדמים".

   1. log a a = 1 היא היחידה הלוגריתמית. זכור אחת ולתמיד: הלוגריתם לכל בסיס a מאותו בסיס עצמו שווה לאחד.
   2. log a 1 = 0 הוא אפס לוגריתמי. הבסיס a יכול להיות כל דבר, אבל אם הארגומנט הוא אחד - הלוגריתם הוא אפס! כי 0 = 1 הוא תוצאה ישירה של ההגדרה.

   זה כל הנכסים. הקפד לתרגל ליישם אותם! הורידו את דף הצ'יט בתחילת השיעור, הדפיסו אותו - ופתרו את הבעיות.

   לוֹגָרִיתְם. מאפייני הלוגריתם (חיבור וחיסור).

   מאפייני הלוגריתםלעקוב מהגדרתו. וכך הלוגריתם של המספר בעל ידי סיבה אמוגדר כמעריך אליו יש להעלות מספר אכדי לקבל את המספר ב(הלוגריתם קיים רק עבור מספרים חיוביים).

   מניסוח זה עולה כי החישוב x=log a b, שווה ערך לפתרון המשוואה ax=b.לדוגמה, log 2 8 = 3כי 8 = 2 3 . ניסוח הלוגריתם מאפשר להצדיק שאם b=a ג, ואז הלוגריתם של המספר בעל ידי סיבה אשווים עם. ברור גם שנושא הלוגריתם קשור קשר הדוק לנושא העוצמה של מספר.

   עם לוגריתמים, כמו עם כל מספרים, אתה יכול לבצע פעולות חיבור, חיסורולשנות בכל דרך אפשרית. אבל לאור העובדה שהלוגריתמים אינם מספרים רגילים, חלים כאן כללים מיוחדים משלהם, הנקראים מאפיינים בסיסיים.

   חיבור וחיסור של לוגריתמים.

   קח שני לוגריתמים עם אותו בסיס: log xו התחבר א. לאחר מכן הסר אפשר לבצע פעולות חיבור וחיסור:

   כפי שאנו רואים, סכום הלוגריתמיםשווה ללוגריתם של המכפלה, ו הֶבדֵל לוגריתמים- הלוגריתם של המנה. וזה נכון אם המספרים א, איקסו בְּ-חיובי ו a ≠ 1.

   חשוב לציין שההיבט העיקרי בנוסחאות אלו הם אותם בסיסים. אם הבסיסים שונים זה מזה, כללים אלו אינם חלים!

   הכללים לחיבור והפחתה של לוגריתמים עם אותם בסיסים נקראים לא רק משמאל לימין, אלא גם להיפך. כתוצאה מכך, יש לנו את המשפטים ללוגריתם של המכפלה וללוגריתם של המנה.

   לוגריתם של המוצרשני מספרים חיוביים שווה לסכום הלוגריתמים שלהם ; בפרפרזה על המשפט הזה, נקבל את הדברים הבאים, אם המספרים א, איקסו בְּ-חיובי ו a ≠ 1, לאחר מכן:

   לוגריתם של המנהשל שני מספרים חיוביים שווה להפרש בין הלוגריתמים של הדיבידנד והמחלק. במילים אחרות, אם המספרים א, איקסו בְּ-חיובי ו a ≠ 1, לאחר מכן:

   אנו מיישמים את המשפטים לעיל כדי לפתור דוגמאות:

   אם מספרים איקסו בְּ-הם שליליים, אם כך נוסחת לוגריתם המוצרהופך חסר משמעות. אז אסור לכתוב:

   מכיוון שהביטויים log 2 (-8) ו-log 2 (-4) אינם מוגדרים כלל (הפונקציה הלוגריתמית בְּ-= יומן 2 איקסמוגדר רק עבור ערכים חיוביים של הטיעון איקס).

   משפט המוצרישים לא רק עבור שניים, אלא גם עבור מספר בלתי מוגבל של גורמים. זה אומר שלכל טבעי קוכל מספרים חיוביים איקס 1 , איקס 2 , . . . ,x nיש זהות:

   מ משפטי לוגריתם מנהניתן לקבל עוד תכונה אחת של הלוגריתם. ידוע כי יומן א 1=0, לכן,

   אז יש שוויון:

   לוגריתמים של שני מספרים הדדייםעל אותו בסיס יהיו שונים זה מזה רק בסימן. כך:

   לוֹגָרִיתְם. מאפיינים של לוגריתמים

   לוֹגָרִיתְם. מאפיינים של לוגריתמים

   קחו בחשבון שוויון. תן לנו לדעת את הערכים ואנחנו רוצים למצוא את הערך של .

   כלומר, אנחנו מחפשים אקספוננט שאליו אתה צריך להתחנף כדי להגיע .

   תן המשתנה יכול לקבל כל ערך ממשי, ואז ההגבלות הבאות מוטלות על המשתנים: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   אם אנו יודעים את הערכים של ו, ואנו עומדים בפני המשימה למצוא את הלא נודע, אז לשם כך מוצגת פעולה מתמטית, הנקראת לוֹגָרִיתְם.

   כדי למצוא את הערך שאנו לוקחים לוגריתם של מספרעַל קרן :

   הלוגריתם של מספר לבסיס הוא המעריך אליו אתה צריך להעלות כדי לקבל .

   זה זהות לוגריתמית בסיסית:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   הוא בעצם סימון מתמטי הגדרות לוגריתם.

   הלוגריתם של הפעולה המתמטית הוא היפוך של האקספונציה, אז מאפיינים של לוגריתמיםקשורים קשר הדוק למאפייני התואר.

   אנו מפרטים את העיקריות מאפיינים של לוגריתמים:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0 אינץ'/>, 1 אינץ' title=”d1″/>

   4.

   5.

   קבוצת המאפיינים הבאה מאפשרת לך לייצג את המעריך של הביטוי תחת סימן הלוגריתם, או לעמוד בבסיס הלוגריתם כמקדם לפני סימן הלוגריתם:

   6.

   7.

   8.

   9.

   קבוצת הנוסחאות הבאה מאפשרת לך לעבור מלוגריתם עם בסיס נתון ללוגריתם עם בסיס שרירותי, ונקראת נוסחאות מעבר לבסיס חדש:

   10.

   12. (תוצאה מנכס 11)

   

   שלושת המאפיינים הבאים אינם ידועים היטב, אך הם משמשים לעתים קרובות בעת פתרון משוואות לוגריתמיות, או בעת פישוט ביטויים המכילים לוגריתמים:

   13.

   14.

   15.

   מקרים מיוחדים:

   — לוגריתם עשרוני

   — לוגריתם טבעי

   בעת פישוט ביטויים המכילים לוגריתמים, מיושמת גישה כללית:

   1. אנו מייצגים שברים עשרוניים בצורה של שברים רגילים.

   2. אנו מייצגים מספרים מעורבים כשברים לא תקינים.

   3. המספרים בבסיס הלוגריתם ותחת סימן הלוגריתם מפורקים לגורמים ראשוניים.

   4. אנחנו מנסים להביא את כל הלוגריתמים לאותו בסיס.

   5. החל את המאפיינים של לוגריתמים.

   בואו נסתכל על דוגמאות לפישוט ביטויים המכילים לוגריתמים.

   דוגמה 1

   לחשב:

   בואו נפשט את כל המעריכים: המשימה שלנו היא להביא אותם ללוגריתמים, שבסיסם זהה למספר הבסיס של המעריך.

   ==(לפי תכונה 7)=(לפי תכונה 6) =

   החלף את האינדיקטורים שהשגנו בביטוי המקורי. אנחנו מקבלים:

   תשובה: 5.25

   דוגמה 2 חשב:

   

   אנו מביאים את כל הלוגריתמים לבסיס 6 (במקרה זה, הלוגריתמים מהמכנה של השבר "יגרו" למונה):

   בואו נפרק את המספרים מתחת לסימן הלוגריתם לגורמים ראשוניים:

   החל את המאפיינים 4 ו-6:

   אנו מציגים את התחליף

   אנחנו מקבלים:

   תשובה 1

   לוֹגָרִיתְם . זהות לוגריתמית בסיסית.

   מאפיינים של לוגריתמים. לוגריתם עשרוני. לוגריתם טבעי.

   לוֹגָרִיתְם מספר חיובי N בבסיס (ב > 0, ב 1) נקרא המעריך x שאליו צריך להעלות את b כדי לקבל N .

   ערך זה שווה ערך לדברים הבאים: b x = N .

   דוגמאות: log 3 81 = 4 מאז 3 4 = 81 ;

   log 1/3 27 = – 3 כי (1/3) - 3 = 3 3 = 27 .

   ניתן לכתוב את ההגדרה לעיל של הלוגריתם זהות:

   

   מאפיינים בסיסיים של לוגריתמים.

   2) log 1 = 0 כי ב 0 = 1 .

   3) הלוגריתם של המכפלה שווה לסכום הלוגריתמים של הגורמים:

   4) הלוגריתם של המנה שווה להפרש בין הלוגריתמים של הדיבידנד והמחלק:

   5) הלוגריתם של התואר שווה למכפלת המעריך והלוגריתם של הבסיס שלו:

   התוצאה של נכס זה היא כדלקמן: שורש יומן שווה ללוגריתם של מספר השורש חלקי בחזקת השורש:

   

   6) אם הבסיס של הלוגריתם הוא מעלה, אז הערך ניתן להוציא את ההדדיות של המעריך מהסימן של יומן החריזה:

   

   ניתן לשלב את שני הנכסים האחרונים לאחד:

   

   7) הנוסחה של מודול המעבר (כלומר המעבר מבסיס אחד של הלוגריתם לבסיס אחר):

   

   במקרה מסוים, מתי N = איש לנו:

   

   לוגריתם עשרוני שקוראים לו לוגריתם בסיס 10. הוא מסומן lg, כלומר. יומן 10 נ= יומן נ. לוגריתמים של מספרים 10, 100, 1000, . p הם 1, 2, 3, …, בהתאמה, כלומר. יש כל כך הרבה חיוביים

   יחידות, כמה אפסים יש במספר הלוגריתם אחרי אחד. לוגריתמים של מספרים 0.1, 0.01, 0.001, . p הם -1, -2, -3, ..., בהתאמה, כלומר. יש כמה שליליים כמו שיש אפסים במספר הלוגריתם לפני האחד (כולל מספרים שלמים אפס). ללוגריתמים של המספרים הנותרים יש חלק שבר הנקרא מַנטִיסָה. החלק השלם של הלוגריתם נקרא מאפיין. עבור יישומים מעשיים, לוגריתמים עשרוניים הם הנוחים ביותר.

   לוגריתם טבעי שקוראים לו לוגריתם בסיס ה. זה מסומן על ידי ln, כלומר. עֵץ ה נ=ln נ. מספר ההוא לא רציונלי, הערך המשוער שלו הוא 2.718281828. זהו הגבול שאליו המספר (1 + 1 / נ) נעם עלייה בלתי מוגבלת נ(ס"מ. הגבול הנפלא הראשוןבדף מגבלות רצף מספרים).
   ככל שזה נראה מוזר, לוגריתמים טבעיים התבררו כנוחים מאוד בעת ביצוע פעולות שונות הקשורות לניתוח פונקציות. חישוב לוגריתמי בסיס ההרבה יותר מהר מכל בסיס אחר.

• מה צריך היום כדי לאמץ ילד ברוסיה? אימוץ ברוסיה, בנוסף להחלטה אישית אחראית, כרוך במספר הליכים לאימות מדינה של מועמדים. בחירה נוקשה בשלב ההכנה תורמת ליותר […]
• מידע ללא תשלום על ידי TIN או OGRN ממרשם המס ברחבי רוסיה - מקוון בפורטל המאוחד של שירותי מס, מידע על רישום המדינה של ישויות משפטיות, יזמים בודדים, […]
• ענישה על נהיגה ללא מסמכים (רישיון נהיגה, ביטוח, STS) לעיתים, מפאת שכחה, ​​נהגים עולים על ההגה ללא רישיון ומקבלים קנס על נהיגה ללא מסמכים. נזכיר שנהג שנוהג איתו ללא תקלות […]
• פרחים לגברים. איזה סוג של פרחים אתה יכול לתת לגבר? אילו פרחים ניתן לתת לגבר? אין כל כך הרבה פרחים "זכריים", אבל יש כאלה שניתנים לגברים. רשימה קטנה של פרחים לפניכם: חרציות. ורדים. ציפורנים. […]
• תזכיר הוא צורה מיוחדת של מסמך המשמש בסביבה הפנימית של ארגון ומשמש לפתרון מהיר של בעיות ייצור נוכחיות. בדרך כלל מסמך זה נערך במטרה ליצור כמה […]
• מתי וכיצד לקבל את החלק הממומן של הפנסיה בסברבנק? Sberbank הוא בנק שותף של קרן הפנסיה הממלכתית. על בסיס זה, אזרחים שהוציאו פנסיה ממומנת יוכלו להעביר את הממומן […]
• קצבאות ילדים באוליאנובסק ובאזור אוליאנובסק בשנת 2018 בנוסף, בכל האזורים פועלות תוכניות שאושרו בחוק הפדרלי. בואו נראה על מי ועל אילו הטבות אפשר לסמוך. כמו רשויות אזוריות […]
• מדריך מפורט כיצד לערוך ייפוי כוח לייצוג אינטרסים של יחיד בבית המשפט בתביעה אזרחית או בוררות, בתיק מנהלי או פלילי, ניתן לייצג את האינטרסים של התובע וגם של הנתבע על ידי עורך דין: […]

נגזר מהגדרתו. וכך הלוגריתם של המספר בעל ידי סיבה אמוגדר כמעריך אליו יש להעלות מספר אכדי לקבל את המספר ב(הלוגריתם קיים רק עבור מספרים חיוביים).

מניסוח זה עולה כי החישוב x=log a b, שווה ערך לפתרון המשוואה ax=b.לדוגמה, log 2 8 = 3כי 8 = 2 3 . ניסוח הלוגריתם מאפשר להצדיק שאם b=a ג, ואז הלוגריתם של המספר בעל ידי סיבה אשווים עם. ברור גם שנושא הלוגריתם קשור קשר הדוק לנושא העוצמה של מספר.

עם לוגריתמים, כמו עם כל מספרים, אתה יכול לבצע פעולות של חיבור, חיסורולשנות בכל דרך אפשרית. אבל לאור העובדה שהלוגריתמים אינם מספרים רגילים, חלים כאן כללים מיוחדים משלהם, הנקראים מאפיינים בסיסיים.

חיבור וחיסור של לוגריתמים.

קח שני לוגריתמים עם אותו בסיס: log xו התחבר א. לאחר מכן הסר אפשר לבצע פעולות חיבור וחיסור:

log a x+ log a y= log a (x y);

log a x - log a y = log a (x:y).

יומן א(איקס 1 . איקס 2 . איקס 3 ... x k) = log x 1 + log x 2 + log x 3 + ... + log a x k.

מ משפטי לוגריתם מנהניתן לקבל עוד תכונה אחת של הלוגריתם. ידוע כי יומן א 1=0, לכן,

עֵץ א 1 /ב= יומן א 1 - יומן א ב= -לוג א ב.

אז יש שוויון:

log a 1 / b = - log a b.

לוגריתמים של שני מספרים הדדייםעל אותו בסיס יהיו שונים זה מזה רק בסימן. כך:

יומן 3 9= - יומן 3 1 / 9 ; log 5 1 / 125 = -log 5 125.

274. הערות.

א)אם הביטוי שיש להעריך מכיל סְכוּםאוֹ הֶבדֵלמספרים, אז יש למצוא אותם ללא עזרה של טבלאות על ידי חיבור או חיסור רגילים. לדוגמה:

log (35 + 7.24) 5 = 5 log (35 + 7.24) = 5 log 42.24.

ב)בידיעה כיצד ללוגריתם ביטויים, אנו יכולים, הפוך, מהתוצאה הנתונה של הלוגריתם, למצוא את הביטוי שממנו התקבלה תוצאה זו; אז אם

עֵץ איקס= יומן א+ יומן ב- 3 יומנים עם,

קל לדמיין את זה

ב)לפני שנמשיך לשקול את המבנה של טבלאות לוגריתמיות, נציין כמה מאפיינים של לוגריתמים עשרוניים, כלומר. אלה שבהם המספר 10 נלקח כבסיס (רק לוגריתמים כאלה משמשים לחישובים).

פרק שני.

מאפיינים של לוגריתמים עשרוניים.

275 . א) מאז 10 1 = 10, 10 2 = 100, 10 3 = 1000, 10 4 = 10000, וכו ', אז log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4 וכו'.

אומר, הלוגריתם של מספר שלם המיוצג על ידי אחד עם אפסים הוא מספר שלם חיובי המכיל כמה וכמה אפסים בתמונה של המספר.

בדרך זו: log 100,000 = 5, עֵץ 1000 000 = 6 , וכו.

ב) כי

log 0.1 = -l; log 0.01 = - 2; log 0.001 == -3; log 0.0001 = - 4,וכו '

אומר, הלוגריתם של שבר עשרוני המיוצג על ידי יחידה עם אפסים מובילים הוא מספר שלם שלילי המכיל כמה יחידות שליליות כמו שיש אפסים בתמונת השבר, כולל 0 מספרים שלמים.

בדרך זו: log 0.00001= - 5, log 0.000001 = -6,וכו '

ב)קחו למשל מספר שלם שאינו מיוצג על ידי יחידה עם אפסים. 35, או מספר שלם עם שבר, למשל. 10.7. הלוגריתם של מספר כזה אינו יכול להיות מספר שלם, שכן בהעלאת 10 לחזקה בעלת מעריך שלם (חיובי או שלילי), נקבל 1 עם אפסים (אחרי או לפני 1). נניח כעת שהלוגריתם של מספר כזה הוא שבר כלשהו א / ב . אז יהיה לנו שוויון

אבל השוויון הזה בלתי אפשרי, כמו 10א הוא 1 עם אפסים, בעוד חזקה 35ב ו 10,7ב אין אינדיקטור ב לא יכול לתת 1 עם אפסים. לפיכך, לא ניתן לאפשר זאת יומן 35ו יומן 10.7היו שווים לשברים. אבל מהמאפיינים של הפונקציה הלוגריתמית, אנו יודעים () שלכל מספר חיובי יש לוגריתם; לפיכך, לכל אחד מהמספרים 35 ו-10.7 יש לוגריתם משלו, ומכיוון שהוא אינו יכול להיות מספר שלם או שבריר, זהו מספר אי-רציונלי, ולכן לא ניתן לבטא אותו במדויק באמצעות מספרים. בדרך כלל, לוגריתמים אי-רציונליים מתבטאים בערך כשבר עשרוני עם מספר מקומות עשרוניים. המספר השלם של השבר הזה (למרות שהוא היה "0 שלמים") נקרא מאפיין, והחלק השברי הוא המנטיסה של הלוגריתם. אם, למשל, הלוגריתם הוא 1,5441 , אז המאפיין שלו הוא 1 , והמנטיסה היא 0,5441 .

ז)ניקח לדוגמא מספר שלם או מעורב. 623 אוֹ 623,57 . הלוגריתם של מספר כזה מורכב ממאפיין ומנטיסה. מסתבר שללוגריתמים עשרוניים יש את הנוחות ש אנחנו תמיד יכולים למצוא את המאפיין שלהם לפי סוג אחד של מספר . לשם כך, אנו סופרים כמה ספרות יש במספר שלם נתון, או בחלק השלם של מספר מעורב. בדוגמאות שלנו למספרים אלה 3 . לכן, כל אחד מהמספרים 623 ו 623,57 יותר מ-100 אך פחות מ-1000; מה שאומר שהלוגריתם של כל אחד מהם גדול יותר יומן 100, כלומר יותר 2 , אבל פחות log 1000, כלומר פחות 3 (זכור שלמספר גדול יותר יש גם לוגריתם גדול יותר). כתוצאה מכך, log 623 = 2,..., ו log 623.57 = 2,... (נקודות מחליפות מנטיסות לא ידועות).

כך אנו מוצאים:

10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,...

1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,...

תנו באופן כללי למספר שלם נתון, או לחלק שלם של מספר מעורב נתון, להכיל M ספרות. מאז המספר השלם הקטן ביותר המכיל M ספרות, שם 1 עם M - 1 אפסים נגררים, אם כן (מציין את המספר הנתון נ) נוכל לכתוב את אי השוויון:

ולכן

M - 1 < log N < M ,

log N = ( M- 1) + שבר חיובי.

אז המאפיין logN = M - 1 .

אנחנו רואים כך את זה המאפיין של הלוגריתם של מספר שלם או מעורב מכיל כמה חיוביים כמו שיש ספרות בחלק השלם של המספר ללא אחד.

עם זאת בחשבון, אנו יכולים לכתוב ישירות:

log 7,205 = 0,...; log83 = 1,...; log 720.4 = 2,...וכו '

ה)בואו ניקח כמה שברים עשרוניים קטנים מ 1 (כלומר שיש 0 מספרים שלמים): 0,35; 0,07; 0,0056; 0,0008, וכו '

לפיכך, כל אחד מהלוגריתמים הללו מוקף בין שני מספרים שלמים שליליים הנבדלים באחד; כך שכל אחד מהם שווה למספר הקטן מבין המספרים השליליים הללו המוגדל בשבר חיובי כלשהו. לדוגמה, log0.0056= -3 + שבר חיובי. נניח שהשבר הזה הוא 0.7482. ואז, זה אומר:

log 0.0056 = - 3 + 0.7482 (= - 2.2518).

סכומים כגון - 3 + 0,7482 , המורכב ממספר שלם שלילי ושבר עשרוני חיובי, הסכים לכתוב מקוצר בחישובים לוגריתמיים באופן הבא: 3 ,7482 (מספר כזה אומר: 3 עם מינוס, 7482 עשרת אלפים.), כלומר שמים סימן מינוס מעל המאפיין כדי להראות שהוא מתייחס רק למאפיין הזה, ולא למנטיסה, שנותרה חיובית. לפיכך, מהטבלה לעיל, ניתן לראות זאת

log 0.35 == 1 ,....; log 0.07 = 2 ,....; log 0.0008 = 4 ,....

תן בכלל . יש שבר עשרוני שבו הספרה המשמעותית הראשונה α עלויות M אפסים, כולל 0 מספרים שלמים. אז ברור ש

- M < log A < - (M- 1).

מאז מתוך שני מספרים שלמים:- M ו - (M- 1) יש פחות M , לאחר מכן

log A = - M+ שבר חיובי,

ולכן המאפיין log A = - M (עם מנטיס חיובי).

בדרך זו, המאפיין של הלוגריתם של שבר עשרוני קטן מ-1 מכיל שליליים כמו שיש אפסים בתמונה של השבר העשרוני מול הספרה המשמעותית הראשונה, כולל מספרים שלמים אפס; המנטיסה של לוגריתם כזה היא חיובית.

ה)תכפילו מספר כלשהו נ(שלם או חלקי - זה לא משנה) ב-10, ב-100 ב-1000..., בדרך כלל ב-1 עם אפסים. בוא נראה איך זה משתנה log N. מכיוון שהלוגריתם של המכפלה שווה לסכום הלוגריתמים של הגורמים, אז

log(N 10) = log N + log 10 = log N + 1;

log(N 100) = log N + log 100 = log N + 2;

log(N 1000) = log N + log 1000 = log N + 3;וכו '

מתי ל log Nנוסיף איזה מספר שלם, אז תמיד נוכל להוסיף את המספר הזה למאפיין, ולא למנטיסה.

אז, אם log N = 2.7804, אז 2.7804 + 1 = 3.7804; 2.7804 + 2 = 4.7801 וכו';

או אם log N = 3.5649, אז 3.5649 + 1 = 2.5649; 3.5649 + 2 = 1.5649 וכו'.

מכפלת מספר ב-10, 100, 1000, .., בדרך כלל ב-1 עם אפסים, המנטיסה של הלוגריתם לא משתנה, והמאפיין גדל ביחידות רבות ככל שיש אפסים במכפיל .

באופן דומה, אם לוקחים בחשבון שהלוגריתם של המנה שווה ללוגריתם של הדיבידנד ללא הלוגריתם של המחלק, אנו מקבלים:

log N / 10 = log N - log 10 = log N -1;

log N / 100 = log N - log 100 = log N -2;

log N / 1000 = log N - log 1000 = log N -3;וכו '

אם נסכים, בעת הפחתת מספר שלם מהלוגריתם, להחסיר את המספר השלם הזה תמיד מהמאפיין, ולהשאיר את המנטיסה ללא שינוי, אז נוכל לומר:

מחלוקת מספר ב-1 עם אפסים, המנטיסה של הלוגריתם לא משתנה, והמאפיין יורד ביחידות רבות כמו שיש אפסים במחלק.

276. השלכות.מרכוש ( ה) נוכל להסיק את שתי ההשלכות הבאות:

א) המנטיסה של הלוגריתם של מספר עשרוני לא משתנה מהזזת המספר על ידי פסיק , כי הזזת פסיק שווה ערך להכפלה או לחלוקה ב-10, 100, 1000 וכו'. לפיכך, הלוגריתמים של מספרים:

0,00423, 0,0423, 4,23, 423

נבדלים רק במאפיינים, אך לא במנטיסות (בתנאי שכל המנטיסות חיוביות).

ב) המנטיסה של מספרים שיש להם אותו חלק משמעותי, אבל נבדלות רק באפסים בסוף, זהות: אז, הלוגריתמים של מספרים: 23, 230, 2300, 23,000 שונים רק במאפיינים.

תגובה. ממאפיינים אלו של לוגריתמים עשרוניים, ניתן לראות כי אנו יכולים למצוא את המאפיין של הלוגריתם של מספר שלם ושבר עשרוני ללא עזרת טבלאות (זו הנוחות הגדולה של לוגריתמים עשרוניים); כתוצאה מכך, רק מנטיסה אחת ממוקמת בטבלאות לוגריתמיות; בנוסף, מכיוון שמציאת הלוגריתמים של השברים מצטמצמת למציאת הלוגריתמים של המספרים השלמים (הלוגריתם של השבר \u003d הלוגריתם של המונה ללא הלוגריתם של המכנה), המנטיסה של הלוגריתמים של מספרים שלמים בלבד ממוקמות ב- שולחנות.

פרק שלישי.

המכשיר והשימוש בטבלאות ארבע ספרות.

277. מערכות לוגריתמים.מערכת לוגריתמים היא קבוצה של לוגריתמים המחושבים עבור סדרה של מספרים שלמים עוקבים באותו בסיס. נעשה שימוש בשתי מערכות: מערכת הלוגריתמים הרגילים או העשרוניים, שבה המספר נלקח כבסיס 10 , והמערכת של מה שנקרא לוגריתמים טבעיים, שבה לוקחים את המספר האי-רציונלי כבסיס (מסיבות מסוימות המובנות בענפים אחרים של מתמטיקה) 2,7182818 ... לחישובים משתמשים בלוגריתמים עשרוניים, בשל הנוחות שציינו כשמנינו את המאפיינים של לוגריתמים כאלה.

לוגריתמים טבעיים נקראים גם הלוגריתמים של נאפייר על שם ממציא הלוגריתמים, מתמטיקאי סקוטי. נפרה(1550-1617), ולוגריתמים עשרוניים - מאת בריג על שם פרופסור בריגה(בן זמנו וידידו של נאפייר), שהרכיב לראשונה טבלאות של לוגריתמים אלו.

278. טרנספורמציה של לוגריתם שלילי ללוגריתם עם מנטיס חיובי, והתמרה הפוכה. ראינו שהלוגריתמים של מספרים פחות מ-1 הם שליליים. לפיכך, הם מורכבים ממאפיין שלילי ומנטיסה שלילית. לוגריתמים כאלה תמיד יכולים לעבור טרנספורמציה כך שהמנטיסה שלהם תהיה חיובית, והמאפיין יישאר שלילי. כדי לעשות זאת, מספיק להוסיף יחידה חיובית למנטיסה, ויחידה שלילית למאפיין (שממנה, כמובן, ערך הלוגריתם לא ישתנה).

אם, למשל, יש לנו את הלוגריתם - 2,0873 , אז אתה יכול לכתוב:

- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,

או בקיצור:

לעומת זאת, כל לוגריתם בעל מאפיין שלילי ומנטיסה חיובית יכול להפוך לשלילי. כדי לעשות זאת, זה מספיק כדי לצרף יחידה שלילית למנטיסה חיובית, ואחת חיובית למאפיין שלילי: אז אתה יכול לכתוב:

279. תיאור טבלאות ארבע ספרות.לפתרון רוב הבעיות המעשיות, טבלאות ארבע ספרות מספיקות למדי, שהטיפול בהן פשוט מאוד. טבלאות אלו (עם ה"לוגריתמים" שלהן בראש) ממוקמות בסוף ספר זה, וחלק קטן מהן (כדי להסביר את המיקום) מודפס בעמוד זה. הן מכילות גמל שלמה.

לוגריתמים.

לוגריתמים של כל המספרים השלמים מ 1 לפני 9999 כולל, מחושב לארבעה מקומות עשרוניים, האחרון מבין המקומות העשרוניים הללו מוגדל ב- 1 בכל המקרים שבהם המקום ה-5 העשרוני יצטרך להיות 5 או יותר מ-5; לכן, טבלאות בנות 4 ספרות נותנות למנטיסות משוערות עד 1 / 2 חלק עשרת אלפים (עם חסר או עם עודף).

מכיוון שאנו יכולים לאפיין ישירות את הלוגריתם של מספר שלם או שבר עשרוני, בהתבסס על המאפיינים של לוגריתמים עשרוניים, עלינו לקחת רק את המנטיסה מהטבלאות; יחד עם זאת, יש לזכור שמיקום הפסיק במספר עשרוני, כמו גם מספר האפסים בסוף המספר, אינם משפיעים על ערך המנטיסה. לכן, כשמוצאים את המנטיסה למספר נתון, אנו פוסלים את הפסיק במספר זה, כמו גם את האפסים בסוף שלו, אם יש, ומוצאים את המנטיסה של המספר השלם שנוצר לאחר מכן. במקרה זה, עשויים להופיע המקרים הבאים.

1) מספר שלם מורכב מ-3 ספרות.לדוגמה, בואו נמצא את המנטיסה של הלוגריתם של המספר 536. שתי הספרות הראשונות של מספר זה, כלומר 53, נמצאות בטבלאות בעמודה האנכית הראשונה משמאל (ראה טבלה). לאחר שמצאנו את המספר 53, אנו נעים ממנו לאורך הקו האופקי ימינה עד שהקו הזה מצטלב עם עמודה אנכית העוברת דרך אחד המספרים 0, 1, 2, 3, ... 9, המוגדרים למעלה (ו למטה) של הטבלה, המייצגת את הספרה ה-3 של המספר הזה, כלומר בדוגמה שלנו, המספר 6. בצומת נקבל את המנטיסה 7292 (כלומר 0.7292), השייכת ללוגריתם של המספר 536. באופן דומה, עבור המספר 508 נמצא את המנטיסה 0.7059, עבור המספר 500 נמצא 0.6990 וכו'.

2) מספר שלם מורכב מ-2 או 1 ספרה.לאחר מכן אנו מקצים נפשית אפס אחד או שניים למספר זה ומוצאים את המנטיסה עבור המספר התלת ספרתי שנוצר כך. לדוגמה, אנו מקצים אפס אחד למספר 51, ממנו נקבל 510 ונמצא את המנטיסה 7070; אנו מקצים 2 אפסים למספר 5 ומוצאים את המנטיסה 6990 וכו'.

3) מספר שלם מבוטא עם 4 ספרות.לדוגמה, אתה צריך למצוא את המנטיסה של יומן 5436. אז תחילה אנו מוצאים בטבלאות, כפי שצוין זה עתה, את המנטיסה עבור המספר המתואר על ידי 3 הספרות הראשונות של מספר זה, כלומר עבור 543 (מנטיסה זו תהיה 7348 ); לאחר מכן אנו עוברים מהמנטיסה שנמצאה לאורך הקו האופקי ימינה (לצד ימין של הטבלה, הממוקם מאחורי הקו האנכי העבה) עד להצטלבות עם העמודה האנכית העוברת דרך אחד המספרים: 1, 2 3, . .. 9, עומד בחלק העליון (ובתחתית) של חלק זה של הטבלה, המייצג את הספרה הרביעית של מספר נתון, כלומר, בדוגמה שלנו, המספר 6. בצומת נמצא את התיקון (מספר 5), שיש ליישם במוח על המנטיסה 7348 כדי לקבל את המנטיסה של המספר 5436; כך נקבל מנטיס של 0.7353.

4) מספר שלם מבוטא עם 5 ספרות או יותר.לאחר מכן נזרוק את כל הספרות, מלבד ה-4 הראשונות, וניקח מספר בן ארבע ספרות משוער, ונגדיל את הספרה האחרונה של המספר הזה ב-1. במקרה שבו הספרה החמישית שנמחקה של המספר היא 5 או יותר מ-5. לכן, במקום 57842 ניקח 5784, במקום 30257 ניקח 3026, במקום 583263 ניקח 5833 וכו'. עבור מספר ארבע ספרות מעוגל זה, אנו מוצאים את המנטיסה כפי שהוסברה כעת.

בהנחיית הוראות אלה, נמצא, למשל, את הלוגריתמים של המספרים הבאים:

36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.

קודם כל, בלי להתייחס לטבלאות לעת עתה, נניח כמה מאפיינים, ונשאיר מקום למנטיסות, שאותן נכתוב אחרי:

log 36.5 = 1,.... log 0.00345 = 3 ,....

log 804.7 = 2,.... log 7.2634 = 0,....

log 0.26 = 1 ,.... log 3456.86 = 3,....

log 36.5 = 1.5623; log 0.00345 = 3.5378;

log 804.7 = 2.9057; log 7.2634 = 0.8611;

log 0.26 = 1.4150; log 3456.86 = 3.5387.

280. הערה. בחלק מהטבלאות בעלות ארבע ספרות (לדוגמה, בטבלאות V. Lorchenko and N. Ogloblin, S. Glazenap, N. Kamenshchikova) תיקונים עבור הספרה הרביעית של מספר זה אינם ממוקמים. כאשר עוסקים בטבלאות כאלה, יש למצוא את התיקונים הללו באמצעות חישוב פשוט, שניתן לבצע על בסיס האמת הבאה: אם המספרים גדולים מ-100, וההפרשים ביניהם קטנים מ-1, אז ללא רגישות טעות ניתן להניח כי ההבדלים בין הלוגריתמים הם פרופורציונליים להבדלים בין המספרים המתאימים . בואו, למשל, עלינו למצוא את המנטיסה המתאימה למספר 5367. המנטיסה הזו, כמובן, זהה למספר 536.7. אנו מוצאים את המנטיסה 7292 בטבלאות של המספר 536. משווים את המנטיסה הזו עם המנטיסה 7300 הסמוכה מימין, המקבילה למספר 537, נבחין שאם המספר 536 יגדל ב-1, אז המנטיסה שלו תגדל ב-8 עשר אלפיות (8 זה מה שנקרא הבדל טבלאיבין שתי מנטיסות סמוכות); אם המספר 536 יגדל ב-0.7, המנטיסה שלו תגדל לא ב-8 עשרת אלפים, אלא במספר קטן יותר. איקס עשרת אלפים, שעל פי המידתיות המותרת, לעמוד בשיעור:

איקס :8=0.7:1; איפה איקס = 8 07 = 5,6,

אשר מעוגל ל-6 עשרת אלפים. המשמעות היא שהמנטיסה עבור המספר 536.7 (ולכן עבור המספר 5367) תהיה: 7292 + 6 = 7298.

שימו לב שמציאת מספר ביניים לפי שני מספרים סמוכים בטבלאות נקראת שִׁרבּוּב.האינטרפולציה המתוארת כאן נקראת יַחֲסִי, שכן הוא מבוסס על ההנחה שהשינוי בלוגריתם הוא פרופורציונלי לשינוי במספר. זה נקרא גם ליניארי, מכיוון שהוא מניח שמבחינה גרפית השינוי בפונקציה הלוגריתמית מתבטא על ידי קו ישר.

281. גבול השגיאה של הלוגריתם המשוער.אם המספר שמחפשים את הלוגריתם שלו הוא מספר מדויק, אז עבור מגבלת השגיאה של הלוגריתם שלו שנמצאת בטבלאות בנות 4 ספרות, אנחנו יכולים, כפי שאמרנו, לקחת 1 / 2 חלק עשרת אלפים. אם המספר הנתון אינו מדויק, אז למרווח הטעות הזה, יש להוסיף גם את הגבול של טעות נוספת הנובעת מאי דיוק המספר עצמו. הוכח (אנחנו משמיטים את ההוכחה הזו) שעבור מגבלה כזו אפשר לקחת את המוצר

א(ד +1) עשרת אלפים.,

שבו א הוא מרווח הטעות של המספר הכי לא מדויק, בהנחה ש 3 ספרות נלקחות בחלק השלם שלו, א ד הבדל טבלאי של המנטיסה המקביל לשני מספרים תלת ספרתיים עוקבים שביניהם המספר הלא מדויק הזה מוקף. לפיכך, הגבול של השגיאה הסופית של הלוגריתם יבוא לידי ביטוי בנוסחה:

1 / 2 + א(ד +1) העשרת אלפים

דוגמא. מצא יומן π , לוקח עבור π מספר משוער 3.14, מדויק ל 1 / 2 מֵאְית.

על ידי הזזת הפסיק אחרי הספרה ה-3 במספר 3.14, ספירה משמאל, נקבל את המספר התלת ספרתי 314, בדיוק עד 1 / 2 יחידות; זה אומר ששולי הטעות של מספר לא מדויק, כלומר, מה שציינו באות א , אם 1 / 2 מהטבלאות אנו מוצאים:

log 3.14 = 0.4969.

הבדל טבלאי ד בין המנטיסים של המספרים 314 ו-315 הוא 14, כך שהשגיאה של הלוגריתם שנמצא תהיה פחותה

1 / 2 + 1 / 2 (14 +1) = 8 עשרת אלפים.

מכיוון שאיננו יודעים על הלוגריתם של 0.4969 אם הוא מתחת או מעל, אנו יכולים רק להבטיח שהלוגריתם המדויק π הוא בין 0.4969 - 0.0008 ל-0.4969 + 0.0008, כלומר 0.4961< log π < 0,4977.

282. מצא מספר מלוגריתם נתון. כדי למצוא מספר לפי לוגריתם נתון, ניתן להשתמש באותן טבלאות, לפיהן נמצאות המנטיסה של המספרים הללו; אבל יותר נוח להשתמש בטבלאות אחרות שבהן ממוקמים מה שנקרא אנטילוגריתמים, כלומר, מספרים התואמים למנטיסות נתונות. טבלאות אלו, המסומנות "אנטילוגריתמים" בחלק העליון, ממוקמות בסוף ספר זה, בעקבות טבלאות הלוגריתמים; חלק קטן מהן ממוקם בדף זה (להסבר).

תנו למנטיסה 2863 בת 4 ספרות (אנחנו לא שמים לב למאפיין) והיא נדרשת למצוא את המספר השלם המתאים. לאחר מכן, עם טבלאות של אנטילוגריתמים, עלינו להשתמש בהן בדיוק באותו אופן כפי שהוסבר קודם למציאת המנטיסה עבור מספר נתון, כלומר: נמצא את 2 הספרות הראשונות של המנטיסה בעמודה השמאלית הראשונה. לאחר מכן נעבור מהמספרים הללו לאורך הקו האופקי ימינה עד להצטלבות עם העמודה האנכית שמגיעה מהספרה ה-3 של המנטיסה, אותה יש לחפש בשורה העליונה (או התחתונה). בצומת אנו מוצאים את המספר בן ארבע הספרות 1932, המקביל למנטיסה 286. לאחר מכן ממספר זה אנו מתקדמים לאורך הקו האופקי ימינה עד להצטלבות עם העמודה האנכית המגיעה מהספרה ה-4 של המנטיסה, אשר חייבת נמצא בחלק העליון (או התחתון) בין המספרים 1, 2 לשים שם , 3,... 9. בצומת, אנו מוצאים את התיקון 1, אותו יש ליישם (במוח) למספר 1032 שנמצא קודם לכן על מנת לקבל את המספר המתאים למנטיסה של 2863.

לפיכך, המספר יהיה 1933. לאחר מכן, תוך שימת לב למאפיין, יש צורך לשים את הכבוש במקום המתאים במספר 1933. לדוגמה:

אם עֵץ איקס = 3.2863, אם כן איקס = 1933,

„ עֵץ x= 1,2863, „ איקס = 19,33,

, עֵץ איקס = 0,2&63, „ איקס = 1,933,

„ עֵץ איקס = 2 ,2863, „ איקס = 0,01933

הנה עוד דוגמאות:

עֵץ איקס = 0,2287, איקס = 1,693,

עֵץ איקס = 1 ,7635, איקס = 0,5801,

עֵץ איקס = 3,5029, איקס = 3184,

עֵץ איקס = 2 ,0436, איקס = 0,01106.

אם המנטיסה מכילה 5 ספרות או יותר, אז ניקח רק את 4 הספרות הראשונות, נזרוק את השאר (ומגדיל את הספרה הרביעית ב-1 אם הספרה החמישית היא חמש או יותר). לדוגמה, במקום מנטיסה 35478 ניקח 3548, במקום 47562 ניקח 4756.

283. הערה.את התיקון לספרות הרביעית והאחרות של המנטיסה ניתן למצוא גם על ידי אינטרפולציה. לכן, אם המנטיסה היא 84357, אז, לאחר שמצאנו את המספר 6966 המתאים למנטיסה 843, נוכל לנמק כך: אם המנטיסה גדלה ב-1 (אלף), כלומר 844 נעשה, אז המספר, כפי שניתן לעשות. נראה מהטבלאות, יגדל ב-16 יחידות; אם המנטיסה גדלה לא ב-1 (אלף), אלא ב-0.57 (אלף), אז המספר יגדל ב- איקס יחידות, ו איקס צריך לענות על הפרופורציות:

איקס : 16 = 0.57: 1, מאיפה x = 16 0,57 = 9,12.

המשמעות היא שהמספר הרצוי יהיה 6966 + 9.12 = 6975.12 או (מוגבל לארבע ספרות בלבד) 6975.

284. מגבלת השגיאה של המספר שנמצא.מוכח שבמקרה שבו במספר שנמצא הפסיק הוא אחרי הספרה ה-3 משמאל, כלומר כאשר המאפיין של הלוגריתם הוא 2, ניתן לקחת את הסכום כשולי הטעות

איפה א הוא מרווח הטעות של הלוגריתם (מבוטא בעשרת אלפים) שבאמצעותו נמצא המספר, וכן ד - ההפרש בין המנטיסים של שני מספרים תלת ספרתיים עוקבים שביניהם מוקף המספר שנמצא (עם פסיק אחרי הספרה ה-3 משמאל). כאשר המאפיין אינו 2, אלא אחר, אז במספר המצוי יהיה צורך להזיז את הפסיק שמאלה או ימינה, כלומר לחלק או להכפיל את המספר בחזק מסוים של 10. במקרה זה, השגיאה של התוצאה תחולק או תכופל באותה חזקה של 10.

הבה, למשל, נמצא מספר לפי הלוגריתם 1,5950 , שידוע כמדויק עד 3 עשרת אלפים; ואז א = 3 . המספר המתאים ללוגריתם זה, שנמצא מטבלת האנטי-לוגריתמים, הוא 39,36 . אם תזיז את הפסיק אחרי הספרה השלישית משמאל, יהיה לנו מספר 393,6 בֵּין 393 ו 394 . מטבלאות הלוגריתמים, אנו רואים שההבדל בין המנטיסים המקבילים לשני המספרים הללו הוא 11 עשרת אלפים; אומר ד = 11 . השגיאה של המספר 393.6 תהיה פחותה

אז שגיאת המספר 39,36 יהיה פחות 0,05 .

285. פעולות על לוגריתמים בעלי מאפיינים שליליים.הוספה והפחתה של לוגריתמים אינם גורמים לקשיים, כפי שניתן לראות מהדוגמאות הבאות:

אין גם קושי להכפיל את הלוגריתם במספר חיובי, למשל:

בדוגמה האחרונה, המנטיסה החיובית מוכפלת בנפרד ב-34, ואז המאפיין השלילי מוכפל ב-34.

אם הלוגריתם של מאפיין שלילי ומנטיסה חיובית מוכפל במספר שלילי, אז הם פועלים בשתי דרכים: או שהלוגריתם שניתן קודם לכן הופך לשלילי, או שהמנטיסה והמאפיין מוכפלים בנפרד והתוצאות משולבות יחד, עבור דוגמא:

3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;

3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.

כאשר מחלקים, ישנם שני מקרים: 1) המאפיין השלילי מחולק ו 2) אינו מתחלק במחלק. במקרה הראשון, המאפיין והמנטיסה מופרדים בנפרד:

10 ,3784: 5 = 2 ,0757.

במקרה השני, כל כך הרבה יחידות שליליות מתווספות למאפיין כך שהמספר המתקבל מתחלק במחלק; אותו מספר של יחידות חיוביות מתווספות למנטיסה:

3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.

הטרנספורמציה הזו חייבת להיעשות במוח, אז הפעולה מסודרת כך:

286. החלפת לוגריתמים מופחתים במונחים.כאשר מחשבים ביטוי מורכב כלשהו באמצעות לוגריתמים, עליך להוסיף כמה לוגריתמים, לגרוע אחרים; במקרה זה, בדרך הרגילה של ביצוע פעולות, הם מוצאים בנפרד את סכום המונחים של הלוגריתמים, ולאחר מכן את סכום החסרים, ומפחיתים את השני מהסכום הראשון. לדוגמה, אם יש לנו:

עֵץ איקס = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,

אז הביצוע הרגיל של הפעולות יהיה ממוקם כך:

עם זאת, אפשר להחליף חיסור בחיבור. כך:

עכשיו אתה יכול לסדר את החישוב כך:

287. דוגמאות לחישובים.

דוגמה 1. הערכת ביטוי:

אם A \u003d 0.8216, B \u003d 0.04826, C \u003d 0.005127ו D = 7.246.

אנו לוגריתמים את הביטוי הזה:

עֵץ איקס= 1/3 לוג A + 4 לוג B - 3 לוג C - 1/3 לוג D

כעת, על מנת למנוע אובדן זמן מיותר ולצמצם את האפשרות לשגיאות, אנו קודם כל מסדרים את כל החישובים מבלי לבצע אותם עדיין ומבלי להתייחס, לפיכך, לטבלאות:

לאחר מכן, אנו לוקחים את הטבלאות ומניחים את הלוגריתמים במקומות הריקים השמאלי:

גבול הטעות.ראשית, בואו נמצא את מגבלת השגיאות של המספר איקס 1 = 194,5 , שווה ל:

אז, קודם כל, אתה צריך למצוא א , כלומר, מרווח הטעות של הלוגריתם המשוער, מבוטא בעשרת אלפים. בואו נניח שהמספרים האלה א ב גו דכולם מדויקים. אז השגיאות בלוגריתמים בודדים יהיו כדלקמן (בעשרת אלפים):

ב logA.......... 1 / 2

ב 1/3 לוג A......... 1 / 6 + 1 / 2 = 2 / 3

( 1 / 2 הוסיף כי כאשר מחלקים ב-3 לוגריתמים של 1.9146, עיגלנו את המנה על ידי השלכת הספרה החמישית שלה, ולכן עשינו שגיאה נוספת, פחות 1 / 2 העשרת אלפים).

כעת אנו מוצאים את מרווח הטעות של הלוגריתם:

א = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (עשרת אלפים).

בוא נגדיר יותר ד . כי איקס 1 = 194,5 , ואז 2 מספרים שלמים רצופים שביניהם הוא איקס 1 רָצוֹן 194 ו 195 . הבדל טבלאי ד בין המנטיסים המקבילים למספרים אלה שווה ל 22 . אז מרווח הטעות של המספר איקס 1 יש:

כי איקס = איקס 1 : 10, ואז מרווח הטעות במספר איקס שווים 0,3:10 = 0,03 . לפיכך, המספר שמצאנו 19,45 שונה מהמספר המדויק בפחות מ 0,03 . מכיוון שאיננו יודעים אם הקירוב שלנו נמצא עם חסר או עם עודף, אנחנו יכולים רק להבטיח כי

19,45 + 0,03 > איקס > 19,45 - 0,03 , כלומר

19,48 > איקס > 19,42 ,

ולפיכך, אם נקבל איקס =19,4 , אז יהיה לנו קירוב עם חסרון עד 0.1.

דוגמה 2לחשב:

איקס = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .

מכיוון שלמספרים שליליים אין לוגריתמים, אנו מוצאים תחילה:

איקס" = (2,31) 3 5 √72

לפי פירוק:

עֵץ איקס"= 3 לוג 2.31 + 1/5 לוג72.

לאחר החישוב יהיה:

איקס" = 28,99 ;

כתוצאה מכך,

איקס = - 28,99 .

דוגמה 3. לחשב:

לא ניתן ליישם כאן לוגריתם רציף, שכן מתחת לסימן השורש עומד עם y m m a. במקרים כאלה, הנוסחה מחושבת בחלקים.

ראשית אנו מוצאים נ = 5 √8 , לאחר נ 1 = 4 √3 ; ואז, על ידי תוספת פשוטה, אנו קובעים נ+ נ 1 , ולבסוף לחשב 3 √נ+ נ 1 ; יתברר:

N = 1.514, נ 1 = 1,316 ; נ+ נ 1 = 2,830 .

עֵץ איקס= יומן 3 √ 2,830 = 1 / 3 יומן 2,830 = 0,1506 ;

איקס = 1,415 .

פרק ארבע.

משוואות אקספוננציאליות ומשוואות לוגריתמיות.

288. משוואה מעריכית היא כזו שבה הלא נודע נכלל במעריך, ו לוגריתמי- אלה שבהם האלמוני נכנס מתחת לשלט עֵץ. ניתן לפתור משוואות כאלה רק במקרים מיוחדים, וצריך להסתמך על תכונות הלוגריתמים ועל העיקרון שאם המספרים שווים, אז הלוגריתמים שלהם שווים, ולהפך, אם הלוגריתמים שווים, אז ההתאמה המקבילה המספרים שווים.

דוגמה 1פתור את המשוואה: 2 איקס = 1024 .

אנו לוגריתמים את שני הצדדים של המשוואה:

דוגמה 2פתור את המשוואה: א 2x - א איקס = 1 . לשים א איקס = בְּ- , נקבל משוואה ריבועית:

y 2 - בְּ- - 1 = 0 ,

כי 1-√5 < 0 , אז המשוואה האחרונה בלתי אפשרית (פונקציה א איקס תמיד יש מספר חיובי), והראשון נותן:

דוגמה 3פתור את המשוואה:

עֵץ( a + x) + יומן ( b + x) = יומן ( c + x) .

אפשר לכתוב את המשוואה כך:

עֵץ[( a + x) (b + x)] = יומן ( c + x) .

משוויון הלוגריתמים אנו מסיקים על שוויון המספרים:

(a + x) (b + x) = c + x .

זוהי משוואה ריבועית, שפתרונה אינו קשה.

פרק חמישי.

ריבית דריבית, תשלומים לתקופות ותרומות דחופות.

289. הבעיה העיקרית של ריבית דריבית.מה כמות ההון א רובל, נתון בצמיחה על ידי ר ריבית דריבית לאחר ט שנים ( ט הוא מספר שלם)?

אומרים שההון ניתן בריבית דריבית אם מביאים בחשבון את מה שמכונה "ריבית על הריבית", כלומר אם כספי הריבית המגיעים על ההון מתווספים בסוף כל שנה להון כדי להגדיל אותו עם ריבית בשנים שלאחר מכן.

כל רובל הון שניתן לו ר %, תוך שנה אחת יביא רווח ע / 100 רובל, וכתוצאה מכך, כל רובל הון בשנה אחת יהפוך ל 1 + ע / 100 רובל (לדוגמה, אם ההון ניתן עבור 5 %, אז כל רובל בשנה יהפוך ל 1 + 5 / 100 , כלומר ב 1,05 רוּבָּל).

מציין לקיצור השבר ע / 100 אות אחת, למשל, ר , אנו יכולים לומר שכל רובל הון בשנה יהפוך ל 1 + ר רובל; כתוצאה מכך, א רובל יהפוך תוך שנה ל א (1 + ר ) לשפשף. שנה לאחר מכן, כלומר, שנתיים לאחר תחילת הצמיחה, כל רובל מהם א (1 + ר ) לשפשף. יחזור ל 1 + ר לשפשף.; המשמעות היא שכל ההון יומר ל א (1 + ר ) 2 לשפשף. באותו אופן אנו מוצאים שאחרי שלוש שנים הבירה תהיה א (1 + ר ) 3 , בעוד ארבע שנים יהיה א (1 + ר ) 4 ,... באופן כללי דרך ט שנים אם ט הוא מספר שלם, הוא יהפוך ל א (1 + ר ) טלשפשף. לפיכך, מציין אבלהון סופי, תהיה לנו נוסחת הריבית הדריבית הבאה:

אבל = א (1 + ר ) טאיפה ר = ע / 100 .

דוגמא.תן א =2 300 רובל, ע = 4, ט=20 שנים; ואז הנוסחה נותנת:

ר = 4 / 100 = 0,04 ; A \u003d 2 300 (1.04) 20.

לחשב אבל, אנו משתמשים בלוגריתמים:

עֵץ א = log 2 300 + 20 log 1.04 = 3.3617 + 20 0.0170 = 3.3617+0.3400 = 3.7017.

A=5031רוּבָּל.

תגובה.בדוגמה זו, היה לנו יומן 1.04להכפיל ב 20 . מאז המספר 0,0170 יש קירוב יומן 1.04עד ל 1 / 2 חלק עשרת אלפים, ואז המכפלה של מספר זה ב 20 יהיה רק ​​עד 1 / 2 20, כלומר עד 10 עשרת אלפים \u003d אלפית. לכן, בסך הכל 3,7017 איננו יכולים לערוב לא רק לנתון של עשרת אלפים, אלא גם לנתון של אלפיות. על מנת להשיג דיוק רב יותר במקרים כאלה, עדיף למספר 1 + ר קח לוגריתמים לא בני 4 ספרות, אלא עם מספר רב של ספרות, למשל. 7 ספרות. לשם כך, אנו מספקים כאן טבלה קטנה שבה נכתבים לוגריתמים בני 7 ספרות עבור הערכים הנפוצים ביותר. ר .

290. המשימה העיקרית לתשלומים דחופים.מישהו לקח א רובל עבור ר % עם התנאי לפירעון החוב, בצירוף הריבית המגיעה עליו, ב ט שנים, משלמים את אותו הסכום בסוף כל שנה. מה הסכום הזה צריך להיות?

סְכוּם איקס המשולם מדי שנה בתנאים כאלה נקרא תשלום דחוף. בוא נסמן שוב ר כסף ריבית שנתית מ 1 רובל, כלומר, המספר ע / 100 . ואז עד סוף השנה הראשונה החוב א עולה ל א (1 + ר ), אחרי תשלום איקס רובל זה ייעשה א (1 + ר )-איקס .

עד סוף השנה השנייה, כל רובל מסכום זה יהפוך שוב ל 1 + ר רובל, ולכן החוב יהיה [ א (1 + ר )-איקס ](1 + ר ) = א (1 + ר ) 2 - איקס (1 + ר ), ולתשלום איקס רובל יהיה: א (1 + ר ) 2 - איקס (1 + ר ) - איקס . כך גם נוודא שעד סוף השנה ה-3 החוב יהיה

א (1 + ר ) 3 - איקס (1 + ר ) 2 - איקס (1 + ר ) - איקס ,

ובכלל והסוף ט השנה תהיה:

א (1 + ר ) ט - איקס (1 + ר ) t-1 - איקס (1 + ר ) t-2 ... - איקס (1 + ר ) - איקס , או

א (1 + ר ) ט - איקס [ 1 + (1 + ר ) + (1 + ר ) 2 + ...+ (1 + ר ) t-2 + (1 + ר ) t-1 ]

הפולינום בתוך הסוגריים מייצג את סכום האיברים של ההתקדמות הגיאומטרית; שיש לו את החבר הראשון 1 , אחרון ( 1 + ר ) t-1, והמכנה ( 1 + ר ). על פי הנוסחה לסכום איברי התקדמות גיאומטרית (סעיף 10 פרק 3 § 249) אנו מוצאים:

וסכום החוב שאחרי ט התשלום החמישי יהיה:

לפי מצב הבעיה, החוב בסוף ט השנה ה' צריכה להיות שווה ל 0 ; בגלל זה:

איפה

כאשר מחשבים זאת נוסחאות תשלום דחופותבאמצעות לוגריתמים, עלינו למצוא תחילה מספר עזר נ = (1 + ר ) טלפי לוגריתם: logN= טיומן (1+ ר) ; מִמצָא נ, נחסר ממנו 1, ואז נקבל את המכנה של הנוסחה עבור איקס, לאחר מכן, לפי הלוגריתם המשני, אנו מוצאים:

עֵץ איקס= יומן א+ log N + log r - log (N - 1).

291. משימה עיקרית לתרומות דחופות.מישהו מפקיד אותו סכום לבנק בתחילת כל שנה א לשפשף. קבע איזה הון נוצר מהתרומות האלה לאחר מכן ט שנים אם הבנק ישלם ר רבית דרבית.

מציין דרך ר כסף ריבית שנתית מ 1 רובל, כלומר. ע / 100 , אנו טוענים כדלקמן: עד סוף השנה הראשונה, ההון יהיה א (1 + ר );

בתחילת שנה ב' יתווסף סכום זה א רובל; זה אומר שבזמן הזה הבירה תהיה א (1 + ר ) + א . עד סוף שנה 2 הוא יעשה זאת א (1 + ר ) 2 + א (1 + ר );

בתחילת השנה השלישית מוצג שוב א רובל; זה אומר שבזמן הזה הבירה תהיה א (1 + ר ) 2 + א (1 + ר ) + א ; עד סוף ה-3 הוא יהיה א (1 + ר ) 3 + א (1 + ר ) 2 + א (1 + ר ) בהמשך לשיקולים אלו, אנו מוצאים שעד הסוף ט שנה נדרשת הון איהיה:

זוהי הנוסחה לתרומות לתקופה קצובה הניתנות בתחילת כל שנה.

ניתן לקבל את אותה נוסחה על ידי ההיגיון הבא: הפרק הראשון ב א רובל בזמן בבנק ט שנים, יהפוך, על פי נוסחת הריבית דריבית, ל א (1 + ר ) טלשפשף. התשלום השני, להיות בבנק שנה פחות, כלומר. ט - 1 שנים, צור קשר א (1 + ר ) t-1לשפשף. באופן דומה, הפרק השלישי ייתן א (1 + ר ) t-2וכו', ולבסוף, התשלום האחרון, להיות בבנק רק שנה, יפנה א (1 + ר ) לשפשף. אז הבירה הסופית אלשפשף. יהיה:

א= א (1 + ר ) ט + א (1 + ר ) t-1 + א (1 + ר ) t-2 + . . . + א (1 + ר ),

אשר, לאחר פישוט, נותן את הנוסחה שנמצאה למעלה.

בעת חישוב באמצעות הלוגריתמים של נוסחה זו, עליך לעשות את אותו הדבר כמו בעת חישוב הנוסחה לתשלומים דחופים, כלומר, תחילה למצוא את המספר N = ( 1 + ר ) טלפי הלוגריתם שלו: logN= טעֵץ(1 + ר ), ואז מספר N-1ואז קח את הלוגריתם של הנוסחה:

log A = log א+ יומן (1+ ר) + לוג (N - 1) - 1 וגר

תגובה.אם התרומה הדחופה ל א לשפשף. בוצע לא בתחילתה, אלא בסוף כל שנה (כמו למשל, תשלום דחוף איקס כדי להחזיר את החוב), ואז, בטענה כמו הקודם, אנחנו מוצאים את זה בסוף ט שנה נדרשת הון אבל"לשפשף. יהיה (כולל הפרק האחרון א לשפשף., לא נושא ריבית):

א"= א (1 + ר ) t-1 + א (1 + ר ) t-2 + . . . + א (1 + ר ) + א

ששווה ל:

כְּלוֹמַר אבל"מופיע ב ( 1 + ר ) פעמים פחות אבל, שהיה צפוי, מאז כל רובל הון אבל"שוכב בבנק במשך שנה פחות מהרובל ההון המקביל אבל.