Taylori seeria elementaarfunktsioonide laiendamine. Taylori laienemine
Kui funktsioonil f(x) on mingil intervallil, mis sisaldab punkti a, on tuletised kõigist järkudest, siis saab sellele rakendada Taylori valemit:
,
Kus rn- nn jääktermin või seeria ülejäänud osa, seda saab hinnata Lagrange'i valemi abil:
, kus arv x asub x ja a vahel.
Funktsioonide sisestamise reeglid:
Kui mõne väärtuse eest X rn→0 kl n→∞, siis limiidis muutub Taylori valem selle väärtuse jaoks koonduvaks Taylori sari:
,
Seega saab funktsiooni f(x) vaadeldavas punktis x laiendada Taylori seeriaks, kui:
1) tal on kõikide järjekordade tuletised;
2) konstrueeritud jada selles punktis koondub.
Kui a = 0 saame rea nimega Maclaurini lähedal:
,
Maclaurini seeria kõige lihtsamate (elementaarsete) funktsioonide laiendamine:
eksponentsiaalsed funktsioonid
, R=∞
Trigonomeetrilised funktsioonid ![]() , R=∞
, R=∞ ![]() , R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funktsioon actgx ei laiene x astmetes, sest ctg0=∞
Hüperboolsed funktsioonid
Logaritmilised funktsioonid
, -1
Binoomjada
![]() .
.
Näide nr 1. Laiendage funktsioon astmeseeriaks f(x)= 2x.
Lahendus. Leiame funktsiooni ja selle tuletiste väärtused aadressil X=0
f(x) = 2x, f( 0)
= 2 0
=1;
f"(x) = 2x ln2, f"( 0)
= 2 0
ln2=ln2;
f""(x) = 2x 2 2, f""( 0)
= 2 0
log 2 2 = log 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0)
= 2 0
ln n 2 = ln n 2.
Asendades saadud tuletiste väärtused Taylori seeria valemiga, saame:
Selle seeria lähenemisraadius on võrdne lõpmatusega, nii et see laiendus kehtib -∞<x<+∞.
Näide nr 2. Kirjutage Taylori seeria võimsustes ( X+4) funktsiooni jaoks f(x)= e x.
Lahendus. Funktsiooni e tuletiste leidmine x ja nende väärtused hetkel X=-4.
f(x)= e x, f(-4)
= e -4
;
f"(x)= e x, f"(-4)
= e -4
;
f""(x)= e x, f""(-4)
= e -4
;
…
f(n)(x)= e x, f(n)( -4)
= e -4
.
Seetõttu on funktsiooni soovitud Taylori seeria vorm:
See laiendus kehtib ka -∞ korral<x<+∞.
Näide nr 3. Laienda funktsiooni f(x)=ln x kraadide kaupa ( X- 1),
(st Taylori seerias punkti läheduses X=1).
Lahendus. Leiame selle funktsiooni tuletised.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f(n)=(- 1) n-1 (n-1)!
Asendades need väärtused valemisse, saame soovitud Taylori seeria:
D'Alemberti testi abil saab kontrollida, et seeria koondub ½x-1½<1 . Действительно,
Seeria koondub, kui ½ X- 1½<1, т.е. при 0<x<2. При X=2 saame vahelduva jada, mis vastab Leibnizi testi tingimustele. Kui x=0 on funktsioon määratlemata. Seega on Taylori rea konvergentsi piirkonnaks poolavatud intervall (0;2]).
Näide nr 4. Laiendage funktsiooni võimsusreas. Näide number 5. Laiendage funktsiooni Maclaurini seerias. Kommenteeri
.
See meetod põhineb teoreemil funktsiooni laiendamise kordumatuse kohta astmereas. Selle teoreemi olemus seisneb selles, et sama punkti läheduses ei ole võimalik saada kahte erinevat astmerida, mis läheneksid samale funktsioonile, olenemata sellest, kuidas selle laiendamine toimub. Näide nr 5a. Laiendage funktsiooni Maclaurini seerias, märkige lähenemisala. Murdu 3/(1-3x) võib vaadelda lõpmatult kahaneva geomeetrilise progressiooni summana, mille nimetaja on 3x, kui |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Näide number 6. Laiendage funktsiooni Taylori seerias punkti x = 3 läheduses. Näide number 7. Kirjutage funktsiooni ln(x+2) Taylori jada astmetes (x -1). Näide number 8. Laiendage funktsiooni f(x)=sin(πx/4) Taylori reas ümber punkti x =2. Näide nr 1. Arvutage ln(3) täpsusega 0,01. Näide nr 2. Arvutage 0,0001 täpsusega. Näide nr 3. Arvutage integraal ∫ 0 1 4 sin (x) x täpsusega 10 -5 . Näide nr 4. Arvutage integraal ∫ 0 1 4 e x 2 täpsusega 0,001. Kui funktsioon f(x) on mingil intervallil, mis sisaldab punkti A, kõigi järkude tuletised, siis saab sellele rakendada Taylori valemit: Kus rn- nn jääktermin või seeria ülejäänud osa, seda saab hinnata Lagrange'i valemi abil: Kui mõne väärtuse eest x r n®0 kl n®¥, siis limiidis muutub selle väärtuse Taylori valem koonduvaks valemiks Taylori sari: Seega funktsioon f(x) saab vaadeldavas kohas laiendada Taylori seeriaks X, Kui: 1) tal on kõikide järjekordade tuletised; 2) konstrueeritud jada selles punktis koondub. Kell A=0 saame seeria nimega Maclaurini lähedal: Näide 1
f(x)= 2x. Lahendus. Leiame funktsiooni ja selle tuletiste väärtused aadressil X=0 f(x) = 2x, f( 0)
= 2 0
=1; f¢(x) = 2x ln2, f¢( 0)
= 2 0
ln2=ln2; f¢¢(x) = 2x 2 2, f¢¢( 0)
= 2 0
log 2 2 = log 2 2; f(n)(x) = 2x ln n 2, f(n)( 0)
= 2 0
ln n 2 = ln n 2. Asendades saadud tuletiste väärtused Taylori seeria valemiga, saame: Selle seeria lähenemisraadius on võrdne lõpmatusega, nii et see laiendus kehtib -¥<x<+¥. Näide 2
X+4) funktsiooni jaoks f(x)= e x. Lahendus. Funktsiooni e tuletiste leidmine x ja nende väärtused hetkel X=-4. f(x)= e x, f(-4)
= e -4
; f¢(x)= e x, f¢(-4)
= e -4
; f¢¢(x)= e x, f¢¢(-4)
= e -4
; f(n)(x)= e x, f(n)( -4)
= e -4
. Seetõttu on funktsiooni soovitud Taylori seeria vorm: See lagunemine kehtib ka -¥ puhul<x<+¥. Näide 3
. Laienda funktsiooni f(x)=ln x kraadide kaupa ( X- 1), (st Taylori seerias punkti läheduses X=1). Lahendus. Leiame selle funktsiooni tuletised. Asendades need väärtused valemisse, saame soovitud Taylori seeria: D'Alemberti testi abil saab kontrollida, kas seeria läheneb millal ½ X- 1½<1. Действительно, Seeria koondub, kui ½ X- 1½<1, т.е. при 0<x<2. При X=2 saame vahelduva jada, mis vastab Leibnizi testi tingimustele. Kell X=0 funktsioon ei ole määratletud. Seega on Taylori rea konvergentsi piirkonnaks poolavatud intervall (0;2]). Esitagem sel viisil saadud laiendused Maclaurini seerias (st punkti naabruses X=0) mõne elementaarfunktsiooni jaoks: (2) (3) ( nimetatakse viimast laiendust binoomne jada) Näide 4
. Laiendage funktsioon astmeseeriaks Lahendus. Lagundamisel (1) asendame X peal - X 2, saame: Näide 5
. Laiendage funktsiooni Maclaurini seerias Lahendus. Meil on Kasutades valemit (4), saame kirjutada: asemel asendades X valemisse -X, saame: Siit leiame: Sulgude laiendamine, seeria tingimuste ümberkorraldamine ja sarnaste terminite vähendamine, saame See seeria läheneb intervallile (-1;1), kuna see on tuletatud kahest seeriast, millest igaüks koondub selles intervallis. Kommenteeri
. Valemeid (1)-(5) saab kasutada ka Taylori seerias vastavate funktsioonide laiendamiseks, s.t. funktsioonide laiendamiseks positiivsete täisarvude astmetes ( Ha). Selleks on vaja antud funktsioonil sooritada sellised identsed teisendused, et saada üks funktsioonidest (1) - (5), milles selle asemel X maksab k( Ha) m , kus k on konstantne arv, m on positiivne täisarv. Tihti on mugav muutujat muuta t=Ha ja laiendage saadud funktsiooni t suhtes Maclaurini seerias. See meetod illustreerib teoreemi funktsiooni laiendamise kordumatuse kohta astmereas. Selle teoreemi olemus seisneb selles, et sama punkti läheduses ei ole võimalik saada kahte erinevat astmerida, mis läheneksid samale funktsioonile, olenemata sellest, kuidas selle laiendamine toimub. Näide 6
. Laiendage funktsiooni Taylori seerias punkti läheduses X=3. Lahendus. Selle probleemi saab nagu varemgi lahendada Taylori seeria definitsiooni abil, mille jaoks on vaja leida funktsioonide tuletised ja nende väärtused X=3. Siiski on lihtsam kasutada olemasolevat lagunemist (5): Saadud seeria koondub kell Näide 7
. Kirjutage Taylori seeria võimsustes ( X-1) omadused Lahendus. Seeria koondub kell Funktsionaalsete seeriate hulgas on kõige olulisem koht võimsusseeriatel. Võimseeriat nimetatakse jadaks mille liikmed on kasvavate mittenegatiivsete täisarvude astmetena järjestatud astmefunktsioonid x, A c0
, c 1
, c 2
, c n
on konstantsed väärtused. Numbrid c1
, c 2
, c n
- seeria liikmete koefitsiendid, c0
- tasuta liige. Astumusrea tingimused on määratletud tervel arvureal. Tutvume kontseptsiooniga astmeridade konvergentsi piirkond.
See on muutujate väärtuste kogum x mille jaoks seeria koondub. Võimsusridadel on üsna lihtne lähenemispiirkond. Muutuja tegelike väärtuste jaoks x lähenemisala koosneb kas ühest punktist või on teatud intervall (konvergentsi intervall) või langeb kokku kogu teljega Ox
. Asendamisel astmereas väärtused x= 0 saad arvuseeria c0
+0+0+...+0+...
, mis koondub. Seetõttu kl x= 0 koondub mis tahes astmerida ja seetõttu selle lähenemisala
ei saa olla tühi komplekt. Kõigi astmeridade konvergentsipiirkonna struktuur on sama. Selle saab kindlaks teha järgmise teoreemi abil. 1. teoreem (Abeli teoreem). Kui astmerida koondub mingile väärtusele x = x 0
, mis erineb nullist, siis see läheneb ja pealegi absoluutselt kõigi väärtuste puhul |x| < |x 0
|
. Pange tähele: nii algväärtust "x on null" kui ka mis tahes "x" väärtust, mida võrreldakse algväärtusega, võetakse modulo – märki arvesse võtmata. Tagajärg. Kui võimsusseeria lahkneb
mingis väärtuses x = x 1
, siis see erineb kõigi väärtuste puhul |x| > |x 1
|
. Nagu me varem teada saime, koonduvad kõik astmeridad väärtuse suhtes x= 0. On astmeridu, mis koonduvad ainult jaoks x= 0 ja muude väärtuste puhul lahknevad X. Jättes selle juhtumi vaatlusest välja, eeldame, et astmerida läheneb mingile väärtusele x = x 0
, erineb nullist. Siis koondub see Abeli teoreemi kohaselt intervalli ]-| kõikides punktides x0
|, |x 0
|[
(intervall, mille vasak ja parem piir on x väärtused, mille juures astmerida koondub, võttes vastavalt miinusmärgiga ja plussmärgiga), sümmeetriline alguspunkti suhtes. Kui võimsusjada mingis väärtuses lahkneb x = x 1
, siis lahkneb see Abeli teoreemi järelduvuse põhjal ka kõikides punktides väljaspool lõiku [-| x1
|, |x 1
|]
. Sellest järeldub, et iga astmerea jaoks on alguspunkti suhtes sümmeetriline intervall, mida nimetatakse konvergentsi intervall
, igas punktis, mille jada koondub, võib koonduda piiridel või lahkneda, ja mitte tingimata samaaegselt, vaid väljaspool lõiku, seeria lahkneb. Number R nimetatakse astmeridade lähenemisraadiuseks. Erijuhtudel astmeridade konvergentsi intervall
võib degenereeruda punktini (siis seeria koondub ainult x= 0 ja eeldatakse, et R= 0) või esindavad tervet arvjoont (siis seeria koondub arvjoone kõikidesse punktidesse ja eeldatakse, et ). Seega on astmerea konvergentsipiirkonna määratlus selle määramiseks lähenemisraadius
R ja konvergentsivahemiku piiridel olevate ridade konvergentsi uurimine (for ). 2. teoreem. Kui kõik astmerea koefitsiendid, alates teatud ühest, on nullist erinevad, siis on selle lähenemisraadius võrdne rea üldiste järgnevate liikmete koefitsientide absoluutväärtuste suhte piiriga, s.o. Näide 1. Leidke astmerea konvergentsipiirkond Lahendus. Siin Kasutades valemit (28), leiame selle seeria lähenemisraadiuse: Uurime ridade konvergentsi lähenemisintervalli otstes. Näide 13 näitab, et see seeria läheneb x= 1 ja lahkneb juures x= -1. Seetõttu on lähenemispiirkonnaks poolintervall. Näide 2. Leidke astmerea konvergentsi piirkond Lahendus. Seeria koefitsiendid on positiivsed ja Leiame selle suhte piiri, s.o. võimsusrea lähenemisraadius: Uurime jada konvergentsi intervalli otstes. Väärtuste asendus x= -1/5 ja x= 1/5 selles seerias annab: Esimene neist seeriatest läheneb (vt näide 5). Kuid siis lõigu "Absoluutne lähenemine" teoreemi kohaselt koondub ka teine seeria ja selle koondumispiirkond on segment Näide 3. Leidke astmerea konvergentsi piirkond Lahendus. Siin Valemi (28) abil leiame jada lähenemisraadiuse: Uurime väärtuste jadade konvergentsi. Asendades need selles seerias vastavalt, saame Mõlemad seeriad lahknevad, kuna vajalik konvergentsitingimus ei ole täidetud (nende ühised tingimused ei kipu juures nulli minema). Seega see jada lähenemisintervalli mõlemas otsas lahkneb ja selle lähenemispiirkond on intervall . Näide 5. Leidke astmerea konvergentsi piirkond Lahendus. Leiame seose , kus , ja Vastavalt valemile (28) selle jada lähenemisraadius see tähendab, et seeria koondub ainult siis, kui x= 0 ja erineb teiste väärtuste puhul X. Näited näitavad, et seeriad käituvad lähenemisintervalli otstes erinevalt. Näites 1 seeria koondub lähenemisintervalli ühes otsas ja lahkneb teises, näites 2 koondub mõlemas otsas, näites 3 lahkneb mõlemas otsas. Astumusrea lähenemisraadiuse valem saadakse eeldusel, et kõik jada liikmete koefitsiendid, alates mõnest, on nullist erinevad. Seetõttu on valemi (28) kasutamine lubatud ainult nendel juhtudel. Kui seda tingimust rikutakse, tuleks astmeridade lähenemisraadiust otsida kasutades d'Alemberti märk, või muutes muutujat, teisendades seeria sellisele kujule, milles määratud tingimus on täidetud. Näide 6. Leidke astmerea konvergentsi intervall Lahendus. See seeria ei sisalda paaritu kraadiga termineid X. Seetõttu teisendame seeria sättega . Siis saame sarja mille konvergentsiraadiuse leidmiseks saab kasutada valemit (28). Kuna , ja , siis selle seeria lähenemisraadius Võrdsuselt saame Seega see seeria koondub intervallile . Olgu võimsusseeria jaoks lähenemisraadius R> 0, st. see seeria läheneb intervallile . Siis iga väärtus X konvergentsi intervallist vastab mõnele rea summale. Seetõttu on astmeridade summa funktsioon X konvergentsi intervalli kohta. Tähistades seda läbi f(x), saame kirjutada võrdsuse mõista seda selles mõttes, et seeriate summa igas punktis X konvergentsi intervallist on võrdne funktsiooni väärtusega f(x) sel hetkel. Samas tähenduses ütleme, et astmerida (29) läheneb funktsioonile f(x) lähenemise intervalli kohta. Väljaspool konvergentsi intervalli pole võrdusel (30) mingit tähendust. Näide 7 Leidke astmeridade summa Lahendus. See on geomeetriline seeria a= 1 ja q= x. Seetõttu on selle summa funktsioon kehtib ainult väärtuste puhul, kuigi funktsioon Saab näidata, et astmeridade summa f(x) on pidev ja diferentseeruv mis tahes intervallil konvergentsivahemiku piires, eriti seeriate lähenemisintervalli mis tahes punktis. Esitame teoreemid astmeridade terminite kaupa diferentseerimise ja integreerimise kohta. 1. teoreem. Lähenemisvahemikus olevat astmerida (30) saab diferentseerida terminite kaupa piiramatu arv kordi ja saadud astmeridadel on sama lähenemisraadius kui algsel jadal ja nende summad on vastavalt võrdsed . 2. teoreem. Võimsusrida (30) saab integreerida terminite kaupa piiramatu arv kordi vahemikus 0 kuni X, kui , ja saadud astmeridadel on sama lähenemisraadius kui algsel seerial ning nende summad on vastavalt võrdsed Laske funktsioonil f(x), mida tahetakse laiendada võimsusreas, s.o. esindama kujul (30): Probleemiks on koefitsientide määramine ……………………………………………….. (31) Eeldades võrdsustes (30) ja (31) X= 0, leiame Asendades leitud avaldised võrdsusega (30), saame Leiame mõne elementaarfunktsiooni Maclaurini seeria laienduse. Näide 8 Laiendage funktsiooni Maclaurini seerias Lahendus. Selle funktsiooni tuletised on samad, mis funktsioonil endal: Seetõttu, millal X= 0 meil on Asendades need väärtused valemiga (32), saame soovitud laienduse: See jada koondub tervele arvujoonele (selle lähenemisraadius on ). Kõrgema matemaatika üliõpilased peaksid teadma, et mõne meile antud jada konvergentsi intervalli kuuluva astmerea summa on pidev ja piiramatu arv kordi diferentseeritud funktsioon. Tekib küsimus: kas on võimalik väita, et antud suvaline funktsioon f(x) on mõne astmerea summa? See tähendab, millistel tingimustel saab funktsiooni f(x) esitada astmereaga? Selle küsimuse tähtsus seisneb selles, et funktsiooni f(x) on võimalik ligikaudu asendada astmerea paari esimese liikme summaga, st polünoomiga. Selline funktsiooni asendamine üsna lihtsa avaldisega - polünoomiga - on mugav ka mõne ülesande lahendamisel, nimelt: integraalide lahendamisel, arvutamisel jne. On tõestatud, et mõne funktsiooni f(x), milles saab arvutada kuni (n + 1)-nda järgu tuletisi, sealhulgas viimast, on mõne funktsiooni (α - R; x 0 + R) läheduses. punkti x = α valem: See valem on oma nime saanud kuulsa teadlase Brook Taylori järgi. Eelmisest saadud seeriat nimetatakse Maclaurini seeriaks: Reegel, mis võimaldab Maclaurini seerias laieneda: R n (x) -> 0 n jaoks -> lõpmatus. Kui selline on olemas, peab selles sisalduv funktsioon f(x) ühtima Maclaurini rea summaga. Mõelge nüüd Maclaurini seeriale üksikute funktsioonide jaoks. 1. Seega esimene on f(x) = e x. Loomulikult on sellisel funktsioonil vastavalt oma omadustele väga erineva järgu tuletised ja f (k) (x) \u003d e x, kus k võrdub kõigega. Asendame x \u003d 0. Saame f (k) (0) \u003d e 0 \u003d 1, k \u003d 1,2 ... Eelneva põhjal näeb seeria e x välja järgmine: 2. Maclaurini seeria funktsiooni f(x) = sin x jaoks. Selgitage kohe, et kõigi tundmatute funktsioonil on lisaks f "(x) \u003d cos x \u003d sin (x + n / 2), f "" (x) \u003d -sin x \u003d sin (x +) tuletised. 2*n/2)..., f(k)(x)=sin(x+k*n/2), kus k on võrdne mis tahes naturaalarvuga. See tähendab, et lihtsate arvutustega saame järeldada, et jada f(x) = sin x näeb välja selline: 3. Nüüd proovime vaadelda funktsiooni f(x) = cos x. Sellel on suvalises järjekorras tuletised kõigi tundmatute jaoks ja |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так: Niisiis panime kirja kõige olulisemad funktsioonid, mida saab Maclaurini seerias laiendada, kuid mõne funktsiooni puhul on neid täiendatud Taylori seeriaga. Nüüd loetleme need. Samuti väärib märkimist, et Taylori ja Maclaurini seeriad on oluline osa kõrgema matemaatika seeriate lahendamise praktikast. Niisiis, Taylori sari. 1. Esimene on rida f-ii f (x) = ln (1 + x) jaoks. Nagu eelmistes näidetes, saame f (x) = ln (1 + x) korral lisada seeria, kasutades Maclaurini seeria üldkuju. selle funktsiooni jaoks saab aga Maclaurini seeriat saada palju lihtsamalt. Pärast teatud geomeetrilise jada integreerimist saame sellise valimi jaoks rea f (x) = ln (1 + x): 2. Ja teine, mis on meie artiklis lõplik, on seeria f (x) \u003d arctg x jaoks. Intervalli [-1; 1] kuuluva x puhul kehtib laiendus: See on kõik. Selles artiklis käsitleti enim kasutatud Taylori ja Maclaurini seeriaid kõrgemas matemaatikas, eriti majandus- ja tehnikaülikoolides.
Lahendus. Dekompositsioonis (1) asendame x -x 2-ga, saame:
, -∞
Lahendus. Meil on
Kasutades valemit (4), saame kirjutada:
asendades x asemel valemis -x, saame:
Siit leiame: ln(1+x)-ln(1-x) = -
Sulgude laiendamine, seeria tingimuste ümberkorraldamine ja sarnaste terminite vähendamine, saame
. See jada koondub intervallisse (-1;1), kuna see saadakse kahest seeriast, millest igaüks läheneb selles intervallis.
Valemeid (1)-(5) saab kasutada ka Taylori seerias vastavate funktsioonide laiendamiseks, s.t. funktsioonide laiendamiseks positiivsete täisarvude astmetes ( Ha). Selleks on vaja antud funktsioonil sooritada sellised identsed teisendused, et saada üks funktsioonidest (1) - (5), milles selle asemel X maksab k( Ha) m , kus k on konstantne arv, m on positiivne täisarv. Tihti on mugav muutujat muuta t=Ha ja laiendage saadud funktsiooni t suhtes Maclaurini seerias.
Lahendus. Kõigepealt leiame 1-x-6x 2 =(1-3x)(1+2x) , .
algklassidesse:
konvergentsipiirkonnaga |x|< 1/3.
Lahendus. Selle probleemi saab nagu varemgi lahendada Taylori seeria definitsiooni abil, mille jaoks on vaja leida funktsioonide tuletised ja nende väärtused X=3. Siiski on lihtsam kasutada olemasolevat lagunemist (5):
=
Saadud seeria läheneb või -3
Lahendus.
Seeria läheneb väärtusele , või -2< x < 5.
Lahendus. Teeme asenduseks t=x-2:
Kasutades laiendust (3), milles asendame x-ga π / 4 t, saame:
Saadud seeria koondub antud funktsioonile punktis -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Ligikaudsed arvutused võimsusridade abil
Jõuseeriaid kasutatakse laialdaselt ligikaudsetes arvutustes. Nende abiga saate etteantud täpsusega arvutada juurte, trigonomeetriliste funktsioonide, arvude logaritmide, kindlate integraalide väärtusi. Seeriaid kasutatakse ka diferentsiaalvõrrandite integreerimisel.
Mõelge funktsiooni laiendamisele astmereas:
Funktsiooni ligikaudse väärtuse arvutamiseks antud punktis X, mis kuulub näidatud seeria konvergentsi piirkonda, esimene n liikmed ( n on lõplik arv) ja ülejäänud terminid jäetakse kõrvale:
Saadud ligikaudse väärtuse vea hindamiseks on vaja hinnata äravisatud jääki r n (x) . Selleks kasutatakse järgmisi meetodeid:
Lahendus. Kasutame dekompositsiooni , kus x=1/2 (vt eelmise teema näidet 5):
Kontrollime, kas saame ülejäänud kolme laiendusliikme järel kõrvale jätta, selleks hindame seda lõpmatult kahaneva geomeetrilise progressiooni summaga:
Seega võime selle jäägi ära visata ja saada
Lahendus. Kasutame binoomjada. Kuna 5 3 on 130-le lähim täisarvuline kuup, on soovitatav esitada arv 130 kujul 130=5 3 +5. 
kuna Leibnizi testi rahuldav saadud märgi-vaheldusseeria neljas liige on juba nõutavast täpsusest väiksem:
, seega võib selle ja sellele järgnevatest terminitest loobuda.
Paljusid praktiliselt vajalikke kindlaid või ebaõigeid integraale ei saa arvutada Newtoni-Leibnizi valemi abil, kuna selle rakendamine on seotud antiderivaadi leidmisega, millel pole sageli elementaarfunktsioonides avaldist. Samuti juhtub, et antiderivaadi leidmine on võimalik, kuid tarbetult töömahukas. Kui aga integrand on laiendatud astmereaks ja integreerimispiirid kuuluvad selle jada konvergentsi intervalli, siis on integraali ligikaudne arvutamine etteantud täpsusega võimalik.
Lahendus. Vastavat määramatut integraali ei saa väljendada elementaarfunktsioonides, s.t. on "võimatu integraal". Newtoni-Leibnizi valemit ei saa siin rakendada. Arvutame integraali ligikaudselt.
Patu jada termini kaupa x peal x, saame: 
Integreerides selle seeria terminite kaupa (see on võimalik, kuna integreerimise piirid kuuluvad selle seeria lähenemisvahemikku), saame:
Kuna saadud seeria vastab Leibnizi tingimustele ja piisab kahe esimese liikme summast, et saada soovitud väärtus etteantud täpsusega.
Seega leiame  .
.
Lahendus.

![]() . Kontrollime, kas saame pärast saadud seeria teist liiget ülejäänud osa ära visata.
. Kontrollime, kas saame pärast saadud seeria teist liiget ülejäänud osa ära visata.
0,0001<0.001. Следовательно,  .
. , mille vahele jääb arv x X Ja A.
, mille vahele jääb arv x X Ja A.![]()
![]()
![]()
![]()
![]()

![]() ,
,
![]() ,
,![]()
![]()


![]() või -3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.
või -3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.![]() .
.![]() või 2< x 5 naela.
või 2< x 5 naela.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

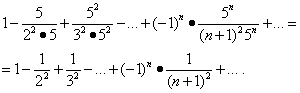
![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Jõuseeria summa. Astmete ridade diferentseerimine ja integreerimine
![]()
![]() . Seeria läheneb, kui , ja on selle lähenemisintervall. Seega võrdsus
. Seeria läheneb, kui , ja on selle lähenemisintervall. Seega võrdsus![]()
![]() määratletud kõigi väärtuste jaoks X, välja arvatud X= 1.
määratletud kõigi väärtuste jaoks X, välja arvatud X= 1.
Funktsioonide laiendamine võimsusridadesse
![]() rida (30). Selleks, eristades võrdsust (30) termini kaupa, leiame järjestikku:
rida (30). Selleks, eristades võrdsust (30) termini kaupa, leiame järjestikku:![]()
![]()


 (32)
(32)
![]() (33)
(33)









