Rozšírenie elementárnych funkcií v Taylorovom rade. Taylorova expanzia
Ak má funkcia f(x) derivácie všetkých rádov na nejakom intervale obsahujúcom bod a, možno na ňu použiť Taylorov vzorec:
,
Kde rn- takzvaný zvyškový člen alebo zvyšok série, možno ho odhadnúť pomocou Lagrangeovho vzorca:
, kde číslo x leží medzi x a a.
Pravidlá zadávania funkcií:
Ak pre nejakú hodnotu X rn→0 o hod n→∞, potom sa v limite Taylorov vzorec pre túto hodnotu zmení na konvergentný Taylorova séria:
,
Funkciu f(x) je teda možné rozšíriť na Taylorov rad v uvažovanom bode x, ak:
1) má deriváty všetkých rádov;
2) zostrojený rad v tomto bode konverguje.
Pre a = 0 dostaneme rad tzv neďaleko Maclaurinu:
,
Rozšírenie najjednoduchších (elementárnych) funkcií v rade Maclaurin:
exponenciálne funkcie
R = ∞
Goniometrické funkcie ![]() R = ∞
R = ∞ ![]() R = ∞
R = ∞
, (-π/2< x < π/2), R=π/2
Funkcia actgx sa nerozpína v mocninách x, pretože ctg0=∞
Hyperbolické funkcie
Logaritmické funkcie
, -1
Binomický rad
![]() .
.
Príklad #1. Rozbaľte funkciu na mocninový rad f(x)= 2X.
Riešenie. Nájdeme hodnoty funkcie a jej derivátov na X=0
f(x) = 2X, f( 0)
= 2 0
=1;
f"(x) = 2X ln2, f"( 0)
= 2 0
ln2=ln2;
f""(x) = 2X V 22, f""( 0)
= 2 0
log 2 2= log 2 2;
…
f(n)(x) = 2X ln n 2, f(n)( 0)
= 2 0
ln n 2 = ln n 2.
Nahradením získaných hodnôt derivátov do vzorca Taylorovho radu dostaneme:
Polomer konvergencie tohto radu sa rovná nekonečnu, takže toto rozšírenie platí pre -∞<X<+∞.
Príklad č. 2. Napíšte Taylorovu sériu v mocninách ( X+4) pre funkciu f(x)= e X.
Riešenie. Hľadanie derivácií funkcie e X a ich hodnoty v bode X=-4.
f(x)= e X, f(-4)
= e -4
;
f"(x)= e X, f"(-4)
= e -4
;
f""(x)= e X, f""(-4)
= e -4
;
…
f(n)(x)= e X, f(n)( -4)
= e -4
.
Preto požadovaný Taylorov rad funkcie má tvar:
Toto rozšírenie platí aj pre -∞<X<+∞.
Príklad č. 3. Rozbaliť funkciu f(x)=ln X v sérii podľa stupňov ( X- 1),
(t. j. v Taylorovom rade v blízkosti bodu X=1).
Riešenie. Nájdeme deriváty tejto funkcie.
f(x)=lnx , , , ,
f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f(n)=(- 1) n-1 (n-1)!
Nahradením týchto hodnôt do vzorca získame požadovaný Taylorov rad:
Pomocou d'Alembertovho testu je možné overiť, že séria konverguje pri ½x-1½<1 . Действительно,
Rad konverguje, ak ½ X- 1½<1, т.е. при 0<X<2. При X=2 získame striedavý rad, ktorý spĺňa podmienky Leibnizovho testu. Pre x=0 funkcia nie je definovaná. Oblasť konvergencie Taylorovho radu je teda polootvorený interval (0;2].
Príklad č. 4. Rozbaľte funkciu v mocninnom rade. Príklad číslo 5. Rozšírte funkciu v sérii Maclaurin. Komentujte
.
Táto metóda je založená na teoréme o jedinečnosti expanzie funkcie v mocninnom rade. Podstatou tejto vety je, že v blízkosti toho istého bodu nemožno získať dva rôzne mocninné rady, ktoré by konvergovali k tej istej funkcii, bez ohľadu na to, ako sa jej expanzia vykonáva. Príklad č. 5a. Rozbaľte funkciu v sérii Maclaurin a označte oblasť konvergencie. Zlomok 3/(1-3x) možno považovať za súčet nekonečne klesajúcej geometrickej postupnosti s menovateľom 3x, ak |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд
Príklad číslo 6. Rozviňte funkciu v Taylorovom rade v blízkosti bodu x = 3. Príklad číslo 7. Napíšte Taylorov rad v mocninách (x -1) funkcie ln(x+2) . Príklad číslo 8. Rozviňte funkciu f(x)=sin(πx/4) v Taylorovom rade okolo bodu x =2. Príklad #1. Vypočítajte ln(3) s presnosťou 0,01. Príklad č. 2. Vypočítajte s presnosťou na 0,0001. Príklad č. 3. Vypočítajte integrál ∫ 0 1 4 sin (x) x s presnosťou 10 -5 . Príklad č. 4. Vypočítajte integrál ∫ 0 1 4 e x 2 s presnosťou 0,001. Ak je funkcia f(x) má na nejakom intervale obsahujúcom bod A, deriváty všetkých rádov, potom naň možno použiť Taylorov vzorec: Kde rn- takzvaný zvyškový člen alebo zvyšok série, možno ho odhadnúť pomocou Lagrangeovho vzorca: Ak pre nejakú hodnotu x r n®0 pri n®¥, potom sa v limite Taylorov vzorec pre túto hodnotu zmení na konvergentný vzorec Taylorova séria: Takže funkcia f(x) možno v uvažovanom bode rozšíriť do Taylorovho radu X, Ak: 1) má deriváty všetkých rádov; 2) zostrojený rad v tomto bode konverguje. O A=0 dostaneme sériu tzv neďaleko Maclaurinu: Príklad 1
f(x)= 2X. Riešenie. Nájdeme hodnoty funkcie a jej derivátov na X=0 f(x) = 2X, f( 0)
= 2 0
=1; f¢(x) = 2X ln2, f¢( 0)
= 2 0
ln2=ln2; f¢¢(x) = 2X V 22, f¢¢( 0)
= 2 0
log 2 2= log 2 2; f(n)(x) = 2X ln n 2, f(n)( 0)
= 2 0
ln n 2 = ln n 2. Nahradením získaných hodnôt derivátov do vzorca Taylorovho radu dostaneme: Polomer konvergencie tohto radu sa rovná nekonečnu, takže toto rozšírenie platí pre -¥<X<+¥. Príklad 2
X+4) pre funkciu f(x)= e X. Riešenie. Hľadanie derivácií funkcie e X a ich hodnoty v bode X=-4. f(x)= e X, f(-4)
= e -4
; f¢(x)= e X, f¢(-4)
= e -4
; f¢¢(x)= e X, f¢¢(-4)
= e -4
; f(n)(x)= e X, f(n)( -4)
= e -4
. Preto požadovaný Taylorov rad funkcie má tvar: Tento rozklad platí aj pre -¥<X<+¥. Príklad 3
. Rozbaliť funkciu f(x)=ln X v sérii podľa stupňov ( X- 1), (t. j. v Taylorovom rade v blízkosti bodu X=1). Riešenie. Nájdeme deriváty tejto funkcie. Nahradením týchto hodnôt do vzorca dostaneme požadovaný Taylorov rad: Pomocou d'Alembertovho testu je možné overiť, že séria konverguje, keď ½ X- 1½<1. Действительно, Rad konverguje, ak ½ X- 1½<1, т.е. при 0<X<2. При X=2 získame striedavý rad, ktorý spĺňa podmienky Leibnizovho testu. O X Funkcia =0 nie je definovaná. Oblasť konvergencie Taylorovho radu je teda polootvorený interval (0;2]. Uveďme takto získané rozšírenia v Maclaurinovom rade (t. j. v okolí bodu X=0) pre niektoré elementárne funkcie: (2) (3) ( posledná expanzia je tzv binomický rad) Príklad 4
. Rozbaľte funkciu na mocninový rad Riešenie. V rozklade (1) nahrádzame X na - X 2, dostaneme: Príklad 5
. Rozšírte funkciu v sérii Maclaurin Riešenie. Máme Pomocou vzorca (4) môžeme napísať: nahradenie namiesto X do vzorca -X, dostaneme: Odtiaľto nájdeme: Dostaneme rozšírenie zátvoriek, preusporiadanie výrazov série a zmenšenie podobných výrazov Tento rad v intervale konverguje (-1;1), pretože je odvodený z dvoch radov, z ktorých každý konverguje v tomto intervale. Komentujte
. Vzorce (1)-(5) možno použiť aj na rozšírenie zodpovedajúcich funkcií v Taylorovom rade, t.j. na rozšírenie funkcií v kladných celých mocninách ( Ha). Na to je potrebné vykonať také identické transformácie na danej funkcii, aby sme získali jednu z funkcií (1) - (5), v ktorej namiesto X náklady k( Ha) m , kde k je konštantné číslo, m je kladné celé číslo. Často je vhodné zmeniť premennú t=Ha a rozšíriť výslednú funkciu vzhľadom na t v Maclaurinovom rade. Táto metóda ilustruje teorém o jedinečnosti expanzie funkcie v mocninnom rade. Podstatou tejto vety je, že v blízkosti toho istého bodu nemožno získať dva rôzne mocninné rady, ktoré by konvergovali k tej istej funkcii, bez ohľadu na to, ako sa jej expanzia vykonáva. Príklad 6
. Rozšírte funkciu v Taylorovom rade v okolí bodu X=3. Riešenie. Tento problém je možné vyriešiť, ako predtým, pomocou definície Taylorovho radu, pre ktorý je potrebné nájsť deriváty funkcií a ich hodnoty na X=3. Bude však jednoduchšie použiť existujúci rozklad (5): Výsledný rad konverguje na Príklad 7
. Napíšte Taylorovu sériu v mocninách ( X-1) vlastnosti Riešenie. Séria konverguje na Medzi funkčnými radmi zaujímajú najdôležitejšie miesto mocenské rady. Mocninný rad sa nazýva rad ktorých členmi sú mocninné funkcie usporiadané do rastúcich nezáporných celých mocnín X, A c0
, c 1
, c 2
, c n
sú konštantné hodnoty. čísla c1
, c 2
, c n
- koeficienty členov série, c0
- voľný člen. Členy mocninového radu sú definované na celej číselnej osi. Zoznámime sa s konceptom oblasť konvergencie mocninných radov.
Toto je množina premenných hodnôt X pre ktoré rad konverguje. Mocninné rady majú pomerne jednoduchú oblasť konvergencie. Pre skutočné hodnoty premennej X oblasť konvergencie pozostáva buď z jedného bodu, alebo je to určitý interval (interval konvergencie), alebo sa zhoduje s celou osou Vôl
. Pri dosadzovaní v mocninnom rade hodnoty X= 0 dostanete číselný rad c0
+0+0+...+0+...
, ktorá konverguje. Preto, kedy X= 0 konverguje akýkoľvek mocninový rad, a preto jeho konvergenčná oblasť
nemôže byť prázdna množina. Štruktúra oblasti konvergencie všetkých mocninných radov je rovnaká. Dá sa určiť pomocou nasledujúcej vety. Veta 1 (Abelova veta). Ak mocninový rad konverguje na nejakej hodnote X = X 0
, ktorá je iná ako nula, potom konverguje, a navyše absolútne, pre všetky hodnoty |X| < |X 0
|
. Poznámka: Počiatočná hodnota "x je nula" a akákoľvek hodnota "x", ktorá sa porovnáva s počiatočnou hodnotou, sa berú modulo - bez zohľadnenia znamienka. Dôsledok. Ak mocninné rady sa rozchádzajú
v nejakej hodnote X = X 1
, potom sa líši pre všetky hodnoty |X| > |X 1
|
. Ako sme už zistili, všetky mocninné rady konvergujú pre hodnotu X= 0. Existujú mocninné rady, ktoré konvergujú len pre X= 0 a rozchádzajú sa pre ostatné hodnoty X. Ak tento prípad vylúčime z úvahy, predpokladáme, že mocninný rad konverguje na nejakej hodnote X = X 0
, odlišný od nuly. Potom podľa Abelovej vety konverguje vo všetkých bodoch intervalu ]-| X0
|, |X 0
|[
(interval, ktorého ľavá a pravá hranica sú hodnoty x, v ktorých mocninný rad konverguje, braný so znamienkom mínus a so znamienkom plus), symetrický podľa pôvodu. Ak sa mocninný rad pri nejakej hodnote rozchádza X = X 1
, potom, na základe následku Abelovej vety, diverguje aj vo všetkých bodoch mimo segmentu [-| X1
|, |X 1
|]
. Z toho vyplýva, že pre každý mocninný rad existuje interval , symetrický vzhľadom na počiatok, tzv interval konvergencie
, v každom bode, v ktorom séria konverguje, môže konvergovať na hraniciach alebo sa môže divergovať, a nie nevyhnutne súčasne, ale mimo segmentu sa séria diverguje. číslo R sa nazýva polomer konvergencie mocninového radu. V špeciálnych prípadoch interval konvergencie mocninových radov
môže degenerovať do bodu (potom séria konverguje iba pre X= 0 a predpokladá sa, že R= 0) alebo predstavujú celú číselnú os (potom rad konverguje vo všetkých bodoch číselnej osi a predpokladá sa, že ). Definícia oblasti konvergencie mocninového radu má teda určiť jeho polomer konvergencie
R a štúdium konvergencie radu na hraniciach intervalu konvergencie (pre ). Veta 2. Ak sú všetky koeficienty mocninového radu, počnúc od určitého, nenulové, potom sa jeho polomer konvergencie rovná limitu pri pomere absolútnych hodnôt koeficientov všeobecných nasledujúcich členov radu, t.j. Príklad 1. Nájdite oblasť konvergencie mocninného radu Riešenie. Tu Pomocou vzorca (28) nájdeme polomer konvergencie tohto radu: Pozrime sa na konvergenciu radu na koncoch intervalu konvergencie. Príklad 13 ukazuje, že tento rad konverguje pre X= 1 a líši sa o X= -1. Preto je oblasťou konvergencie polovičný interval . Príklad 2. Nájdite oblasť konvergencie mocninného radu Riešenie. Koeficienty radu sú kladné a Nájdite hranicu tohto pomeru, t.j. polomer konvergencie mocninových radov: Skúmame konvergenciu radu na koncoch intervalu . Substitúcia hodnôt X= -1/5 a X= 1/5 v tejto sérii dáva: Prvý z týchto radov konverguje (pozri príklad 5). Ale potom, na základe vety z odseku "Absolútna konvergencia", druhá séria tiež konverguje a oblasťou jej konvergencie je segment Príklad 3. Nájdite oblasť konvergencie mocninného radu Riešenie. Tu Pomocou vzorca (28) nájdeme polomer konvergencie radu: Pozrime sa na konvergenciu radu hodnôt. Ich nahradením v tomto rade dostaneme Obidva rady divergujú, pretože nie je splnená podmienka nevyhnutnej konvergencie (ich spoločné členy nemajú tendenciu k nule pri ). Na oboch koncoch konvergenčného intervalu teda tento rad diverguje a oblasťou jeho konvergencie je interval . Príklad 5. Nájdite oblasť konvergencie mocninného radu Riešenie. Nájdeme vzťah , kde , a Podľa vzorca (28) polomer konvergencie tohto radu to znamená, že rad konverguje len vtedy X= 0 a líši sa pre ostatné hodnoty X. Príklady ukazujú, že rad sa na koncoch konvergenčného intervalu správa inak. V príklade 1 séria konverguje na jednom konci konvergenčného intervalu a diverguje na druhom, v príklade 2 konverguje na oboch koncoch, v príklade 3 diverguje na oboch koncoch. Vzorec pre polomer konvergencie mocninového radu sa získa za predpokladu, že všetky koeficienty členov radu, začínajúc od niektorých, sú nenulové. Preto je použitie vzorca (28) prípustné len v týchto prípadoch. Ak je táto podmienka porušená, potom by sa mal pomocou polomeru konvergencie mocninového radu hľadať znak d'Alemberta, alebo vykonaním zmeny premennej, transformáciou série do tvaru, v ktorom je splnená špecifikovaná podmienka. Príklad 6. Nájdite interval konvergencie mocninného radu Riešenie. Táto séria neobsahuje výrazy s nepárnymi stupňami X. Preto sériu transformujeme nastavením . Potom dostaneme sériu vzorec (28) možno použiť na nájdenie polomeru konvergencie ktorého. Od , a , Potom polomer konvergencie tohto radu Z rovnosti, ktorú dostaneme , teda tento rad konverguje k intervalu . Nech je to mocninná séria polomer konvergencie R> 0, t.j. tento rad konverguje k intervalu . Potom každá hodnota X z intervalu konvergencie zodpovedá nejakému súčtu radu. Preto je súčet mocninových radov funkciou X na intervale konvergencie. Označuje to cez f(X), môžeme napísať rovnosť chápanie v tom zmysle, že súčet série v každom bode X z intervalu konvergencie sa rovná hodnote funkcie f(X) v tomto bode. V rovnakom zmysle povieme, že mocninný rad (29) konverguje k funkcii f(X) na intervale konvergencie. Mimo intervalu konvergencie nemá rovnosť (30) žiadny význam. Príklad 7 Nájdite súčet mocninových radov Riešenie. Toto je geometrický rad a= 1 a q= X. Preto je jeho súčet funkciou platí len pre hodnoty, aj keď funkcia Dá sa ukázať, že súčet mocninových radov f(X) je spojitý a diferencovateľný na ľubovoľnom segmente v rámci intervalu konvergencie, najmä v ktoromkoľvek bode intervalu konvergencie radu. Uveďme vety o diferenciácii a integrácii mocninných radov po členoch. Veta 1. Mocninný rad (30) v intervale jeho konvergencie môže byť člen po člen neobmedzený počet krát a výsledný mocninný rad má rovnaký polomer konvergencie ako pôvodný rad a ich súčty sú rovné . Veta 2. Výkonový rad (30) možno integrovať po členoch neobmedzene veľakrát v rozsahu od 0 do X, ak , a výsledný mocninový rad má rovnaký polomer konvergencie ako pôvodný rad a ich súčty sú v tomto poradí rovné Nechajte funkciu f(X), ktorý sa má rozširovať v mocninovom rade, t.j. reprezentovať vo forme (30): Problém je určiť koeficienty ……………………………………………….. (31) Za predpokladu rovnosti (30) a (31) X= 0, zistíme Dosadením nájdených výrazov do rovnosti (30) dostaneme Nájdime rozšírenie Maclaurinovho radu niektorých elementárnych funkcií. Príklad 8 Rozšírte funkciu v sérii Maclaurin Riešenie. Deriváty tejto funkcie sú rovnaké ako samotná funkcia: Preto, kedy X= 0 máme Nahradením týchto hodnôt do vzorca (32) získame požadované rozšírenie: Tento rad konverguje na celej číselnej osi (jeho polomer konvergencie je ). Študenti vyššej matematiky by si mali uvedomiť, že súčet niektorých mocninných radov patriacich do intervalu konvergencie radu, ktorý nám je daný, je spojitá a neobmedzene veľakrát derivovaná funkcia. Vzniká otázka: je možné tvrdiť, že daná ľubovoľná funkcia f(x) je súčtom nejakého mocninného radu? To znamená, za akých podmienok môže byť funkcia f(x) reprezentovaná mocninným radom? Dôležitosť tejto otázky spočíva v tom, že funkciu f(x) je možné približne nahradiť súčtom niekoľkých prvých členov mocninného radu, teda polynómom. Takéto nahradenie funkcie pomerne jednoduchým výrazom - polynómom - je vhodné aj pri riešení niektorých problémov, a to: pri riešení integrálov, pri výpočte atď. Je dokázané, že pre nejakú funkciu f(x), v ktorej možno vypočítať derivácie až do (n + 1) rádu, vrátane posledného, v okolí (α - R; x 0 + R) niektorých bod x = α vzorec: Tento vzorec je pomenovaný po slávnom vedcovi Brookovi Taylorovi. Séria získaná z predchádzajúcej sa nazýva séria Maclaurin: Pravidlo, ktoré umožňuje rozšírenie v sérii Maclaurin: R n (x) -> 0 pre n -> nekonečno. Ak existuje, funkcia f(x) v ňom sa musí zhodovať so súčtom Maclaurinovho radu. Zvážte teraz rad Maclaurin pre jednotlivé funkcie. 1. Takže prvé bude f(x) = e x. Samozrejme, podľa svojich vlastností má takáto funkcia deriváty veľmi odlišných rádov a f (k) (x) \u003d e x, kde k sa rovná všetkému Dosaďte x \u003d 0. Dostaneme f (k) (0) \u003d e 0 \u003d 1, k \u003d 1,2 ... Na základe vyššie uvedeného bude séria e x vyzerať takto: 2. Maclaurinov rad pre funkciu f(x) = sin x. Okamžite objasnite, že funkcia pre všetky neznáme bude mať deriváty, okrem f "(x) \u003d cos x \u003d sin (x + n / 2), f "" (x) \u003d -sin x \u003d sin (x + 2*n/2)..., f(k)(x)=sin(x+k*n/2), kde k sa rovná ľubovoľnému prirodzenému číslu. To znamená, že jednoduchými výpočtami môžeme dospieť k záveru, že séria pre f(x) = sin x bude vyzerať takto: 3. Teraz skúsme zvážiť funkciu f(x) = cos x. Má deriváty ľubovoľného poradia pre všetky neznáme a |f (k) (x)| = |cos(x+k*n/2)|<=1, k=1,2... Снова-таки, произведя определенные расчеты, получим, что ряд для f(х) = cos х будет выглядеть так: Uviedli sme teda najdôležitejšie funkcie, ktoré je možné rozšíriť v sérii Maclaurin, ale pre niektoré funkcie sú doplnené o sériu Taylor. Teraz ich uvedieme. Za zmienku tiež stojí, že Taylorove a Maclaurinove rady sú dôležitou súčasťou nácviku riešenia radov vo vyššej matematike. Takže séria Taylor. 1. Prvý bude riadok pre f-ii f (x) = ln (1 + x). Rovnako ako v predchádzajúcich príkladoch, ak máme f (x) = ln (1 + x), môžeme pridať rad pomocou všeobecného tvaru Maclaurinovho radu. pre túto funkciu sa však séria Maclaurin dá získať oveľa jednoduchšie. Po integrácii určitého geometrického radu dostaneme rad pre f (x) = ln (1 + x) takejto vzorky: 2. A druhá, ktorá bude v našom článku konečná, bude séria pre f (x) \u003d arctg x. Pre x patriace do intervalu [-1; 1] platí rozšírenie: To je všetko. V tomto článku sa uvažuje o najpoužívanejších Taylorových a Maclaurinových radoch vo vyššej matematike, najmä na ekonomických a technických univerzitách.
Riešenie. Pri rozklade (1) nahradíme x -x 2, dostaneme:
, -∞
Riešenie. Máme
Pomocou vzorca (4) môžeme napísať:
dosadením namiesto x vo vzorci -x dostaneme:
Odtiaľto nájdeme: ln(1+x)-ln(1-x) = -
Dostaneme rozšírenie zátvoriek, preusporiadanie výrazov série a zmenšenie podobných výrazov
. Tento rad konverguje v intervale (-1;1), pretože je získaný z dvoch radov, z ktorých každý konverguje v tomto intervale.
Vzorce (1)-(5) možno použiť aj na rozšírenie zodpovedajúcich funkcií v Taylorovom rade, t.j. na rozšírenie funkcií v kladných celých mocninách ( Ha). Na to je potrebné vykonať také identické transformácie na danej funkcii, aby sme získali jednu z funkcií (1) - (5), v ktorej namiesto X náklady k( Ha) m , kde k je konštantné číslo, m je kladné celé číslo. Často je vhodné zmeniť premennú t=Ha a rozšíriť výslednú funkciu vzhľadom na t v Maclaurinovom rade.
Riešenie. Najprv nájdeme 1-x-6x 2 =(1-3x)(1+2x) , .
na základné:
s konvergenčným regiónom |x|< 1/3.
Riešenie. Tento problém je možné vyriešiť, ako predtým, pomocou definície Taylorovho radu, pre ktorý je potrebné nájsť deriváty funkcií a ich hodnoty na X=3. Bude však jednoduchšie použiť existujúci rozklad (5):
=
Výsledný rad konverguje na alebo -3
Riešenie.
Séria konverguje na , alebo -2< x < 5.
Riešenie. Urobme náhradu t=x-2:
Pomocou rozšírenia (3), v ktorom za x dosadíme π / 4 t, dostaneme:
Výsledný rad konverguje k danej funkcii pri -∞< π / 4 t<+∞, т.е. при (-∞
, (-∞Približné výpočty pomocou mocninových radov
Mocninné rady sú široko používané v približných výpočtoch. S ich pomocou môžete s danou presnosťou vypočítať hodnoty koreňov, goniometrické funkcie, logaritmy čísel, určité integrály. Rad sa používa aj pri integrácii diferenciálnych rovníc.
Zvážte rozšírenie funkcie v mocninnom rade:
Vypočítať približnú hodnotu funkcie v danom bode X, patriaci do oblasti konvergencie uvedeného radu, prvý nčlenovia ( n je konečné číslo) a zvyšné členy sa vynechajú:
Pre odhad chyby získanej približnej hodnoty je potrebné odhadnúť vyradené reziduum r n (x) . Na tento účel sa používajú nasledujúce metódy:
Riešenie. Použime rozklad , kde x=1/2 (pozri príklad 5 v predchádzajúcej téme):
Pozrime sa, či môžeme zahodiť zvyšok po prvých troch členoch expanzie, preto ho vyhodnotíme pomocou súčtu nekonečne klesajúcej geometrickej postupnosti:
Takže môžeme tento zvyšok zahodiť a získať
Riešenie. Použime binomický rad. Keďže 5 3 je najbližšia celočíselná kocka k 130, odporúča sa reprezentovať číslo 130 ako 130=5 3 +5. 
keďže štvrtý člen získanej série so striedavým znamienkom, ktorý vyhovuje Leibnizovmu testu, je už menší ako požadovaná presnosť:
, takže ho a nasledujúce výrazy možno zahodiť.
Mnoho prakticky potrebných určitých alebo nevlastných integrálov nemožno vypočítať pomocou Newton-Leibnizovho vzorca, pretože jeho aplikácia je spojená s hľadaním primitívnej derivácie, ktorá často nemá výraz v elementárnych funkciách. Stáva sa aj to, že hľadanie primitívnej látky je možné, ale zbytočne prácne. Ak je však integrand rozšírený do mocninového radu a integračné limity patria do intervalu konvergencie tohto radu, potom je možný približný výpočet integrálu s vopred stanovenou presnosťou.
Riešenie. Príslušný neurčitý integrál nemožno vyjadriť v elementárnych funkciách, t.j. je „nemožný integrál“. Tu nemožno použiť Newtonov-Leibnizov vzorec. Vypočítajme približne integrál.
Rozdelenie pojmov podľa pojmov série pre hriech X na X, dostaneme: 
Integrovaním tohto radu člen po člene (to je možné, pretože limity integrácie patria do intervalu konvergencie tohto radu), dostaneme:
Keďže výsledný rad spĺňa Leibnizove podmienky a na získanie požadovanej hodnoty s danou presnosťou stačí zobrať súčet prvých dvoch členov.
Tak zistíme  .
.
Riešenie.

![]() . Skontrolujeme, či môžeme zahodiť zvyšok po druhom člene výsledného radu.
. Skontrolujeme, či môžeme zahodiť zvyšok po druhom člene výsledného radu.
0,0001<0.001. Следовательно,  .
. , kde číslo x je uzavreté medzi X A A.
, kde číslo x je uzavreté medzi X A A.![]()
![]()
![]()
![]()
![]()

![]() ,
,
![]() ,
,![]()
![]()


![]() alebo -3<X- 3<3, 0<X< 6 и является искомым рядом Тейлора для данной функции.
alebo -3<X- 3<3, 0<X< 6 и является искомым рядом Тейлора для данной функции.![]() .
.![]() , alebo 2< X 5 £.
, alebo 2< X 5 £.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

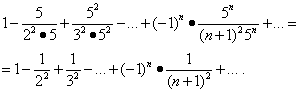
![]()
![]()
![]()
![]()
![]() :
:![]()
![]() ,
,![]()
![]()
![]()
Súčet mocninových radov. Diferenciácia a integrácia mocninových radov
![]()
![]() . Rad konverguje, ak , a je jeho intervalom konvergencie. Preto rovnosť
. Rad konverguje, ak , a je jeho intervalom konvergencie. Preto rovnosť![]()
![]() definované pre všetky hodnoty X, okrem X= 1.
definované pre všetky hodnoty X, okrem X= 1.
Rozšírenie funkcií do mocninových radov
![]() riadok (30). Aby sme to dosiahli, rozlišovaním rovnosti (30) medzi členmi postupne nájdeme:
riadok (30). Aby sme to dosiahli, rozlišovaním rovnosti (30) medzi členmi postupne nájdeme:![]()
![]()
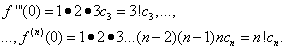

 (32)
(32)
![]() (33)
(33)









