Logaritmide summa samale alusele. Tegevusreegli logaritm logaritmidega

\(a^(b)=c\) \(\Leftparemnool\) \(\log_(a)(c)=b\)

Selgitame seda lihtsamalt. Näiteks \(\log_(2)(8)\) on võrdne võimsusega \(2\), mida tuleb \(8\) saamiseks suurendada. Sellest on selge, et \(\log_(2)(8)=3\).

Näited:		\(\log_(5)(25)=2\)		sest \(5^(2)=25\)
		\(\log_(3)(81)=4\)		sest \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		sest \(2^(-5)=\)\(\frac(1)(32)\)

Logaritmi argument ja alus

Igal logaritmil on järgmine "anatoomia":

Logaritmi argument kirjutatakse tavaliselt selle tasemel ja alus kirjutatakse alamindeksiga, mis on lähemal logaritmi märgile. Ja seda kirjet loetakse järgmiselt: "kahekümne viie logaritm viie baasini."

Kuidas arvutada logaritmi?

Logaritmi arvutamiseks peate vastama küsimusele: mil määral tuleks argumendi saamiseks baasi tõsta?

Näiteks, arvuta logaritm: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\) sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Millise astmeni tuleb \(4\) tõsta, et saada \(16\)? Ilmselgelt teine. Sellepärast:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Millise astmeni tuleb \(\sqrt(5)\) tõsta, et saada \(1\)? Ja mis aste teeb igast arvust ühiku? Null, muidugi!

\(\log_(\sqrt(5))(1)=0\)

d) Millise astmeni tuleb \(\sqrt(7)\) suurendada, et saada \(\sqrt(7)\)? Esimeses - mis tahes arv esimeses astmes võrdub iseendaga.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Millise astmeni tuleb \(3\) tõsta, et saada \(\sqrt(3)\)? Me teame, et see on murdarv ja seetõttu on ruutjuur astme \(\frac(1)(2)\) aste.

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Näide : Arvutage logaritm \(\log_(4\sqrt(2))(8)\)

Lahendus :

\(\log_(4\sqrt(2))(8)=x\)		Peame leidma logaritmi väärtuse, tähistame seda kui x. Nüüd kasutame logaritmi definitsiooni: \(\log_(a)(c)=b\) \(\Nool vasakule\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Mis seob \(4\sqrt(2)\) ja \(8\)? Kaks, sest mõlemat numbrit saab esitada kahega: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		Vasakul kasutame kraadi atribuute: \(a^(m)\cdot a^(n)=a^(m+n)\) ja \((a^(m))^(n)=a ^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Alused on võrdsed, jätkame näitajate võrdsusega
\(\frac(5x)(2)\) \(=3\)		Korrutage võrrandi mõlemad pooled arvuga \(\frac(2)(5)\)
		Saadud juur on logaritmi väärtus

Vastus : \(\log_(4\sqrt(2))(8)=1,2\)

Miks leiutati logaritm?

Selle mõistmiseks lahendame võrrandi: \(3^(x)=9\). Võrdõiguslikkuse toimimiseks sobitage lihtsalt \(x\). Muidugi, \(x=2\).

Nüüd lahendage võrrand: \(3^(x)=8\. Millega x võrdub? Selles ongi asja mõte.

Kõige geniaalsem ütleb: "X on natuke vähem kui kaks." Ja kuidas seda numbrit täpselt kirjutada? Sellele küsimusele vastamiseks mõtlesid nad välja logaritmi. Tänu temale saab siin vastuse kirjutada kujul \(x=\log_(3)(8)\).

Tahan rõhutada, et \(\log_(3)(8)\), samuti iga logaritm on vaid arv. Jah, see näeb välja ebatavaline, kuid on lühike. Sest kui sooviksime seda kirjutada kümnendkohana, näeks see välja järgmine: \(1.892789260714.....\)

Näide : lahendage võrrand \(4^(5x-4)=10\)

Lahendus :

\(4^(5x-4)=10\)		\(4^(5x-4)\) ja \(10\) ei saa taandada samale alusele. Nii et siin ei saa te ilma logaritmita hakkama. Kasutame logaritmi definitsiooni: \(a^(b)=c\) \(\Leftrightrow\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		Pöörake võrrandit nii, et x on vasakul
\(5x-4=\log_(4)(10)\)		Enne meid. Liigutage \(4\) paremale. Ja ärge kartke logaritmi, käsitlege seda kui tavalist arvu.
\(5x=\log_(4)(10)+4\)		Jagage võrrand 5-ga
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Siin on meie juur. Jah, see tundub ebatavaline, kuid vastust ei valita.

Vastus : \(\frac(\log_(4)(10)+4)(5)\)

Kümnend- ja naturaallogaritmid

Nagu on öeldud logaritmi definitsioonis, võib selle alus olla mis tahes positiivne arv, välja arvatud üks \((a>0, a\neq1)\). Ja kõigi võimalike aluste hulgas on kaks, mis esinevad nii sageli, et nendega koos olevate logaritmide jaoks leiutati spetsiaalne lühike tähistus:

Naturaalne logaritm: logaritm, mille alus on Euleri arv \(e\) (võrdub ligikaudu \(2,7182818…\)) ja logaritm on kirjutatud kujul \(\ln(a)\).

See on, \(\ln(a)\) on sama mis \(\log_(e)(a)\)

Kümnendlogaritm: Logaritm, mille alus on 10, kirjutatakse \(\lg(a)\).

See on, \(\lg(a)\) on sama mis \(\log_(10)(a)\), kus \(a\) on mingi arv.

Põhiline logaritmiline identiteet

Logaritmidel on palju omadusi. Ühte neist nimetatakse "logaritmiliseks põhiidentiteediks" ja see näeb välja järgmine:

\(a^(\log_(a)(c))=c\)

See omadus tuleneb otseselt määratlusest. Vaatame, kuidas see valem täpselt ilmus.

Tuletage meelde logaritmi lühike definitsioon:

kui \(a^(b)=c\), siis \(\log_(a)(c)=b\)

See tähendab, et \(b\) on sama mis \(\log_(a)(c)\). Siis saame valemis \(a^(b)=c\) \(b\) asemel kirjutada \(\log_(a)(c)\) . Selgus \(a^(\log_(a)(c))=c\) - peamine logaritmiline identiteet.

Ülejäänud logaritmide omadused leiate. Nende abiga saate lihtsustada ja arvutada avaldiste väärtusi logaritmidega, mida on raske otse arvutada.

Näide : leidke avaldise \(36^(\log_(6)(5))\) väärtus

Lahendus :

Vastus : \(25\)

Kuidas kirjutada arv logaritmina?

Nagu eespool mainitud, on iga logaritm vaid arv. Tõsi on ka vastupidi: logaritmina saab kirjutada mis tahes arvu. Näiteks teame, et \(\log_(2)(4)\) on võrdne kahega. Siis saab kahe asemel kirjutada \(\log_(2)(4)\).

Kuid \(\log_(3)(9)\) on samuti võrdne \(2\), nii et võite kirjutada ka \(2=\log_(3) (9)\) . Samamoodi \(\log_(5)(25)\) ja \(\log_(9)(81)\) jne. See tähendab, et selgub

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Seega, kui meil on vaja, saame need kaks kirjutada logaritmina mis tahes alusega kõikjal (isegi võrrandisse, isegi avaldisesse, isegi ebavõrdsusse) - me kirjutame ruudukujulise aluse lihtsalt argumendina.

Sama on kolmikuga – selle saab kirjutada \(\log_(2)(8)\) või \(\log_(3)(27)\) või \(\log_(4)( 64) \) ... Siin kirjutame argumendina kuubi aluse:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

Ja neljaga:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

Ja miinus ühega:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1) )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1) (7)\)\(...\)

Ja ühe kolmandikuga:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Mis tahes arvu \(a\) saab esitada logaritmina alusega \(b\): \(a=\log_(b)(b^(a))\)

Näide : avaldise väärtuse leidmine \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Lahendus :

Vastus : \(1\)

Juhend

Kirjutage antud logaritmiline avaldis üles. Kui avaldis kasutab logaritmi 10, siis selle tähistus lühendatakse ja näeb välja järgmine: lg b on kümnendlogaritm. Kui logaritmi aluseks on arv e, siis kirjutatakse avaldis: ln b on naturaallogaritm. On arusaadav, et mis tahes tulemuseks on aste, milleni tuleb baasarvu tõsta, et saada arv b.

Kahe funktsiooni summa leidmisel tuleb need lihtsalt ükshaaval eristada ja tulemused liita: (u+v)" = u"+v";

Kahe funktsiooni korrutise tuletise leidmisel on vaja korrutada esimese funktsiooni tuletis teisega ja liita teise funktsiooni tuletis, korrutatud esimese funktsiooniga: (u*v)" = u"* v+v"*u;

Kahe funktsiooni jagatise tuletise leidmiseks on vaja dividendi tuletise korrutisest jagajafunktsiooniga lahutada jagaja tuletise korrutis jagajafunktsiooniga ja jagada seda kõike jagaja funktsiooni ruudus. (u/v)" = (u"*v-v"*u)/v^2;

Kui on antud kompleksfunktsioon, siis on vaja korrutada sisemise funktsiooni tuletis ja välimise funktsiooni tuletis. Olgu y=u(v(x)), siis y"(x)=y"(u)*v"(x).

Ülaltoodu abil saate eristada peaaegu kõiki funktsioone. Vaatame siis mõnda näidet:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
Samuti on ülesanded tuletise arvutamiseks punktis. Olgu funktsioon y=e^(x^2+6x+5) antud, tuleb leida funktsiooni väärtus punktist x=1.
1) Leia funktsiooni tuletis: y"=e^(x^2-6x+5)*(2*x +6).

2) Arvutage funktsiooni väärtus antud punktis y"(1)=8*e^0=8

Seotud videod

Kasulikud nõuanded

Õppige elementaartuletiste tabelit. See säästab palju aega.

Allikad:

• konstantne tuletis

Mis vahe on irratsionaalsel võrrandil ja ratsionaalsel võrrandil? Kui tundmatu muutuja on ruutjuure märgi all, peetakse võrrandit irratsionaalseks.

Juhend

Peamine meetod selliste võrrandite lahendamiseks on mõlema poole tõstmise meetod võrrandid ruudu sisse. Kuid. see on loomulik, esimene samm on märgist lahti saada. Tehniliselt pole see meetod keeruline, kuid mõnikord võib see põhjustada probleeme. Näiteks võrrand v(2x-5)=v(4x-7). Mõlema külje ruudustamisel saad 2x-5=4x-7. Sellist võrrandit pole raske lahendada; x=1. Aga numbrit 1 ei anta võrrandid. Miks? Asendage võrrandis ühik x väärtuse asemel. Paremal ja vasakul pool on avaldised, millel pole mõtet, st. Ruutjuure puhul selline väärtus ei kehti. Seetõttu on 1 kõrvaline juur ja seetõttu pole sellel võrrandil juuri.

Seega lahendatakse irratsionaalne võrrand selle mõlema osa ruudustamiseks. Ja pärast võrrandi lahendamist on vaja kõrvalised juured ära lõigata. Selleks asendage leitud juured algse võrrandiga.

Mõelge veel ühele.
2x+vx-3=0
Loomulikult saab seda võrrandit lahendada sama võrrandi abil, mis eelmine. Ülekandeühendid võrrandid, millel pole ruutjuurt, paremale küljele ja seejärel kasutage ruutude meetodit. lahendage saadud ratsionaalne võrrand ja juured. Aga teine, elegantsem. Sisestage uus muutuja; vx=y. Sellest lähtuvalt saate võrrandi nagu 2y2+y-3=0. See on tavaline ruutvõrrand. Leidke selle juured; y1=1 ja y2=-3/2. Järgmisena lahendage kaks võrrandid vx=1; vx \u003d -3/2. Teisel võrrandil pole juuri, esimesest leiame, et x=1. Ärge unustage juurte kontrollimise vajadust.

Identiteedi lahendamine on üsna lihtne. See nõuab identsete teisenduste tegemist kuni eesmärgi saavutamiseni. Seega lahendatakse ülesanne lihtsaimate aritmeetiliste tehete abil.

Sa vajad

• - paber;
• - pastakas.

Juhend

Lihtsamad sellised teisendused on algebralised lühendatud korrutised (näiteks summa ruut (vahe), ruutude vahe, summa (vahe), summa kuup (vahe)). Lisaks on palju trigonomeetrilisi valemeid, mis on sisuliselt samad identiteedid.

Tõepoolest, kahe liikme summa ruut on võrdne esimese ruuduga pluss kahekordne esimese ja teise korrutis pluss teise ruut, see tähendab (a+b)^2= (a+b )(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Lihtsustage mõlemat

Lahenduse üldpõhimõtted

Korrake matemaatilise analüüsi või kõrgema matemaatika õpikust, mis on kindel integraal. Teatavasti on kindla integraali lahend funktsioon, mille tuletis annab integrandi. Seda funktsiooni nimetatakse antiderivatiivseks. Selle põhimõtte järgi konstrueeritakse põhiintegraalid.
Määra integrandi kuju järgi, milline tabeliintegraalidest on antud juhul sobiv. Seda ei ole alati võimalik kohe kindlaks teha. Sageli muutub tabelivorm märgatavaks alles pärast mitut teisendust integrandi lihtsustamiseks.

Muutuja asendusmeetod

Kui integrand on trigonomeetriline funktsioon, mille argumendiks on mõni polünoom, proovige kasutada muutujate muutmise meetodit. Selleks asenda integrandi argumendis olev polünoom mõne uue muutujaga. Uue ja vana muutuja suhte põhjal määrake integreerimise uued piirid. Seda avaldist eristades leidke uus diferentsiaal . Nii saate vana integraali uue vormi, mis on lähedane või isegi vastab mis tahes tabelivormile.

Teist tüüpi integraalide lahendus

Kui integraal on teist tüüpi integraal, integrandi vektorkuju, siis peate kasutama nendelt integraalidelt skalaarsetele liikumiseks reegleid. Üks selline reegel on Ostrogradsky-Gaussi suhe. See seadus võimaldab minna mõne vektorfunktsiooni rootori voolult kolmikintegraalile antud vektorivälja lahknemise kohal.

Integratsiooni piiride asendamine

Pärast antiderivaadi leidmist on vaja integratsiooni piirid asendada. Esmalt asendage ülempiiri väärtus antiderivaadi avaldisega. Saate mõne numbri. Järgmisena lahutage saadud arvust teine ​​​​arv, saadud antiderivaadi alampiir. Kui üheks integreerimispiiriks on lõpmatus, siis selle asendamisel antiderivatiivfunktsiooni tuleb minna piirini ja leida, mille poole avaldis kipub.
Kui integraal on kahe- või kolmemõõtmeline, peate integraali arvutamise mõistmiseks esitama integratsiooni geomeetrilised piirid. Tõepoolest, näiteks kolmemõõtmelise integraali puhul võivad integreerimise piirid olla terved tasapinnad, mis piiravad integreeritavat mahtu.

Logaritmi definitsioon

Arvu b logaritm aluse a suhtes on eksponent, millele tuleb b saamiseks tõsta a.

Arv e matemaatikas on tavaks tähistada piiri, milleni avaldis kaldub

Number e on irratsionaalne arv- ühega võrreldamatu arv, seda ei saa täpselt väljendada ei tervikuna ega murdosana ratsionaalne number.

Kiri e- ladina sõna esimene täht exonere- uhkeldama, sellest ka nimi matemaatikas eksponentsiaalne- eksponentsiaalne funktsioon.

Number e kasutatakse laialdaselt matemaatikas ja kõigis teadustes, kasutades ühel või teisel viisil oma vajaduste rahuldamiseks matemaatilisi arvutusi.

Logaritmid. Logaritmide omadused

Definitsioon: Positiivse arvu b baaslogaritm on astendaja c, milleni tuleb arvu b saamiseks tõsta arv a.

Põhilogaritmiline identiteet:

7) Uuele baasile ülemineku valem:

lna = log e a, e ≈ 2,718…

Ülesanded ja testid teemal „Logaritmid. Logaritmide omadused»

• Logaritmid – olulised teemad matemaatika eksami kordamiseks

Selleteemaliste ülesannete edukaks täitmiseks peate teadma logaritmi määratlust, logaritmide omadusi, logaritmi põhiidentiteeti, kümnend- ja naturaallogaritmide määratlusi. Selle teema peamised ülesannete tüübid on ülesanded logaritmiliste avaldiste arvutamiseks ja teisendamiseks. Vaatleme nende lahendust järgmiste näidete põhjal.

Lahendus: Kasutades logaritmide omadusi, saame

Lahendus: astme omadusi kasutades saame

1) (2 2) log 2 5 =(2 log 2 5) 2 = 5 2 =25

Logaritmide, formulatsioonide ja tõestuste omadused.

Logaritmidel on mitmeid iseloomulikke omadusi. Selles artiklis analüüsime peamisi logaritmide omadused. Siin anname nende formuleeringud, kirjutame üles logaritmide omadused valemite kujul, näitame näiteid nende rakendamisest ja anname ka tõestusi logaritmide omaduste kohta.

Leheküljel navigeerimine.

Logaritmide põhiomadused, valemid

Meeldejäämise ja kasutamise hõlbustamiseks esitleme logaritmide põhiomadused valemite loendina. Järgmises osas anname nende sõnastused, tõendid, kasutusnäited ja vajalikud selgitused.

Ühiku logi omadus: logi a 1=0 iga a>0 korral, a≠1.

Alusega võrdse arvu logaritm: loga a a=1, kui a>0 , a≠1 .

Baasastme logaritmi omadus: log a a p =p , kus a>0 , a≠1 ja p on mis tahes reaalarv.

Kahe positiivse arvu korrutise logaritm: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
ja n positiivse arvu korrutise logaritmi omadus: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 > 0, x 2 > 0, …, xn > 0 .

Privaatne logaritmi omadus: , kus a>0, a≠1, x>0, y>0.

Arvu astme logaritm: log a b p =p log a |b| , kus a>0, a≠1, b ja p on sellised arvud, et b p aste on mõistlik ja b p >0.

Tagajärg: , kus a>0, a≠1, n on naturaalarv, mis on suurem kui üks, b>0 .

Järeldus 1: , a>0, a≠1, b>0, b≠1.

Järeldus 2: , a>0, a≠1, b>0, p ja q on reaalarvud, q≠0, eriti juhul, kui b=a on meil .

Omaduste avaldused ja tõendid

Läheme edasi logaritmide salvestatud omaduste formuleerimise ja tõestamise juurde. Kõik logaritmide omadused on tõestatud logaritmi definitsiooni ja sellest tuleneva logaritmi põhiidentiteedi ning astme omaduste alusel.

Alustame sellest ühtsuse logaritmi omadused. Selle sõnastus on järgmine: ühtsuse logaritm on võrdne nulliga, see tähendab, logi a 1=0 mis tahes a>0 korral a≠1. Tõestus on arusaadav: kuna a 0 =1 iga a korral, mis vastab ülaltoodud tingimustele a>0 ja a≠1 , siis tuleneb logaritmi definitsioonist kohe tõestatav võrduslog a 1=0.

Toome näiteid vaadeldava omaduse rakendamisest: log 3 1=0 , lg1=0 ja .

Liigume edasi järgmise kinnisvara juurde: alusega võrdse arvu logaritm on võrdne ühega, see on, logi a a=1 kui a>0, a≠1. Tõepoolest, kuna a 1 =a iga a korral, siis logaritmi definitsiooni järgi log a a=1 .

Logaritmide selle omaduse kasutamise näited on log 5 5=1 , log 5.6 5.6 ja lne=1 .

Logaritmi alusega võrdse arvu astme logaritm on võrdne eksponendiga. See logaritmi omadus vastab vormi valemile logi a a p =p, kus a>0, a≠1 ja p on mis tahes reaalarv. See omadus tuleneb otseselt logaritmi definitsioonist. Pange tähele, et see võimaldab kohe määrata logaritmi väärtuse, kui on võimalik esitada logaritmi märgi all olevat arvu baasastmena, räägime sellest lähemalt logaritmide arvutamise artiklis.

Näiteks log 2 2 7 =7, log10 -4 =-4 ja .

Kahe positiivse arvu korrutise logaritm x ja y on võrdne nende arvude logaritmide korrutisega: log a (x y)=log a x+log a y, a>0, a≠1. Tõestame korrutise logaritmi omadust. Tulenevalt astme omadustest a log a x + log a y =a log a x a log a y ning kuna põhilogaritmilise identiteedi järgi log a x =x ja log a y =y , siis log a x a log a y =x y . Seega log a x+log a y =x y , kust logaritmi definitsiooni järgi järgneb nõutav võrdus.

Toome näiteid korrutise logaritmi omaduse kasutamisest: log 5 (2 3)=log 5 2+log 5 3 ja .

Korrutise logaritmi omadust saab üldistada positiivsete arvude x 1 , x 2 , …, x n lõpliku arvu n korrutisega kui log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Seda võrdsust saab hõlpsasti tõestada matemaatilise induktsiooni meetodiga.

Näiteks saab korrutise naturaallogaritmi asendada kolme arvude 4 , e ja naturaallogaritmi summaga.

Kahe positiivse arvu jagatise logaritm x ja y on võrdne nende arvude logaritmide vahega. Jagatislogaritmi omadus vastab vormi valemile , kus a>0, a≠1, x ja y on mõned positiivsed arvud. Selle valemi kehtivus on tõestatud nagu korrutise logaritmi valem: kuna , siis logaritmi definitsiooni järgi .

Siin on näide selle logaritmi omaduse kasutamisest: .

Liigume edasi astme logaritmi omadus. Astme logaritm võrdub astendaja ja selle astme aluse mooduli logaritmi korrutisega. Kirjutame selle astme logaritmi omaduse valemi kujul: log a b p =p log a |b|, kus a>0, a≠1, b ja p on sellised arvud, et b p aste on mõistlik ja b p >0.

Esmalt tõestame selle omaduse positiivse b jaoks. Põhilogaritmiline identiteet võimaldab meil esitada arvu b kui log a b, siis b p =(a log a b) p ja saadud avaldis on võimsusomaduse tõttu võrdne a p log a b . Seega jõuame võrrandini b p =a p log a b, millest logaritmi definitsiooni järgi järeldame, et log a b p =p log a b .

Jääb üle tõestada see omadus negatiivse b jaoks. Siinkohal märgime, et negatiivse b avaldis log a b p on mõttekas ainult paarisaste p kohta (kuna astme b p väärtus peab olema suurem kui null, muidu pole logaritmil mõtet) ja sel juhul b p =|b| p . Siis b p =|b| p =(a log a |b|) p =a p log a |b| , kust log a b p =p log a |b| .

Näiteks, ja ln(-3) 4 =4 ln|-3|=4 ln3 .

See tuleneb eelmisest kinnistust logaritmi omadus juurest: n-nda astme juure logaritm võrdub murdosa 1/n ja juuravaldise logaritmi korrutisega, st kus a>0, a≠1, n on naturaalarv, mis on suurem kui üks, b>0.

Tõestus põhineb võrdusel (vt murdosaastendajaga astendaja definitsiooni), mis kehtib iga positiivse b korral, ja astme logaritmi omadusel: .

Siin on näide selle atribuudi kasutamisest: .

Nüüd tõestame teisendusvalem logaritmi uueks baasiks lahke . Selleks piisab, kui tõestada võrduslogi c b=log a b log c a kehtivust. Põhilogaritmiline identiteet võimaldab meil esitada arvu b kui log a b, siis log c b=log c a log a b . Jääb üle kasutada astme logaritmi omadust: log c a log a b = log a b log c a . Seega on tõestatud võrdus log c b=log a b log c a, mis tähendab, et on tõestatud ka logaritmi uuele alusele ülemineku valem .

Toome paar näidet selle logaritmide omaduse rakendamisest: ja .

Uuele baasile liikumise valem võimaldab teil liikuda edasi logaritmidega, millel on "mugav" alus. Näiteks saab seda kasutada naturaal- või kümnendlogaritmidele üleminekuks, et saaksite logaritmi väärtuse arvutada logaritmide tabelist. Logaritmi uuele alusele ülemineku valem võimaldab mõnel juhul leida ka antud logaritmi väärtuse, kui on teada mõne logaritmi väärtused teiste alustega.

Sageli kasutatakse vormi c=b logaritmi uuele alusele ülemineku valemi erijuhtu. See näitab, et log a b ja log b a on vastastikku pöördarvud. Näiteks, .

Sageli kasutatakse ka valemit, mis on mugav logaritmi väärtuste leidmisel. Oma sõnade kinnituseks näitame, kuidas selle abil arvutatakse vormi logaritmi väärtus. Meil on . Valemi tõestamiseks piisab, kui kasutada üleminekuvalemit logaritmi a uuele alusele: .

Jääb üle tõestada logaritmide võrdlusomadused.

Kasutame vastupidist meetodit. Oletame, et a 1 >1, a 2 >1 ja a 1 2 ning 0 1 korral log a 1 b≤log a 2 b on tõene. Logaritmide omaduste järgi saab need võrratused ümber kirjutada järgmiselt ja vastavalt ja neist järeldub, et vastavalt log b a 1 ≤log b a 2 ja log b a 1 ≥log b a 2. Siis peavad samade alustega astmete omaduste järgi olema täidetud võrrandid b log b a 1 ≥b log b a 2 ja b log b a 1 ≥b log b a 2 ehk a 1 ≥a 2 . Seega oleme jõudnud vastuoluni tingimusega a 1 2 . See lõpetab tõestuse.

Logaritmide põhiomadused

• Materjalid tunni jaoks
• Laadige alla kõik valemid

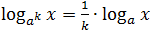
Logaritme, nagu iga arvu, saab igal võimalikul viisil liita, lahutada ja teisendada. Aga kuna logaritmid pole päris tavalised arvud, siis siin kehtivad reeglid, mida kutsutakse põhiomadused.

Neid reegleid tuleb teada – ilma nendeta ei saa lahendada ühtegi tõsist logaritmilist ülesannet. Lisaks on neid väga vähe – ühe päevaga saab kõik selgeks. Nii et alustame.

Logaritmide liitmine ja lahutamine

Vaatleme kahte sama alusega logaritmi: logi a x ja log a y . Seejärel saab neid liita ja lahutada ning:

Seega on logaritmide summa võrdne korrutise logaritmiga ja erinevus on jagatise logaritm. Pange tähele: võtmepunkt siin on - samadel alustel. Kui alused on erinevad, siis need reeglid ei tööta!

Need valemid aitavad arvutada logaritmilist avaldist isegi siis, kui selle üksikuid osi ei arvestata (vt õppetundi "Mis on logaritm"). Vaadake näiteid ja vaadake:

Ülesanne. Leidke avaldise väärtus: log 6 4 + log 6 9.

Kuna logaritmide alused on samad, kasutame summa valemit:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Ülesanne. Leidke avaldise väärtus: log 2 48 − log 2 3.

Alused on samad, kasutame erinevuse valemit:
log 2 48 – log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Ülesanne. Leidke avaldise väärtus: log 3 135 − log 3 5.

Jällegi on alused samad, seega on meil:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Nagu näete, koosnevad algsed avaldised "halbadest" logaritmidest, mida eraldi ei käsitleta. Kuid pärast teisendusi ilmnevad üsna tavalised numbrid. Paljud testid põhinevad sellel faktil. Jah, seda kontrolli – sarnaseid väljendeid täie tõsidusega (mõnikord – praktiliselt ilma muudatusteta) pakutakse eksamil.

Astendaja eemaldamine logaritmist

Teeme nüüd ülesande pisut keerulisemaks. Mis siis, kui logaritmi baasis või argumendis on aste? Seejärel saab selle astme eksponendi logaritmi märgist välja võtta järgmiste reeglite järgi:

• log a x n = n log a x ;
• 
• 

On lihtne mõista, et viimane reegel järgib nende kahte esimest. Kuid parem on see ikkagi meeles pidada - mõnel juhul vähendab see arvutuste mahtu märkimisväärselt.

Loomulikult on kõigil neil reeglitel mõtet, kui järgida ODZ logaritmi: a > 0, a ≠ 1, x > 0. Ja veel üks asi: õppige rakendama kõiki valemeid mitte ainult vasakult paremale, vaid ka vastupidi, s.t. logaritmi endasse saab sisestada arvud enne logaritmi märki. See on see, mida kõige sagedamini nõutakse.

Ülesanne. Leidke avaldise väärtus: log 7 49 6 .

Vabaneme argumendi astmest esimese valemi järgi:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Ülesanne. Leidke avaldise väärtus:

[Joonise pealkiri]

Pange tähele, et nimetaja on logaritm, mille alus ja argument on täpsed astmed: 16 = 2 4 ; 49 = 72. Meil on:

[Joonise pealkiri]

Ma arvan, et viimane näide vajab selgitust. Kuhu kadusid logaritmid? Kuni viimase hetkeni töötame ainult nimetajaga. Nad esitasid seal seisva logaritmi aluse ja argumendi kraadidena ning võtsid välja indikaatorid - nad said “kolmekorruselise” murru.

Vaatame nüüd põhifraktsiooni. Lugejal ja nimetajal on sama arv: log 2 7. Kuna log 2 7 ≠ 0, saame murdosa vähendada - 2/4 jääb nimetajasse. Aritmeetika reeglite järgi saab nelja üle kanda lugejasse, mis ka tehti. Tulemuseks on vastus: 2.

Üleminek uuele vundamendile

Rääkides logaritmide liitmise ja lahutamise reeglitest, rõhutasin konkreetselt, et need töötavad ainult siis, kui alused on samad. Mis siis, kui alused on erinevad? Mis siis, kui need ei ole sama arvu täpsed astmed?

Appi tulevad valemid uuele baasile üleminekuks. Sõnastame need teoreemi kujul:

Olgu antud logaritm log a x. Siis on võrdsus tõene mis tahes arvu c korral, mille puhul c > 0 ja c ≠ 1:

[Joonise pealkiri]

Täpsemalt, kui paneme c = x , saame:

[Joonise pealkiri]

Teisest valemist järeldub, et logaritmi alust ja argumenti on võimalik omavahel vahetada, kuid sel juhul “pööratakse ümber” kogu avaldis, s.t. logaritm on nimetajas.

Neid valemeid leidub tavalistes arvavaldistes harva. Seda, kui mugavad need on, saab hinnata ainult logaritmiliste võrrandite ja võrratuste lahendamisel.

Siiski on ülesandeid, mida ei saa üldse lahendada, välja arvatud uuele sihtasutusele kolimine. Vaatleme paari neist:

Ülesanne. Leidke avaldise väärtus: log 5 16 log 2 25.

Pange tähele, et mõlema logaritmi argumendid on täpsed eksponendid. Võtame välja näitajad: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Nüüd pöörame teise logaritmi ümber:

[Joonise pealkiri]

Kuna korrutis tegurite permutatsioonist ei muutu, korrutasime rahulikult nelja ja kahega ning siis mõtlesime välja logaritmid.

Ülesanne. Leidke avaldise väärtus: log 9 100 lg 3.

Esimese logaritmi alus ja argument on täpsed võimsused. Paneme selle kirja ja vabaneme näitajatest:

[Joonise pealkiri]

Nüüd vabaneme kümnendlogaritmist, liikudes uuele alusele:

[Joonise pealkiri]

Põhiline logaritmiline identiteet

Sageli on lahendamise käigus vaja esitada arv antud baasi logaritmina. Sel juhul aitavad meid valemid:

1. n = log a a n

2. Esimesel juhul saab arvust n argumendi eksponendiks. Arv n võib olla absoluutselt ükskõik milline, sest see on lihtsalt logaritmi väärtus.

   Teine valem on tegelikult parafraseeritud määratlus. Seda nimetataksegi: logaritmiline põhiidentiteet.

   Tõepoolest, mis juhtub, kui arv b tõsta sellise astmeni, et selle astme arv b annab arvu a? Täpselt nii: see on sama number a . Lugege see lõik uuesti hoolikalt läbi – paljud inimesed "ripuvad" selle küljes.

   Nagu uued baasteisendusvalemid, on ka põhilogaritmiline identiteet mõnikord ainus võimalik lahendus.

   [Joonise pealkiri]

   Pange tähele, et log 25 64 = log 5 8 – võtke lihtsalt aluse ruut ja logaritmi argument. Arvestades sama baasiga võimsuste korrutamise reegleid, saame:

   [Joonise pealkiri]

   Kui keegi pole kursis, siis see oli ühtse riigieksami tõeline ülesanne 🙂

   Logaritmiline ühik ja logaritmiline null

   Kokkuvõtteks annan kaks identiteeti, mida on raske omadusteks nimetada – pigem on need logaritmi definitsioonist tulenevad tagajärjed. Neid leitakse pidevalt probleemidest ja üllataval kombel tekitavad nad probleeme isegi "edasijõudnud" õpilastele.

   1. log a a = 1 on logaritmiline ühik. Pidage üks kord meeles: logaritm mis tahes baasile a sellest baasist endast on võrdne ühega.
   2. log a 1 = 0 on logaritmiline null. Alus a võib olla ükskõik milline, aga kui argument on üks - logaritm on null! Kuna a 0 = 1 on definitsiooni otsene tagajärg.

   See on kõik omadused. Harjutage kindlasti nende rakendamist! Laadige tunni alguses petuleht alla, printige see välja – ja lahendage probleemid.

   Logaritm. Logaritmi omadused (liitmine ja lahutamine).

   Logaritmi omadused tuleneb selle määratlusest. Ja nii ka arvu logaritm b põhjusega a defineeritud kui astendaja, milleni arv tuleb tõsta a numbri saamiseks b(logaritm eksisteerib ainult positiivsete arvude puhul).

   Sellest sõnastusest järeldub, et arvutus x=log a b, võrdub võrrandi lahendamisega kirves=b. Näiteks, log 2 8 = 3 sest 8 = 2 3 . Logaritmi sõnastus võimaldab põhjendada, et kui b=a c, siis arvu logaritm b põhjusega a võrdub Koos. Samuti on selge, et logaritmi teema on tihedalt seotud arvu astme teemaga.

   Logaritmidega, nagu kõigi arvudega, saate sooritada liitmise, lahutamise tehted ja muuta igal võimalikul viisil. Kuid arvestades asjaolu, et logaritmid pole päris tavalised arvud, kehtivad siin omad erireeglid, mida nimetatakse põhiomadused.

   Logaritmide liitmine ja lahutamine.

   Võtke kaks logaritmi sama alusega: logi x ja logi a y. Pärast eemaldamist saate teha liitmise ja lahutamise toiminguid:

   Nagu näeme, logaritmide summa võrdub korrutise logaritmiga ja erinevus logaritmid- jagatise logaritm. Ja see on tõsi, kui numbrid a, X ja juures positiivne ja a ≠ 1.

   Oluline on märkida, et nende valemite peamine aspekt on samad alused. Kui alused erinevad üksteisest, siis need reeglid ei kehti!

   Samade alustega logaritmide liitmise ja lahutamise reegleid loetakse mitte ainult vasakult paremale, vaid ka vastupidi. Selle tulemusena on meil teoreemid korrutise logaritmi ja jagatise logaritmi jaoks.

   Toote logaritm kaks positiivset arvu on võrdne nende logaritmide summaga ; parafraseerides seda teoreemi, saame järgmise, kui arvud a, x ja juures positiivne ja a ≠ 1, siis:

   Jagatise logaritm kahe positiivse arvu väärtus on võrdne dividendi ja jagaja logaritmide vahega. Teisisõnu, kui numbrid a, X ja juures positiivne ja a ≠ 1, siis:

   Lahendamisel rakendame ülaltoodud teoreeme näiteid:

   Kui numbrid x ja juures on siis negatiivsed toote logaritmi valem muutub mõttetuks. Seega on keelatud kirjutada:

   kuna avaldised log 2 (-8) ja log 2 (-4) pole üldse määratletud (logaritmiline funktsioon juures= log 2 X defineeritud ainult argumendi positiivsete väärtuste jaoks X).

   Toote teoreem on kohaldatav mitte ainult kahe, vaid ka piiramatu arvu tegurite puhul. See tähendab, et iga loomulik k ja kõik positiivsed numbrid x 1 , x 2 , . . . ,x n on identiteet:

   Alates jagatislogaritmi teoreemid võib saada veel ühe logaritmi omaduse. On hästi teada, et logi a 1 = 0, seega

   Seega on võrdsus:

   Kahe vastastikku pöördarvu logaritmid samal alusel erinevad üksteisest ainult märgi poolest. Niisiis:

   Logaritm. Logaritmide omadused

   Logaritm. Logaritmide omadused

   Kaaluge võrdsust. Andke meile teada väärtused ja me tahame leida selle väärtuse.

   See tähendab, et otsime eksponenti, mille saamiseks peate kukk.

   Lase muutuja võib võtta mis tahes tegeliku väärtuse, siis on muutujatele kehtestatud järgmised piirangud: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Kui teame ja väärtusi ning seisame silmitsi ülesandega leida tundmatu, siis selleks võetakse kasutusele matemaatiline tehe, mida nimetatakse nn. logaritm.

   Et leida väärtus, mida me võtame arvu logaritm peal sihtasutus :

   Arvu logaritm baasile on eksponent, mille saamiseks peate suurendama.

   See on põhilogaritmiline identiteet:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0” title=”b>0”/>

   on sisuliselt matemaatiline tähistus logaritmi määratlused.

   Matemaatilise tehte logaritm on eksponentsiatsiooni pöördväärtus, seega logaritmide omadused on tihedalt seotud kraadi omadustega.

   Loetleme peamised logaritmide omadused:

   (o” title=”a>o”/> , 1” title=”a1”/>, 0” title=”b>0”/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Järgmine omaduste rühm võimaldab teil esitada avaldise eksponenti logaritmi märgi all või logaritmi aluses koefitsiendina enne logaritmi märki:

   6.

   7.

   8.

   9.

   Järgmine valemite rühm võimaldab minna antud alusega logaritmilt suvalise alusega logaritmile ja seda nimetatakse ülemineku valemid uuele alusele:

   10.

   12. (vara 11 tagajärg)

   

   Järgmised kolm omadust pole hästi teada, kuid neid kasutatakse sageli logaritmiliste võrrandite lahendamisel või logaritme sisaldavate avaldiste lihtsustamisel:

   13.

   14.

   15.

   Erijuhtumid:

   — kümnendlogaritm

   — naturaallogaritm

   Logaritme sisaldavate avaldiste lihtsustamisel kasutatakse üldist lähenemist:

   1. Esitame kümnendmurrud tavaliste kujul.

   2. Esitame segaarvud ebaõigete murdudena.

   3. Logaritmi baasil ja logaritmi märgi all olevad arvud jaotatakse algteguriteks.

   4. Püüame viia kõik logaritmid samale alusele.

   5. Rakenda logaritmide omadused.

   Vaatame näiteid logaritme sisaldavate avaldiste lihtsustamisest.

   Näide 1

   Arvutama:

   Lihtsustame kõiki eksponente: meie ülesandeks on viia need logaritmidesse, mille baas on sama, mis eksponendi alus.

   ==(omaduse 7 järgi)=(omaduse 6 järgi) =

   Asendage algses avaldises saadud näitajad. Saame:

   Vastus: 5.25

   Näide 2 Arvutage:

   

   Toome kõik logaritmid alusele 6 (sel juhul "migreeruvad" murdosa nimetaja logaritmid lugejasse):

   Jagame logaritmi märgi all olevad arvud algteguriteks:

   Rakenda atribuute 4 ja 6:

   Tutvustame asendust

   Saame:

   Vastus: 1

   Logaritm . Põhiline logaritmiline identiteet.

   Logaritmide omadused. Kümnendlogaritm. naturaallogaritm.

   logaritm positiivne arv N baasis (b > 0, b 1) nimetatakse eksponendiks x, milleni N saamiseks peate tõstma b .

   See kirje on samaväärne järgmisega: b x = N .

   NÄITED: log 3 81 = 4 kuna 3 4 = 81 ;

   log 1/3 27 = – 3, sest (1/3) - 3 = 3 3 = 27 .

   Ülaltoodud logaritmi definitsiooni saab kirjutada identiteedina:

   

   Logaritmide põhiomadused.

   2) log 1 = 0, sest b 0 = 1 .

   3) Korrutise logaritm võrdub tegurite logaritmide summaga:

   4) Jagatise logaritm võrdub dividendi ja jagaja logaritmide vahega:

   5) Kraadi logaritm võrdub eksponendi ja selle aluse logaritmi korrutisega:

   Selle omaduse tagajärjed on järgmised: palgijuur võrdub juurarvu logaritmiga, mis on jagatud juure astmega:

   

   6) Kui logaritmi alus on kraad, siis väärtus astendaja pöördväärtuse saab riimilogi märgist välja võtta:

   

   Kaks viimast omadust saab ühendada üheks:

   

   7) Üleminekumooduli valem (st üleminek logaritmi ühelt aluselt teisele):

   

   Konkreetsel juhul, kui N = a meil on:

   

   Kümnendlogaritm helistas baaslogaritm 10. Seda tähistatakse lg-ga, st. logi 10 N= log N. Arvude 10, 100, 1000, logaritmid. p on vastavalt 1, 2, 3, …, st. on nii palju positiivset

   ühikut, mitu nulli on logaritmarvus ühe järel. Arvude logaritmid 0,1, 0,01, 0,001, . p on vastavalt –1, –2, –3, …, st. on nii palju negatiivseid, kui on nullid logaritmi arvus enne ühte (sh null täisarvu). Ülejäänud arvude logaritmidel on murdosa, mida nimetatakse mantiss. Logaritmi täisarvulist osa nimetatakse iseloomulik. Praktilisteks rakendusteks on kõige mugavamad kümnendlogaritmid.

   naturaallogaritm helistas baaslogaritm e. Seda tähistatakse ln-ga, s.o. logi e N=ln N. Number e on irratsionaalne, selle ligikaudne väärtus on 2,718281828. See on piir, mille poole number (1 + 1 / n) n piiramatu suurenemisega n(cm. esimene imeline piir lehel Numbrijada piirangud).
   Nii kummaline kui see ka ei tundu, osutusid naturaallogaritmid väga mugavaks erinevate funktsioonide analüüsiga seotud toimingute tegemisel. Baaslogaritmide arvutamine e palju kiiremini kui mis tahes muul alusel.

• Mida on vaja täna Venemaal lapse adopteerimiseks? Lapsendamine Venemaal hõlmab lisaks vastutustundlikule isiklikule otsusele mitmeid kandidaatide riikliku kontrollimise protseduure. Jäik valik ettevalmistavas etapis aitab kaasa rohkem […]
• TIN-i või OGRN-i kaudu tasuta teave maksuregistrist kogu Venemaal - võrgus maksuteenuste ühtsel portaalil teave juriidiliste isikute, üksikettevõtjate riikliku registreerimise kohta, […]
• Karistus dokumentideta sõitmise eest (juhiluba, kindlustus, STS) Mõnikord istuvad juhid unustamise tõttu ilma lubadeta rooli ja saavad dokumentideta sõidu eest trahvi. Tuletage meelde, et autojuht, kes temaga veatult kaasa sõidab […]
• Lilled meestele. Milliseid lilli saab mehele kinkida? Milliseid lilli saab mehele kinkida? "Meeste" lilli pole nii palju, kuid on neid, mida kingitakse meestele. Väike nimekiri lilledest teie ees: krüsanteemid. Roosid. Nelgid. […]
• Memo on dokumendi erivorm, mida kasutatakse ettevõtte sisekeskkonnas ja mis aitab kiiresti lahendada jooksvaid tootmisprobleeme. Tavaliselt on see dokument koostatud eesmärgiga muuta […]
• Millal ja kuidas saada Sberbanki pensioni kogumisosa? Sberbank on riikliku pensionifondi partnerpank. Selle alusel said kogumispensioni väljastanud kodanikud kogumispensioni üle kanda kogumispensioni […]
• Lastetoetused Uljanovskis ja Uljanovski oblastis 2018. aastal Lisaks toimivad kõigis piirkondades föderaalseadusega kinnitatud programmid. Vaatame, kes ja milliste hüvede peale võib loota. Piirkondlike ametiasutustena […]
• Üksikasjaliku huvide kohtus esindamise volikirja koostamise üksikasjalik juhend Tsiviil- või vahekohtumenetluses, haldus- või kriminaalasjas võib nii hageja kui ka kostja huve esindada advokaat: […]

tuletatud selle määratlusest. Ja nii ka arvu logaritm b põhjusega a defineeritud kui astendaja, milleni arv tuleb tõsta a numbri saamiseks b(logaritm eksisteerib ainult positiivsete arvude puhul).

Sellest sõnastusest järeldub, et arvutus x=log a b, võrdub võrrandi lahendamisega kirves=b. Näiteks, log 2 8 = 3 sest 8 = 2 3 . Logaritmi sõnastus võimaldab põhjendada, et kui b=a c, siis arvu logaritm b põhjusega a võrdub Koos. Samuti on selge, et logaritmi teema on tihedalt seotud arvu astme teemaga.

Logaritmidega, nagu kõigi arvudega, saate sooritada liitmise, lahutamise tehted ja muuta igal võimalikul viisil. Kuid arvestades asjaolu, et logaritmid pole päris tavalised arvud, kehtivad siin omad erireeglid, mida nimetatakse põhiomadused.

Logaritmide liitmine ja lahutamine.

Võtke kaks logaritmi sama alusega: logi x ja logi a y. Pärast eemaldamist saate teha liitmise ja lahutamise toiminguid:

log a x+ log a y= log a (x y);

log a x - log a y = log a (x:y).

logi a(x 1 . x 2 . x 3 ... x k) = logi x 1 + logi x 2 + logi x 3 + ... + logi a x k.

Alates jagatislogaritmi teoreemid võib saada veel ühe logaritmi omaduse. On hästi teada, et logi a 1 = 0, seega

logi a 1 /b= log a 1 - palk a b= -log a b.

Seega on võrdsus:

log a 1 / b = - log a b.

Kahe vastastikku pöördarvu logaritmid samal alusel erinevad üksteisest ainult märgi poolest. Niisiis:

Log 3 9= - log 3 1/9 ; log 5 1 / 125 = -log 5 125.

274. Märkused.

a) Kui hinnatav avaldis sisaldab summa või erinevus arvud, siis tuleb need leida ilma tabelite abita tavalise liitmise või lahutamise teel. Näiteks:

log (35 + 7,24) 5 = 5 log (35 + 7,24) = 5 log 42,24.

b) Teades, kuidas avaldisi logaritmida, saame vastupidiselt antud logaritmi tulemusest leida avaldise, millest see tulemus saadi; nii et kui

logi X= log a+logi b- 3 palki Koos,

seda on lihtne ette kujutada

sisse) Enne logaritmitabelite struktuuri käsitlemist toome välja mõned kümnendlogaritmide omadused, s.t. need, milles on aluseks võetud arv 10 (arvutamiseks kasutatakse ainult selliseid logaritme).

Teine peatükk.

Kümnendlogaritmide omadused.

275 . a) Kuna 10 1 = 10, 10 2 = 100, 10 3 = 1000, 10 4 = 10 000 jne, siis log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4 jne.

Tähendab, nullidega ühega kujutatud täisarvu logaritm on positiivne täisarv, mis sisaldab nii palju ühelisi, kui arvu kujutisel on nulle.

Sellel viisil: log 100 000 = 5, logi 1000 000 = 6 , jne.

b) Sest

log 0,1 = -l; log 0,01 = -2; log 0,001 == -3; log 0,0001 = -4, jne.

Tähendab, kümnendmurru logaritm, mida kujutab ühik eesolevate nullidega, on negatiivne täisarv, mis sisaldab nii palju negatiivseid ühikuid, kui palju on murru kujutisel nulle, sealhulgas 0 täisarvu.

Sellel viisil: log 0,00001= -5, log 0,000001 = -6, jne.

sisse) Võtke näiteks täisarv, mida ei esinda nullidega ühik. 35 või täisarv murdosaga, nt. 10.7. Sellise arvu logaritm ei saa olla täisarv, kuna tõstes 10 täisarvulise astendajaga (positiivne või negatiivne) astmeni, saame 1 nullidega (1-le järgnev või eelnev). Oletame nüüd, et sellise arvu logaritm on mingi murdosa a / b . Siis oleks meil võrdsus

Kuid need võrdsused on võimatud, nagu 10a on 1 nullidega, samas kui astmed 35b ja 10,7b indikaatorit pole b ei saa anda 1 nullidega. Seetõttu ei saa seda lubada logi 35 ja logi 10.7 olid võrdsed murdosadega. Kuid logaritmifunktsiooni omaduste põhjal teame (), et igal positiivsel arvul on logaritm; Seetõttu on igal arvul 35 ja 10,7 oma logaritm ja kuna see ei saa olla täisarv ega murdarv, on see irratsionaalne arv ja seetõttu ei saa seda arvude abil täpselt väljendada. Tavaliselt väljendatakse irratsionaalseid logaritme ligikaudu kümnendmurruna mitme kümnendkohaga. Nimetatakse selle murru täisarvu (kuigi see oli "0 täisarvu"). iseloomulik, ja murdosa on logaritmi mantiss. Kui näiteks logaritm on 1,5441 , siis selle tunnus on 1 , ja mantiss on 0,5441 .

G) Võtame näiteks mõne täis- või segaarvu. 623 või 623,57 . Sellise arvu logaritm koosneb tunnusest ja mantissist. Selgub, et kümnendlogaritmidel on see mugavus leiame nende tunnuse alati ühe arvutüübi järgi . Selleks loendame, mitu numbrit on antud täisarvus või segaarvu täisarvus. Meie näidetes nende arvude kohta 3 . Seetõttu iga numbrit 623 ja 623,57 rohkem kui 100, kuid vähem kui 1000; mis tähendab, et igaühe logaritm on suurem logi 100, st rohkem 2 , aga vähem log 1000 st vähem 3 (pidage meeles, et suuremal arvul on ka suurem logaritm). Järelikult log 623 = 2,..., ja log 623,57 = 2,... (punktid asendavad tundmatuid mantissi).

Nii leiame:

10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,...

1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,...

Olgu üldiselt antud täisarv või antud segaarvu täisarv sisaldav osa m numbrid. Kuna väikseim täisarv sisaldab m numbrid, seal 1 Koos m - 1 lõpus nullid, siis (tähistab antud arvu N) saame kirjutada ebavõrdsed:

ja seega

m - 1 < log N < m ,

log N = ( m- 1) + positiivne murd.

Nii et omadus logN = m - 1 .

Sel viisil näeme seda täisarvu või segaarvu logaritmi tunnus sisaldab nii palju positiivseid kui arvu täisarvuosas on numbreid ilma üheta.

Seda silmas pidades võime otse kirjutada:

log 7205 = 0,...; log83 = 1,...; log 720,4 = 2,... jne.

e) Võtame mõned kümnendmurrud, mis on väiksemad kui 1 (st omades 0 täisarvud): 0,35; 0,07; 0,0056; 0,0008, jne.

Seega on kõik need logaritmid suletud kahe negatiivse täisarvu vahele, mis erinevad ühe võrra; nii et igaüks neist on võrdne neist negatiivsetest arvudest väiksemaga, mida on suurendatud mõne positiivse murdosa võrra. Näiteks, log0,0056= -3 + positiivne murd. Oletame, et see murd on 0,7482. Siis tähendab see:

log 0,0056 = - 3 + 0,7482 (= - 2,2518).

Summad nagu - 3 + 0,7482 , mis koosneb negatiivsest täisarvust ja positiivsest kümnendmurdust, nõustus kirjutama logaritmilistes arvutustes lühendatult järgmiselt: 3 ,7482 (Selline arv on järgmine: 3 miinusega, 7482 kümnetuhandik.), st nad panevad tunnuse kohale miinusmärgi, et näidata, et see viitab ainult sellele tunnusele, mitte aga mantissale, mis jääb positiivseks. Seega on ülaltoodud tabelist näha, et

log 0,35 == 1 ,....; log 0,07 = 2 ,....; log 0,0008 = 4 ,....

Lase üldse . on kümnendmurd, milles esimene oluline number α kulud m nullid, sealhulgas 0 täisarvu. Siis on selge, et

- m < log A < - (m- 1).

Kuna kahest täisarvust:- m ja - (m- 1) on väiksem m , siis

log A = - m+ positiivne murd,

ja seetõttu ka omadus log A = - m (positiivse mantissiga).

Sellel viisil, kümnendmurru, mis on väiksem kui 1, logaritmi karakteristik sisaldab sama palju negatiivseid, kui kümnendmurru kujutisel on nullid esimese tähendusliku numbri ees, sealhulgas null täisarvu; sellise logaritmi mantiss on positiivne.

e) Korrutage mõni arv N(tervik või murdosa – vahet pole) 10, 100 1000 võrra..., üldiselt nullidega 1 võrra. Vaatame, kuidas see muutub logi N. Kuna korrutise logaritm võrdub tegurite logaritmide summaga, siis

log(N 10) = log N + log 10 = log N + 1;

log(N 100) = log N + log 100 = log N + 2;

log(N 1000) = log N + log 1000 = log N + 3; jne.

Millal logi N lisame mõne täisarvu, siis saame selle arvu alati lisada tunnusele, mitte mantissile.

Seega, kui log N = 2,7804, siis 2,7804 + 1 = 3,7804; 2,7804 + 2 = 4,7801 jne;

või kui log N = 3,5649, siis 3,5649 + 1 = 2,5649; 3,5649 + 2 = 1,5649 jne.

Arvu korrutamisel 10, 100, 1000, .., tavaliselt nullidega 1-ga, logaritmi mantiss ei muutu ja tunnus suureneb nii mitme ühiku võrra, kui kordajas on nulle. .

Samamoodi, võttes arvesse, et jagatise logaritm on võrdne dividendi logaritmiga ilma jagaja logaritmita, saame:

log N / 10 = log N - log 10 = log N -1;

log N / 100 = log N - log 100 = log N -2;

log N / 1000 = log N - log 1000 = log N -3; jne.

Kui nõustume, et lahutame logaritmist täisarvu, lahutame selle täisarvu alati tunnusest ja jätame mantissi muutmata, siis võime öelda:

Arvu jagamisel 1-ga nullidega logaritmi mantiss ei muutu ja tunnus väheneb nii mitme ühiku võrra, kui jagajas on nulle.

276. Tagajärjed. Varalt ( e) saame järeldada järgmised kaks tagajärge:

a) Kümnendarvu logaritmi mantiss ei muutu arvus komaga nihutamisest , sest koma liigutamine võrdub korrutamise või jagamisega 10, 100, 1000 jne. Seega on arvude logaritmid:

0,00423, 0,0423, 4,23, 423

erinevad ainult omaduste poolest, kuid mitte mantisside poolest (eeldusel, et kõik mantissid on positiivsed).

b) Numbrite mantissid, millel on sama oluline osa, kuid erinevad lõpus ainult nullide võrra, on samad: seega, arvude logaritmid: 23, 230, 2300, 23 000 erinevad ainult tunnuste poolest.

Kommenteeri. Nendest kümnendlogaritmide omadustest on näha, et täisarvu ja kümnendmurru logaritmi karakteristiku leiame ilma tabelite abita (see on kümnendlogaritmide suur mugavus); selle tulemusena paigutatakse logaritmilistesse tabelitesse ainult üks mantiss; lisaks, kuna murdude logaritmide leidmine on taandatud täisarvude logaritmide leidmisele (murru logaritm \u003d lugeja logaritm ilma nimetaja logaritmita), paigutatakse ainult täisarvude logaritmide mantissid tabelid.

Kolmas peatükk.

Neljakohaliste tabelite seade ja kasutamine.

277. Logaritmisüsteemid. Logaritmide süsteem on logaritmide kogum, mis arvutatakse järjestikuste täisarvude jaoks samas baasis. Kasutatakse kahte süsteemi: tavaliste või kümnendlogaritmide süsteemi, mille aluseks on arv 10 , ja nn naturaallogaritmide süsteem, mille aluseks on irratsionaalarv (mõnedel põhjustel, mida mõistetakse teistes matemaatika harudes) 2,7182818 ... Arvutusteks kasutatakse kümnendlogaritme, mis tulenevad mugavustest, millele osutasime selliste logaritmide omaduste loetlemisel.

Naturaalseid logaritme nimetatakse logaritmide leiutaja, Šoti matemaatiku järgi ka Napieri logaritmideks. Nepera(1550–1617) ja kümnendlogaritmid – professori järgi nimetatud Briggi poolt brigga(Napieri kaasaegne ja sõber), kes koostas esmakordselt nende logaritmide tabelid.

278. Negatiivse logaritmi teisendamine positiivse mantissiga ja pöördteisendus. Oleme näinud, et 1-st väiksemate arvude logaritmid on negatiivsed. Seega koosnevad nad negatiivsest tunnusest ja negatiivsest mantissist. Selliseid logaritme saab alati teisendada nii, et nende mantiss on positiivne ja tunnus jääb negatiivseks. Selleks piisab, kui lisada mantissile positiivne ühik ja tunnusele negatiivne ühik (millest alates logaritmi väärtus muidugi ei muutu).

Kui meil on näiteks logaritm - 2,0873 , siis võid kirjutada:

- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,

või lühendatult:

Ja vastupidi, iga negatiivse karakteristiku ja positiivse mantissiga logaritmi saab muuta negatiivseks. Selleks piisab, kui kinnitada positiivsele mantissile negatiivne ühik ja negatiivsele omadusele positiivne: nii et võite kirjutada:

279. Neljakohaliste tabelite kirjeldus. Enamiku praktiliste ülesannete lahendamiseks piisab täiesti neljakohalistest tabelitest, mille käsitlemine on väga lihtne. Need tabelid (kirjaga "logaritmide" ülaosas) on paigutatud selle raamatu lõppu ja väike osa neist (asukoha selgitamiseks) on trükitud sellele lehele. Need sisaldavad mantissi

Logaritmid.

kõigi täisarvude logaritmid alates 1 enne 9999 kaasa arvatud, arvutatakse nelja kümnendkoha täpsusega, kusjuures viimast kümnendkohta suurendatakse võrra 1 kõigil juhtudel, kui 5. komakoht peab olema 5 või rohkem kui 5; seetõttu annavad 4-kohalised tabelid ligikaudsed mantissid kuni 1 / 2 kümnetuhandik osa (puudujäägi või ülejäägiga).

Kuna täisarvu või kümnendmurdu logaritmi saame otseselt iseloomustada, lähtudes kümnendlogaritmide omadustest, tuleb tabelitest võtta ainult mantiss; samas tuleb meeles pidada, et koma asukoht kümnendarvus, samuti nullide arv arvu lõpus, ei mõjuta mantissi väärtust. Seetõttu jätame antud arvule mantissi leidmisel kõrvale selles arvus oleva koma, samuti selle lõpus olevad nullid, kui neid on, ning leiame pärast seda moodustatud täisarvu mantissi. Sel juhul võivad tekkida järgmised juhtumid.

1) Täisarv koosneb 3 numbrist. Leiame näiteks arvu 536 logaritmi mantissi. Selle arvu kaks esimest numbrit ehk 53 asuvad tabelites esimeses vasakpoolses vertikaalses veerus (vt tabel). Olles leidnud numbri 53, liigume sellest mööda horisontaalset joont paremale, kuni see joon lõikub vertikaalse veeruga, mis läbib ühte ülaosas seatud numbritest 0, 1, 2, 3, ... 9 (ja tabeli alumine osa), mis tähistab selle arvu 3. numbrit, st meie näites arvu 6. Ristmikul saame mantissi 7292 (st 0,7292), mis kuulub arvu 536 logaritmi. numbrile 508 leiame mantissi 0,7059, numbrile 500 leiame 0,6990 jne.

2) Täisarv koosneb 2 või 1 numbrist. Seejärel omistame sellele arvule mõtteliselt üks või kaks nulli ja leiame nii moodustunud kolmekohalise arvu mantissi. Näiteks määrame arvule 51 ühe nulli, millest saame 510 ja leiame mantissi 7070; omistame numbrile 5 2 nulli ja leiame mantissi 6990 jne.

3) Täisarvu väljendatakse 4 numbriga. Näiteks peate leidma logi 5436 mantissi. Seejärel leiame tabelitest esmalt, nagu just märgitud, mantissi numbrile, mis on kujutatud selle numbri kolme esimese numbriga, st 543 jaoks (selleks mantissiks saab 7348 ); seejärel liigume leitud mantissist mööda horisontaaljoont paremale (tabeli paremale küljele, mis asub paksu püstjoone taga) kuni ristumiseni vertikaalse veeruga, mis läbib ühte numbritest: 1, 2 3, . .. 9, mis seisab selle tabeli osa ülaosas (ja allosas ), mis tähistab antud numbri 4. numbrit, st meie näites numbrit 6. Ristmikul leiame paranduse (number 5), mida tuleb mõttes rakendada mantissile 7348, et saada mantiss numbriga 5436; seega saame mantissiks 0,7353.

4) Täisarvu väljendatakse 5 või enama numbriga. Seejärel jätame kõik numbrid kõrvale, välja arvatud esimesed 4, ja võtame ligikaudse neljakohalise arvu ja suurendame selle numbri viimast numbrit 1 võrra. juhtum, kui arvu mahajäetud 5. number on 5 või rohkem kui 5. Seega võtame 57842 asemel 5784, 30257 asemel 3026, 583263 asemel 5833 jne. Selle ümardatud neljakohalise numbri jaoks leiame mantissi, nagu seda on nüüd selgitatud.

Nendest juhistest juhindudes leiame näiteks järgmiste arvude logaritmid:

36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.

Esiteks, praegu tabelitele viitamata, paneme kirja mõned omadused, jättes ruumi mantissidele, mille järel kirjutame:

log 36,5 = 1,... log 0,00345 = 3 ,....

log 804,7 = 2,... log 7,2634 = 0,....

log 0,26 = 1 ,... log 3456,86 = 3,....

log 36,5 = 1,5623; log 0,00345 = 3,5378;

log 804,7 = 2,9057; log 7,2634 = 0,8611;

log 0,26 = 1,4150; log 3456,86 = 3,5387.

280. Märkus. Mõnes neljakohalises tabelis (näiteks tabelites V. Lortšenko ja N. Ogloblin, S. Glazenap, N. Kamenštšikova) selle numbri 4. numbri parandusi ei tehta. Selliste tabelite käsitlemisel tuleb need parandused leida lihtsa arvutuse abil, mille saab teha järgmise tõe alusel: kui arvud on suuremad kui 100 ja nendevahelised erinevused on väiksemad kui 1, siis ilma sensitiivita viga võib eeldada, et logaritmide erinevused on võrdelised vastavate arvude erinevustega . Olgu näiteks vaja leida mantiss, mis vastab numbrile 5367. See mantiss on loomulikult sama, mis numbril 536,7. Tabelitest leiame mantissi 7292 arvu 536 jaoks. Võrreldes seda mantissiga 7300, mis asub paremal pool, mis vastab arvule 537, märkame, et kui arv 536 suureneb 1 võrra, siis tema mantiss suureneb 8 kümne võrra. -tuhandik (8 on nn tabeli erinevus kahe kõrvuti asetseva mantissi vahel); kui arv 536 suureneb 0,7 võrra, siis tema mantiss kasvab mitte 8 kümnetuhandiku võrra, vaid mõne väiksema arvu võrra X kümnetuhandik, mis lubatud proportsionaalsuse kohaselt peab vastama proportsioonile:

X :8=0,7:1; kus X = 8 07 = 5,6,

mis on ümardatud 6 kümnetuhandikuks. See tähendab, et numbri 536,7 (ja seega ka numbri 5367) mantiss on 7292 + 6 = 7298.

Pange tähele, et tabelites kahe kõrvuti asetseva arvu järgi vahearvu leidmist nimetatakse interpoleerimine. Siin kirjeldatud interpolatsiooni nimetatakse proportsionaalne, kuna see põhineb eeldusel, et logaritmi muutus on võrdeline arvu muutusega. Seda nimetatakse ka lineaarseks, kuna see eeldab, et graafiliselt väljendatakse logaritmilise funktsiooni muutust sirgjoonega.

281. Ligikaudse logaritmi veapiir. Kui arv, mille logaritmi otsitakse, on täpne arv, siis selle 4-kohalistes tabelites leiduva logaritmi veapiiri jaoks saame, nagu me juba ütlesime. 1 / 2 kümnetuhandik aktsia. Kui antud arv pole täpne, siis tuleb sellele veapiirile lisada ka teise vea piir, mis tuleneb arvu enda ebatäpsusest. On tõestatud (jätame selle tõendi välja), et sellise limiidi eest võib toodet võtta

a(d +1) kümme tuhandikku.,

kus a on kõige ebatäpsema arvu veapiir, eeldades, et Selle täisarvulises osas võetakse 3 numbrit, a d mantisside tabeli erinevus, mis vastab kahele järjestikusele kolmekohalisele numbrile, mille vahel on see ebatäpne arv. Seega väljendatakse logaritmi lõppvea piir järgmise valemiga:

1 / 2 + a(d +1) kümnetuhandik

Näide. Leia logi π , võttes π ligikaudne arv 3,14, täpne 1 / 2 sajandik.

Liigutades arvus 3.14 koma pärast 3. numbrit, vasakult lugedes saame kolmekohalise arvu 314, täpselt kuni 1 / 2 ühikud; see tähendab, et ebatäpse arvu veapiir, st see, mida tähistasime tähega a , kui 1 / 2 Tabelitest leiame:

log 3,14 = 0,4969.

Tabeli erinevus d arvude 314 ja 315 mantisside vahel on 14, seega on leitud logaritmi viga väiksem

1 / 2 + 1 / 2 (14 +1) = 8 kümnetuhandik.

Kuna me ei tea 0,4969 logaritmi kohta, kas see on alla või üle, saame tagada ainult täpse logaritmi π on vahemikus 0,4969–0,0008 ja 0,4969 + 0,0008, st 0,4961< log π < 0,4977.

282. Leia antud logaritmi järgi arv. Arvu leidmiseks etteantud logaritmi järgi saab kasutada samu tabeleid, mille järgi leitakse nende arvude mantissid; aga mugavam on kasutada muid tabeleid, kuhu on paigutatud nn antilogaritmid ehk antud mantissidele vastavad numbrid. Need tabelid, mille ülaosas on silt "antilogaritmid", on paigutatud selle raamatu lõppu, järgides logaritmide tabeleid; väike osa neist on paigutatud sellele lehele (selgitamiseks).

Olgu antud 4-kohaline mantiss 2863 (tunnusele ei pööra tähelepanu) ja selleks on vaja leida vastav täisarv. Seejärel, omades antilogaritmide tabeleid, peame neid kasutama täpselt samamoodi, nagu eelnevalt selgitati antud numbri mantissi leidmisel, nimelt: esimesest vasakpoolsest veerust leiame mantissi 2 esimest numbrit. Seejärel liigume nendelt numbritelt mööda horisontaaljoont paremale kuni ristumiseni vertikaalse veeruga, mis tuleb mantissi 3. numbrist, mida tuleb otsida ülemiselt (või alumiselt) realt. Ristmikul leiame neljakohalise numbri 1932, mis vastab mantissile 286. Seejärel liigume sellelt numbrilt edasi mööda horisontaaljoont paremale kuni ristumiseni mantissi 4. numbrilt tuleva vertikaalsambaga, mis peab leida ülevalt (või alumiselt) numbrite 1, 2 hulgast panna sinna , 3,... 9. Ristmikult leiame paranduse 1, mida tuleb (mõttes) rakendada varem leitud arvule 1032 et saada mantissile 2863 vastav arv.

Seega saab numbriks 1933. Pärast seda tunnusele tähelepanu pöörates tuleb numbrisse 1933 panna hõivatu õigele kohale. Näiteks:

kui logi x = 3,2863, siis X = 1933,

„ logi x= 1,2863, „ X = 19,33,

, logi x = 0,2&63, „ X = 1,933,

„ logi x = 2 ,2863, „ X = 0,01933

Siin on veel näiteid:

logi x = 0,2287, X = 1,693,

logi x = 1 ,7635, X = 0,5801,

logi x = 3,5029, X = 3184,

logi x = 2 ,0436, X = 0,01106.

Kui mantiss sisaldab 5 või enam numbrit, siis võtame ainult esimesed 4 numbrit, jättes ülejäänud kõrvale (ja suurendame neljandat numbrit 1 võrra, kui 5. number on viis või rohkem). Näiteks mantissa 35478 asemel võtame 3548, 47562 asemel 4756.

283. Märkus. Mantissi 4. ja järgmise numbri paranduse saab leida ka interpoleerimise teel. Seega, kui mantiss on 84357, siis, leides mantissile 843 vastava arvu 6966, saame edasi mõelda järgmiselt: kui mantiss suureneb 1 (tuhandik) võrra, s.o on tehtud 844, siis on see arv, nagu tabelitest näha, suureneb 16 ühiku võrra; kui mantiss ei suurene mitte 1 (tuhandik) võrra, vaid 0,57 (tuhandik) võrra, siis see arv suureneb X ühikut ja X peaks vastama proportsioonidele:

X : 16 = 0,57: 1, kust x = 16 0,57 = 9,12.

See tähendab, et soovitud arv on 6966 + 9,12 = 6975,12 või (ainult neljakohaline) 6975.

284. Leitud numbri veapiir. On tõestatud, et juhul, kui leitud arvus on koma pärast 3. numbrit vasakult, st kui logaritmi tunnus on 2, võib veapiiriks võtta summa

kus a on selle logaritmi veapiir (väljendatuna kümnetuhandikes), mille abil arv leiti, ja d - kahe kolmekohalise järjestikuse numbri mantisside vahe, mille vahele jääb leitud number (komaga pärast 3. numbrit vasakult). Kui tunnus pole mitte 2, vaid mõni muu, siis tuleb leitud arvus koma vasakule või paremale nihutada, st jagada või korrutada arv teatud astmega 10. Sel juhul on viga tulemus jagatakse või korrutatakse sama astmega 10.

Leiame näiteks arvu logaritmi järgi 1,5950 , mille täpsus on teadaolevalt 3 kümnetuhandik; nii siis a = 3 . Sellele logaritmile vastav arv, mis on leitud antilogaritmide tabelist, on 39,36 . Kui liigutate koma pärast 3. numbrit vasakul, saame numbri 393,6 vahel 393 ja 394 . Logaritmi tabelitest näeme, et nendele kahele arvule vastavate mantisside vahe on 11 kümnetuhandik; tähendab d = 11 . Numbri 393,6 viga on väiksem

Nii et numbri viga 39,36 jääb vähemaks 0,05 .

285. Toimingud negatiivsete tunnustega logaritmidele. Logaritmide liitmine ja lahutamine ei tekita raskusi, nagu on näha järgmistest näidetest:

Samuti pole raskusi logaritmi positiivse arvuga korrutamisel, näiteks:

Viimases näites korrutatakse positiivne mantiss eraldi 34-ga, seejärel korrutatakse negatiivne tunnus 34-ga.

Kui negatiivse tunnuse ja positiivse mantissi logaritm korrutada negatiivse arvuga, siis toimivad need kahel viisil: kas eelnevalt antud logaritm muudetakse negatiivseks või korrutatakse mantiss ja tunnus eraldi ning tulemused liidetakse kokku, näide:

3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;

3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.

Jagamisel on kaks juhtumit: 1) negatiivne tunnus on jagatud ja 2) ei jagu jagajaga. Esimesel juhul eraldatakse tunnus ja mantiss eraldi:

10 ,3784: 5 = 2 ,0757.

Teisel juhul lisatakse tunnusele nii palju negatiivseid ühikuid, et saadud arv jagub jagajaga; mantissile lisatakse sama arv positiivseid ühikuid:

3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.

See teisendus tuleb teha meeles, nii et toiming on korraldatud järgmiselt:

286. Lahutatud logaritmide asendamine terminitega. Mõnda keerukat avaldist logaritmide abil arvutades tuleb mõned logaritmid liita, teised lahutada; sel juhul leiavad nad tavapärasel toimingute sooritamisel eraldi logaritmide liikmete summa, seejärel lahutatute summa ja lahutavad esimesest summast teise. Näiteks kui meil on:

logi X = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,

siis tavapärane toimingute täitmine paikneb järgmiselt:

Lahutamist on aga võimalik asendada liitmisega. Niisiis:

Nüüd saate arvutuse korraldada järgmiselt:

287. Arvutuste näited.

Näide 1. Hinda väljendit:

kui A = 0,8216, B = 0,04826, C = 0,005127 ja D = 7,246.

Logaritme selle avaldise:

logi X= 1/3 log A + 4 log B - 3 log C - 1/3 log D

Nüüd, et vältida tarbetut ajakaotust ja vähendada vigade võimalust, korraldame kõigepealt kõik arvutused ilma neid veel teostamata ja seega tabelitele viitamata:

Pärast seda võtame tabelid ja paneme vasakpoolsetesse tühjadesse kohtadesse logaritmid:

Vea piir. Kõigepealt leiame numbri vealimiidi x 1 = 194,5 võrdne:

Nii et kõigepealt peate leidma a , st ligikaudse logaritmi veapiir, väljendatuna kümnetuhandikes. Oletame, et need numbrid A, B, C ja D kõik on täpsed. Siis on üksikute logaritmide vead järgmised (kümnetuhandikes):

sisse logA.......... 1 / 2

sisse 1/3 log A......... 1 / 6 + 1 / 2 = 2 / 3

( 1 / 2 lisatud, kuna jagades 3 logaritmiga 1,9146, ümardasime jagatise, jättes kõrvale selle 5. numbri ja seetõttu tegime veel ühe vea, vähem 1 / 2 kümnetuhandik).

Nüüd leiame logaritmi veapiiri:

a = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (kümme tuhandikku).

Defineerime täpsemalt d . Sest x 1 = 194,5 , siis 2 järjestikust täisarvu, mille vahel on x 1 tahe 194 ja 195 . Tabeli erinevus d nendele numbritele vastavate mantisside vahel on võrdne 22 . Seega numbri veapiir x 1 seal on:

Sest x = x 1 : 10, siis arvu veapiir x võrdub 0,3:10 = 0,03 . Seega number, mille me leidsime 19,45 erineb täpsest arvust vähem kui 0,03 . Kuna me ei tea, kas meie lähenduses on leitud puudujääk või liig, saame vaid garanteerida, et

19,45 + 0,03 > X > 19,45 - 0,03 , st.

19,48 > X > 19,42 ,

ja seetõttu, kui me nõustume X =19,4 , siis on meil ligikaudne miinus kuni 0,1.

Näide 2 Arvutama:

X = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .

Kuna negatiivsetel arvudel pole logaritme, leiame kõigepealt:

X" = (2,31) 3 5 √72

lagunemise teel:

logi X"= 3 log 2,31 + 1/5 log72.

Pärast arvutust on järgmine:

X" = 28,99 ;

Järelikult

x = - 28,99 .

Näide 3. Arvutama:

Pidevat logaritmi siin rakendada ei saa, kuna juuremärgi all seisab y m m a. Sellistel juhtudel arvutatakse valem osadena.

Kõigepealt leiame N = 5 √8 , pärast N 1 = 4 √3 ; Seejärel määrame lihtsa liitmise teel N+ N 1 ja lõpuks arvutada 3 √N+ N 1 ; selgub:

N = 1,514, N 1 = 1,316 ; N+ N 1 = 2,830 .

logi x= log 3 √ 2,830 = 1 / 3 logi 2 830 = 0,1506 ;

x = 1,415 .

Neljas peatükk.

Eksponent- ja logaritmvõrrandid.

288. Eksponentvõrrand on selline, mille eksponendisse on kaasatud tundmatu ja logaritmiline- need, millesse märgi alla siseneb tundmatu logi. Selliseid võrrandeid saab lahendada ainult erijuhtudel ja lähtuda tuleb logaritmide omadustest ja põhimõttest, et kui arvud on võrdsed, siis on nende logaritmid võrdsed ja vastupidi, kui logaritmid on võrdsed, siis vastavad numbrid on võrdsed.

Näide 1 Lahendage võrrand: 2 x = 1024 .

Logaritme võrrandi mõlemad pooled:

Näide 2 Lahendage võrrand: a 2x - a x = 1 . Panek a x = juures , saame ruutvõrrandi:

y 2 - juures - 1 = 0 ,

Sest 1-√5 < 0 , siis on viimane võrrand võimatu (funktsioon a x alati on positiivne arv) ja esimene annab:

Näide 3 Lahendage võrrand:

log( a + x) + log ( b + x) = log ( c + x) .

Võrrandi saab kirjutada järgmiselt:

logi[( a + x) (b + x)] = logi ( c + x) .

Logaritmide võrdsusest järeldame arvude võrdsuse kohta:

(a + x) (b + x) = c + x .

See on ruutvõrrand, mille lahendamine pole keeruline.

Viies peatükk.

Liitintressid, tähtajalised maksed ja kiirmaksed.

289. Liitintressi põhiprobleem. Mis on kapitali suurus a rubla, antud kasvu poolt R liitintress pärast t aastat ( t on täisarv)?

Väidetavalt antakse kapital liitintressiga, kui arvestada nn "intressi intressiga" ehk siis, kui iga aasta lõpus lisatakse kapitalile tasumisele kuuluv intressiraha kapitalile, et suurendage seda järgmistel aastatel huviga.

Iga üle antud kapitali rubla R %, toob ühe aasta jooksul kasumit lk / 100 rubla ja järelikult muutub iga kapitali rubla 1 aasta jooksul 1 + lk / 100 rubla (näiteks kui kapital on antud 5 %, siis muutub iga rubla aastas 1 + 5 / 100 , st sisse 1,05 rubla).

Tähistab lühiduse huvides murdosa lk / 100 üks täht näiteks r , võime öelda, et iga kapitali rubla aastas muutub 1 + r rublad; Järelikult a rublad muutuvad 1 aastaga a (1 + r ) hõõruda. Aasta hiljem, s.o 2 aastat pärast kasvu algust, iga rubla nendest a (1 + r ) hõõruda. pöördub tagasi 1 + r hõõruda.; See tähendab, et kogu kapital konverteeritakse a (1 + r ) 2 hõõruda. Samamoodi leiame, et kolme aasta pärast on pealinn a (1 + r ) 3 , on nelja aasta pärast a (1 + r ) 4 ,... üldiselt läbi t aastat, kui t on täisarv, muutub see arvuks a (1 + r ) t hõõruda. Seega, tähistades AGA lõplik kapital, on meil järgmine liitintressivalem:

AGA = a (1 + r ) t kus r = lk / 100 .

Näide. Lase a =2300 rubla, lk = 4, t=20 aastat; siis valem annab:

r = 4 / 100 = 0,04 ; A = 2300 (1,04) 20.

Arvutada AGA, kasutame logaritme:

logi a = log 2 300 + 20 log 1,04 = 3,3617 + 20 0,0170 = 3,3617 + 0,3400 = 3,7017.

A=5031 rubla.

Kommenteeri. Selles näites oli meil logi 1.04 korrutada 20 . Alates numbrist 0,0170 on ligikaudne logi 1.04 kuni 1 / 2 kümnetuhandik osa, siis selle arvu korrutis 20 jääb ainult kuni 1 / 2 20, st kuni 10 kümnetuhandik \u003d 1 tuhandik. Seega kokku 3,7017 me ei saa garanteerida mitte ainult kümnetuhandike arvu, vaid ka tuhandendike arvu eest. Sellistel juhtudel suurema täpsuse saavutamiseks on see numbri jaoks parem 1 + r võta logaritmid mitte 4-kohalised, vaid näiteks suure arvu numbritega. 7 numbrit. Selleks esitame siin väikese tabeli, milles on kõige levinumate väärtuste jaoks välja kirjutatud 7-kohalised logaritmid. R .

290. Kiirmaksete põhiülesanne. Keegi võttis a rubla eest R % tingimusega tasuda võlg koos sellelt tasumisele kuuluvate intressidega sisse t aastat, makstes iga aasta lõpus sama summa. Mis see summa peaks olema?

Summa x Sellistel tingimustel igal aastal makstud makset nimetatakse kiirmakseks. Tähistame uuesti r aasta intressi raha alates 1 rubla, see tähendab, et number lk / 100 . Siis esimese aasta lõpuks võlg a tõuseb kuni a (1 + r ), pärast maksmist X rubla see tehakse ära a (1 + r )-X .

Teise aasta lõpuks muutub iga selle summa rubla uuesti ümber 1 + r rubla ja seetõttu jääb võlg [ a (1 + r )-X ](1 + r ) = a (1 + r ) 2 - x (1 + r ) ja tasu eest x rublad on: a (1 + r ) 2 - x (1 + r ) - X . Samamoodi hoolitseme selle eest, et 3. aasta lõpuks oleks võlg

a (1 + r ) 3 - x (1 + r ) 2 - x (1 + r ) - x ,

ja üldiselt ja lõpp t -ndal aastal on see:

a (1 + r ) t - x (1 + r ) t-1 - x (1 + r ) t-2 ... - x (1 + r ) - x , või

a (1 + r ) t - x [ 1 + (1 + r ) + (1 + r ) 2 + ...+ (1 + r ) t-2 + (1 + r ) t-1 ]

Sulgudes olev polünoom esindab geomeetrilise progressiooni liikmete summat; millel on esimene liige 1 , viimane ( 1 + r ) t-1 ja nimetaja ( 1 + r ). Geomeetrilise progressiooni liikmete summa valemi järgi (§ 10 ptk 3 § 249) leiame:

ja võlasumma pärast t - makse on:

Vastavalt ülesandele võlg lõpus t -th aasta peaks olema võrdne 0 ; sellepärast:

kus

Selle arvutamisel kiirmakse valemid logaritme kasutades peame esmalt leidma abiarvu N = (1 + r ) t logaritmi järgi: logN= t log (1 + r) ; leidmine N, lahutage sellest 1, siis saame valemi nimetaja X, mille järel sekundaarse logaritmi abil leiame:

logi X= log a+ log N + log r - log (N - 1).

291. Kiireloomuliste kaastööde põhiülesanne. Iga aasta alguses kannab keegi panka sama summa a hõõruda. Tehke kindlaks, milline kapital pärast nendest sissemaksetest moodustub t aastat, kui pank maksab R liitintress.

Märgistades läbi r aasta intressiraha alates 1 rubla, s.o. lk / 100 , vaidleme nii: esimese aasta lõpuks pealinna a (1 + r );

2. aasta alguses see summa lisandub a rublad; See tähendab, et sel ajal on pealinnas a (1 + r ) + a . 2. aasta lõpuks teeb ta seda a (1 + r ) 2 + a (1 + r );

3. aasta alguses võetakse uuesti kasutusele a rublad; See tähendab, et sel ajal on pealinnas a (1 + r ) 2 + a (1 + r ) + a ; 3. lõpuks saab ta olema a (1 + r ) 3 + a (1 + r ) 2 + a (1 + r ) Neid kaalutlusi edasi jätkates leiame, et lõpuks t aastal nõutud kapitali A saab:

See on iga aasta alguses tehtavate tähtajaliste sissemaksete valem.

Sama valemi võib saada järgmise arutluskäiguga: esimene sissemakse sisse a rubla pangas olles t aastat, muutub liitintressi valemi järgi sisse a (1 + r ) t hõõruda. Teine osamakse, olles pangas aasta vähem, s.o. t - 1 aastat, kontakt a (1 + r ) t-1 hõõruda. Samamoodi annab kolmas osamakse a (1 + r ) t-2 jne ja lõpuks pöördub viimane osamakse, olles pangas vaid 1 aasta a (1 + r ) hõõruda. Seega viimane pealinn A hõõruda. saab:

A= a (1 + r ) t + a (1 + r ) t-1 + a (1 + r ) t-2 + . . . + a (1 + r ),

mis pärast lihtsustamist annab ülaltoodud valemi.

Selle valemi logaritmide abil arvutamisel peate tegema sama, mis kiirmaksete valemi arvutamisel, st kõigepealt leidke arv N = ( 1 + r ) t selle logaritmi järgi: logN= t logi(1 + r ), seejärel number N-1 ja seejärel võtke valemi logaritm:

log A = palk a+log(1+ r) + log (N - 1) - 1ogr

Kommenteeri. Kui kiireloomuline panus a hõõruda. ei tehtud mitte alguses, vaid iga aasta lõpus (nagu näiteks tehakse kiirmakse X võlg tagasi maksta), siis nagu eelminegi vaieldes leiame, et lõpuks t aastal nõutud kapitali AGA" hõõruda. saab (kaasa arvatud viimane osamakse a hõõruda, ei kanna intressi):

A"= a (1 + r ) t-1 + a (1 + r ) t-2 + . . . + a (1 + r ) + a

mis on võrdne:

st. AGA" ilmub ( 1 + r ) korda vähem AGA, mida oli oodata, kuna iga rubla kapitali AGA" lebab pangas aasta vähem kui vastav kapitali rubla AGA.