Si të gjeni një vektor matricë. Ekuacioni karakteristik i një matrice

Një vektor vetjak i një matrice katrore është ai që, kur shumëzohet me një matricë të caktuar, rezulton në një vektor kolinear. Me fjalë të thjeshta, kur shumëzojmë një matricë me një vektor eigen, ky i fundit mbetet i njëjtë, por i shumëzuar me një numër të caktuar.

Përkufizimi

Një vektor vetjak është një vektor V jo zero, i cili, kur shumëzohet me një matricë katrore M, bëhet vetë i rritur me një numër λ. Në shënimin algjebrik duket kështu:

M × V = λ × V,

ku λ është eigenvlera e matricës M.

Le të shohim një shembull numerik. Për lehtësinë e regjistrimit, numrat në matricë do të ndahen me një pikëpresje. Le të kemi një matricë:

• M = 0; 4;
• 6; 10.

Le ta shumëzojmë atë me një vektor kolone:

• V = -2;

Kur shumëzojmë një matricë me një vektor kolone, marrim gjithashtu një vektor kolone. E rreptë gjuha matematikore formula për shumëzimin e një matrice 2 × 2 me një vektor kolone do të duket si kjo:

• M × V = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21.

M11 nënkupton elementin e matricës M që ndodhet në rreshtin e parë dhe kolonën e parë, dhe M22 nënkupton elementin e vendosur në rreshtin e dytë dhe kolonën e dytë. Për matricën tonë, këta elementë janë të barabartë me M11 = 0, M12 = 4, M21 = 6, M22 10. Për një vektor kolone, këto vlera janë të barabarta me V11 = –2, V21 = 1. Sipas kësaj formule, marrim rezultati i radhës produkti i një matrice katrore dhe një vektori:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Për lehtësi, le të shkruajmë vektorin e kolonës në një rresht. Pra, ne shumëzuam matricën katrore me vektorin (-2; 1), duke rezultuar në vektorin (4; -2). Natyrisht, ky është i njëjti vektor i shumëzuar me λ = -2. Lambda në këtë rast tregon vlerën e vet të matricës.

Vektori i një matrice është një vektor kolinear, domethënë një objekt që nuk ndryshon pozicionin e tij në hapësirë ​​kur shumëzohet me një matricë. Koncepti i kolinearitetit në algjebër vektoriale është i ngjashëm me termin e paralelizmit në gjeometri. Në interpretimin gjeometrik, vektorët kolinearë janë segmente të drejtuara paralele gjatësi të ndryshme. Që nga koha e Euklidit, ne e dimë se një drejtëz ka një numër të pafund të drejtëzave paralele me të, kështu që është logjike të supozojmë se çdo matricë ka një numër të pafund eigjenvektorësh.

Nga shembulli i mëparshëm është e qartë se vetvektorët mund të jenë (-8; 4), dhe (16; -8), dhe (32, -16). Këta janë të gjithë vektorë kolinearë që korrespondojnë me vlerën vetjake λ = -2. Kur shumëzojmë matricën origjinale me këta vektorë, përsëri do të përfundojmë me një vektor që ndryshon nga origjinali me 2 herë. Kjo është arsyeja pse, kur zgjidhen problemet e gjetjes së një vektori të veçantë, është e nevojshme të gjesh vetëm objekte vektoriale të pavarura lineare. Më shpesh, për një matricë n × n, ka një numër n eigenvektorësh. Llogaritësi ynë është krijuar për analizën e matricave katrore të rendit të dytë, kështu që pothuajse gjithmonë rezultati do të gjejë dy vektorë vetjakë, përveç rasteve kur ato përkojnë.

Në shembullin e mësipërm, ne e dinim paraprakisht eigenvektorin e matricës origjinale dhe përcaktuam qartë numrin lambda. Sidoqoftë, në praktikë, gjithçka ndodh anasjelltas: së pari gjenden eigenvlerat dhe vetëm më pas eigenvektorët.

Algoritmi i zgjidhjes

Le të shohim përsëri matricën origjinale M dhe të përpiqemi të gjejmë të dy eigenvektorët e saj. Pra, matrica duket si kjo:

• M = 0; 4;
• 6; 10.

Fillimisht duhet të përcaktojmë vlerën e vet λ, e cila kërkon llogaritjen e përcaktorit të matricës së mëposhtme:

• (0 − λ); 4;
• 6; (10 − λ).

Kjo matricë fitohet duke zbritur të panjohurën λ nga elementet në diagonalen kryesore. Përcaktori përcaktohet duke përdorur formulën standarde:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Meqenëse vektori ynë duhet të jetë jo zero, ne e pranojmë ekuacionin që rezulton si i varur linearisht dhe e barazojmë përcaktuesin tonë detA me zero.

(0 − λ) × (10 − λ) − 24 = 0

Le të hapim kllapat dhe të marrim ekuacionin karakteristik të matricës:

λ 2 − 10λ − 24 = 0

Kjo është standarde ekuacioni kuadratik, e cila duhet të zgjidhet përmes diskriminuesit.

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

Rrënja e diskriminuesit është sqrt(D) = 14, pra λ1 = -2, λ2 = 12. Tani për çdo vlerë lambda duhet të gjejmë vektorin e vet. Le të shprehim koeficientët e sistemit për λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

Në këtë formulë, E është matrica e identitetit. Bazuar në matricën që rezulton, ne krijojmë një sistem ekuacionet lineare:

2x + 4y = 6x + 12y,

ku x dhe y janë elementët vetvektorë.

Le të mbledhim të gjitha X-të në të majtë dhe të gjitha Y-të në të djathtë. Natyrisht - 4x = 8y. Ndani shprehjen me - 4 dhe merrni x = –2y. Tani mund të përcaktojmë vetvektorin e parë të matricës, duke marrë çdo vlerë të të panjohurave (kujtoni pafundësinë e eigjenvektorëve të varur linearisht). Le të marrim y = 1, pastaj x = –2. Prandaj, vetvektori i parë duket si V1 = (–2; 1). Kthehuni në fillim të artikullit. Ishte ky objekt vektori me të cilin ne shumëzuam matricën për të demonstruar konceptin e një vektori vetjak.

Tani le të gjejmë vetvektorin për λ = 12.

• M - λ × E = -12; 4
• 6; -2.

Le të krijojmë të njëjtin sistem ekuacionesh lineare;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x = y.

Tani marrim x = 1, pra y = 3. Kështu, eigenvektori i dytë duket si V2 = (1; 3). Kur shumëzohet matrica origjinale me një vektor të caktuar, rezultati do të jetë gjithmonë i njëjti vektor shumëzuar me 12. Këtu përfundon algoritmi i zgjidhjes. Tani ju e dini se si të përcaktoni manualisht eigenvektorin e një matrice.

• përcaktues;
• gjurma, domethënë shuma e elementeve në diagonalen kryesore;
• rang, domethënë numri maksimal i rreshtave/kolonave linearisht të pavarura.

Programi funksionon sipas algoritmit të mësipërm, duke shkurtuar sa më shumë procesin e zgjidhjes. Është e rëndësishme të theksohet se në program lambda përcaktohet me shkronjën "c". Le të shohim një shembull numerik.

Shembull se si funksionon programi

Le të përpiqemi të përcaktojmë eigenvektorët për matricën e mëposhtme:

• M = 5; 13;
• 4; 14.

Le t'i fusim këto vlera në qelizat e kalkulatorit dhe të marrim përgjigjen në formën e mëposhtme:

• Rangu i matricës: 2;
• Përcaktori i matricës: 18;
• Gjurmë matrice: 19;
• Llogaritja e eigjenvektorit: c 2 − 19.00c + 18.00 (ekuacion karakteristik);
• Llogaritja e eigenvektorit: 18 (vlera e parë lambda);
• Llogaritja e eigenvektorit: 1 (vlera e dytë lambda);
• Sistemi i ekuacioneve për vektorin 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistemi i ekuacioneve për vektorin 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vektori vetjak 1: (1; 1);
• Vektori vetjak 2: (-3,25; 1).

Kështu, kemi marrë dy eigenvektorë të pavarur linearisht.

konkluzioni

Algjebra lineare dhe gjeometria analitike janë lëndë standarde për çdo student fillestar të inxhinierisë. Nje numer i madh i vektorët dhe matricat janë të frikshëm, dhe në llogaritje të tilla të rënda është e lehtë të bësh gabime. Programi ynë do t'i lejojë studentët të kontrollojnë llogaritjet e tyre ose të zgjidhin automatikisht problemin e gjetjes së një vektori vetjak. Në katalogun tonë ka kalkulatorë të tjerë të algjebrës, i përdorni ato në studimet ose punën tuaj.

Matricat diagonale kanë strukturën më të thjeshtë. Shtrohet pyetja nëse është e mundur të gjendet një bazë në të cilën matrica e operatorit linear do të kishte një formë diagonale. Një bazë e tillë ekziston.
Le të na jepet një hapësirë ​​lineare R n dhe një operator linear A që vepron në të; në këtë rast, operatori A merr R n në vetvete, domethënë A:R n → R n .

Përkufizimi. Një vektor jozero quhet eigenvektor i operatorit A nëse operatori A përkthehet në një vektor kolinear, domethënë. Numri λ quhet eigenvalue ose eigenvalue i operatorit A, që i korrespondon eigenvektorit.
Le të vëmë re disa veti të eigenvlerave dhe eigenvektorëve.
1. Çdo kombinim linear i vetvektorëve Operatori A që i korrespondon të njëjtës eigenvale λ është një vektor eigen me të njëjtën vlerë eigen.
2. Eigenvektorët operatori A me vlera eigjene të ndryshme në çift λ 1 , λ 2 , ..., λ m janë linearisht të pavarur.
3. Nëse vlerat vetjake λ 1 =λ 2 = λ m = λ, atëherë vlera vetjake λ korrespondon me jo më shumë se m eigenvektorë të pavarur linearisht.

Pra, nëse ka n eigjenvektorë të pavarur linearisht , që korrespondojnë me vlera të ndryshme eigen λ 1, λ 2, ..., λ n, atëherë ato janë linearisht të pavarura, prandaj mund të merren si bazë e hapësirës R n. Le të gjejmë formën e matricës së operatorit linear A në bazë të vetvektorëve të tij, për të cilin do të veprojmë me operatorin A në bazë të vektorëve: Pastaj .
Kështu, matrica e operatorit linear A në bazë të eigenvektorëve të tij ka një formë diagonale, dhe vlerat vetjake të operatorit A janë përgjatë diagonales.
A ka një bazë tjetër në të cilën matrica ka një formë diagonale? Përgjigja për këtë pyetje jepet nga teorema e mëposhtme.

Teorema. Matrica e një operatori linear A në bazën (i = 1..n) ka një formë diagonale nëse dhe vetëm nëse të gjithë vektorët e bazës janë eigjenvektorë të operatorit A.

Rregulla për gjetjen e vlerave vetjake dhe eigenvektorëve

Le të jepet një vektor , ku x 1, x 2, ..., x n janë koordinatat e vektorit në lidhje me bazën dhe është eigenvektori i operatorit linear A që korrespondon me vlerën e vet λ, domethënë. Kjo marrëdhënie mund të shkruhet në formë matrice

. (*)

Ekuacioni (*) mund të konsiderohet si një ekuacion për gjetjen e , dhe, domethënë, ne jemi të interesuar për zgjidhje jo të parëndësishme, pasi vetvektori nuk mund të jetë zero. Dihet se zgjidhjet jotriviale të një sistemi homogjen ekuacionesh lineare ekzistojnë nëse dhe vetëm nëse det(A - λE) = 0. Pra, që λ të jetë një vlerë e veçantë e operatorit A është e nevojshme dhe e mjaftueshme që det(A - λE) ) = 0.
Nëse ekuacioni (*) shkruhet në mënyrë të detajuar në formë koordinative, atëherë marrim një sistem linear ekuacionet homogjene:

(1)
Ku - matrica e operatorit linear.

Sistemi (1) ka një zgjidhje jo zero nëse përcaktorja e tij D është e barabartë me zero

Ne morëm një ekuacion për gjetjen e vlerave vetjake.
Ky ekuacion quhet ekuacion karakteristik dhe i tij ana e majte- polinomi karakteristik i matricës (operatori) A. Nëse polinomi karakteristik nuk ka rrënjë reale, atëherë matrica A nuk ka vetvektorë dhe nuk mund të reduktohet në formë diagonale.
Le të jenë λ 1, λ 2, …, λ n rrënjët reale të ekuacionit karakteristik dhe midis tyre mund të ketë shumëfisha. Duke i zëvendësuar këto vlera në sistemin (1), gjejmë eigenvektorët.

Shembulli 12. Operatori linear A vepron në R 3 sipas ligjit, ku x 1, x 2, .., x n janë koordinatat e vektorit në bazë , , . Gjeni eigenvlerat dhe eigenvektorët e këtij operatori.
Zgjidhje. Ne ndërtojmë matricën e këtij operatori:
.
Ne krijojmë një sistem për përcaktimin e koordinatave të eigenvektorëve:

Ne hartojmë një ekuacion karakteristik dhe e zgjidhim atë:

.
λ 1,2 = -1, λ 3 = 3.
Duke zëvendësuar λ = -1 në sistem, kemi:
ose
Sepse , atëherë ka dy ndryshore të varura dhe një variabël të lirë.
Le të jetë x 1 një e panjohur e lirë, atëherë Ne e zgjidhim këtë sistem në çdo mënyrë dhe gjejmë zgjidhjen e përgjithshme të këtij sistemi: Sistemi themelor i zgjidhjeve përbëhet nga një zgjidhje, pasi n - r = 3 - 2 = 1.
Bashkësia e eigenvektorëve që i korrespondon vlerës vetjake λ = -1 ka formën: , ku x 1 është çdo numër tjetër nga zero. Le të zgjedhim një vektor nga ky grup, për shembull, duke vendosur x 1 = 1: .
Duke arsyetuar në mënyrë të ngjashme, gjejmë eigenvektorin që korrespondon me vlerën vetjake λ = 3: .
Në hapësirën R 3, baza përbëhet nga tre vektorë linearisht të pavarur, por kemi marrë vetëm dy eigenvektorë linearisht të pavarur, nga të cilët nuk mund të përbëhet baza në R 3. Rrjedhimisht, ne nuk mund ta reduktojmë matricën A të një operatori linear në formë diagonale.

Shembulli 13. Jepet një matricë .
1. Vërtetoni se vektori është eigenvektor i matricës A. Gjeni eigenvektorin që i korrespondon këtij vektori.
2. Gjeni një bazë në të cilën matrica A ka një formë diagonale.
Zgjidhje.
1. Nëse , atëherë është një vektor vetjak

.
Vektori (1, 8, -1) është një vektor vetjak. Eigenvalue λ = -1.
Matrica ka një formë diagonale në një bazë të përbërë nga eigenvektorë. Njëri prej tyre është i famshëm. Le të gjejmë pjesën tjetër.
Ne kërkojmë eigenvektorë nga sistemi:

Ekuacioni karakteristik: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Le të gjejmë eigenvektorin që korrespondon me vlerën vetjake λ = -3:

Rangu i matricës së këtij sistemi është dy dhe i barabartë me numrin e të panjohurave, kështu që ky sistem ka vetëm një zgjidhje zero x 1 = x 3 = 0. x 2 këtu mund të jetë çdo gjë tjetër përveç zeros, për shembull, x 2 = 1. Kështu, vektori (0 ,1,0) është një vektor vetjak që i përgjigjet λ = -3. Le të kontrollojmë:
.
Nëse λ = 1, atëherë marrim sistemin
Renditja e matricës është dy. Ne kryqëzojmë ekuacionin e fundit.
Le të jetë x 3 një e panjohur e lirë. Pastaj x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Duke supozuar x 3 = 1, ne kemi (-3,-9,1) - një vektor të veçantë që korrespondon me vlerën vetjake λ = 1. Kontrolloni:

.
Meqenëse vlerat vetjake janë reale dhe të dallueshme, vektorët që u korrespondojnë janë linearisht të pavarur, kështu që ato mund të merren si bazë në R3. Kështu, në bazë , , matrica A ka formën:
.
Jo çdo matricë e një operatori linear A:R n → R n mund të reduktohet në formë diagonale, pasi për disa operatorë linearë mund të ketë më pak se n eigjenvektorë të pavarur linearë. Sidoqoftë, nëse matrica është simetrike, atëherë rrënja e ekuacionit karakteristik të shumëfishimit m korrespondon saktësisht me m vektorë të pavarur linearisht.

Përkufizimi. Një matricë simetrike është një matricë katrore në të cilën elementet simetrike rreth diagonales kryesore janë të barabarta, domethënë në të cilën .
Shënime. 1. Të gjitha eigenvlerat e një matrice simetrike janë reale.
2. Eigenvektorët e një matrice simetrike që korrespondojnë me eigenvlera të ndryshme në çift janë ortogonale.
Si një nga aplikimet e shumta të aparatit të studiuar, ne konsiderojmë problemin e përcaktimit të llojit të një lakore të rendit të dytë.

www.site ju lejon të gjeni. Faqja kryen llogaritjen. Në pak sekonda serveri do të lëshohet zgjidhje e saktë. Ekuacioni karakteristik për matricën do të jetë një shprehje algjebrike e gjetur duke përdorur rregullin për llogaritjen e përcaktorit matricat matricat, ndërsa përgjatë diagonales kryesore do të ketë dallime në vlerat e elementeve diagonale dhe të ndryshores. Gjatë llogaritjes ekuacioni karakteristik për matricën në internet, çdo element matricat do të shumëzohet me elementët e tjerë përkatës matricat. Gjeni në modalitet online e mundur vetem per katror matricat. Gjetja e operacionit ekuacioni karakteristik për matricën në internet reduktohet në llogaritjen e shumës algjebrike të prodhimit të elementeve matricat si rezultat i gjetjes së përcaktorit matricat, vetëm për qëllim të përcaktimit ekuacioni karakteristik për matricën në internet. Ky operacion zë një vend të veçantë në teori matricat, ju lejon të gjeni eigenvlerat dhe vektorët duke përdorur rrënjët. Detyra e gjetjes ekuacioni karakteristik për matricën në internet përbëhet nga elementë shumëzues matricat e ndjekur nga përmbledhja e këtyre produkteve sipas një rregulli të caktuar. www.site gjen ekuacioni karakteristik për matricën dimensioni i dhënë në modalitet online. Llogaritja ekuacioni karakteristik për matricën në internet duke pasur parasysh dimensionin e tij, ky është gjetja e një polinomi me koeficientë numerikë ose simbolikë, i gjetur sipas rregullit për llogaritjen e përcaktorit. matricat- si shuma e prodhimeve të elementeve përkatëse matricat, vetëm për qëllim të përcaktimit ekuacioni karakteristik për matricën në internet. Gjetja e një polinomi në lidhje me një ndryshore për një kuadratik matricat, si përkufizim ekuacioni karakteristik për matricën, e zakonshme në teori matricat. Kuptimi i rrënjëve të një polinomi ekuacioni karakteristik për matricën në internet përdoret për të përcaktuar eigenvektorët dhe eigenvalues ​​për matricat. Për më tepër, nëse përcaktorja matricat do të jetë e barabartë me zero, atëherë ekuacioni karakteristik i matricës do të ekzistojë ende, ndryshe nga e kundërta matricat. Për të llogaritur ekuacioni karakteristik për matricën ose gjeni për disa në të njëjtën kohë ekuacionet karakteristike të matricave, ju duhet të shpenzoni shumë kohë dhe përpjekje, ndërsa serveri ynë do ta gjejë në pak sekonda ekuacioni karakteristik për matricën në internet. Në këtë rast, përgjigja për të gjetur ekuacioni karakteristik për matricën në internet do të jetë i saktë dhe me saktësi të mjaftueshme, edhe nëse numrat gjatë gjetjes ekuacioni karakteristik për matricën në internet do të jetë irracionale. Në faqen e internetit www.site hyrjet e karaktereve lejohen në elemente matricat, kjo eshte ekuacioni karakteristik për matricën në internet mund të paraqitet në formë të përgjithshme simbolike gjatë llogaritjes ekuacioni karakteristik i matricës në internet. Është e dobishme të kontrolloni përgjigjen e marrë gjatë zgjidhjes së problemit të gjetjes ekuacioni karakteristik për matricën në internet duke përdorur faqen www.site. Kur kryeni operacionin e llogaritjes së një polinomi - ekuacioni karakteristik i matricës, duhet të jeni të kujdesshëm dhe jashtëzakonisht të fokusuar kur zgjidhni këtë problem. Nga ana tjetër, faqja jonë do t'ju ndihmojë të kontrolloni vendimin tuaj për këtë temë ekuacioni karakteristik i një matrice në internet. Nëse nuk keni kohë për kontrolle të gjata të problemeve të zgjidhura, atëherë www.site sigurisht që do të jetë një mjet i përshtatshëm për të kontrolluar gjatë gjetjes dhe llogaritjes ekuacioni karakteristik për matricën në internet.

Përkufizimi 9.3. Vektor X thirrur vetvektor matricat A, nëse ka një numër të tillë λ, që barazia vlen: A X= λ X, pra rezultati i aplikimit në X transformimi linear i specifikuar nga matrica A, është shumëzimi i këtij vektori me numrin λ . Vetë numri λ thirrur eigenvalue matricat A.

Zëvendësimi në formula (9.3) x` j = λx j, marrim një sistem ekuacionesh për përcaktimin e koordinatave të vektorit vetjak:

. (9.5)

Kjo lineare sistem homogjen do të ketë një zgjidhje jo të parëndësishme vetëm nëse përcaktori kryesor i saj është 0 (rregulli i Cramer-it). Duke shkruar këtë kusht në formën:

marrim një ekuacion për përcaktimin e vlerave vetjake λ , thirri ekuacioni karakteristik. Shkurtimisht mund të përfaqësohet si më poshtë:

| A - λE | = 0, (9.6)

meqenëse ana e majtë e saj përmban përcaktorin e matricës A-λE. relativ polinom λ | A - λE| thirrur polinom karakteristik matricat A.

Vetitë e polinomit karakteristik:

1) Polinomi karakteristik i një transformimi linear nuk varet nga zgjedhja e bazës. Dëshmi. (shih (9.4)), por prandaj, . Kështu, nuk varet nga zgjedhja e bazës. Kjo do të thotë se | A-λE| nuk ndryshon kur kalon në një bazë të re.

2) Nëse matrica A transformimi linear është simetrike(ato. dhe ij =a ji), atëherë të gjitha rrënjët e ekuacionit karakteristik (9.6) janë numra realë.

Vetitë e eigenvlerave dhe eigenvektorëve:

1) Nëse zgjidhni një bazë nga eigenvektorët x 1, x 2, x 3 , që korrespondon me vlerat vetjake λ 1, λ 2, λ 3 matricat A, atëherë në këtë bazë transformimi linear A ka një matricë të formës diagonale:

(9.7) Vërtetimi i kësaj vetie rrjedh nga përkufizimi i vektorëve vetjak.

2) Nëse vlerat vetjake të transformimit A janë të ndryshëm, atëherë eigenvektorët e tyre përkatës janë linearisht të pavarur.

3) Nëse polinomi karakteristik i matricës A ka tre rrënjë të ndryshme, pastaj në disa baza matrica A ka pamje diagonale.

Le të gjejmë eigenvlerat dhe eigenvektorët e matricës Le të krijojmë një ekuacion karakteristik: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Le të gjejmë koordinatat e eigenvektorëve që korrespondojnë me secilën vlerë të gjetur λ. Nga (9.5) del se nëse X (1) ={x 1, x 2, x 3) – eigenvektor përkatës λ 1 =-2, atëherë

- një sistem bashkëpunues, por i pasigurt. Zgjidhja e saj mund të shkruhet në formë X (1) ={a,0,-a), ku a është çdo numër. Në veçanti, nëse kërkojmë që | x (1) |=1, X (1) =

Zëvendësimi në sistem (9.5) λ 2 =3, marrim një sistem për përcaktimin e koordinatave të vektorit të dytë eigjen - x (2) ={y 1, y 2, y 3}:

, ku X (2) ={b,-b,b) ose, me kusht | x (2) |=1, x (2) =

Për λ 3 = 6 gjeni vetvektorin x (3) ={z 1, z 2, z 3}:

, x (3) ={c,2c,c) ose në versionin e normalizuar

x (3) = Mund të vërehet se X (1) X (2) = ab–ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = p.e.s- 2bc + p.e.s= 0. Kështu, eigenvektorët e kësaj matrice janë dyshe ortogonale.

Leksioni 10.

Format kuadratike dhe lidhja e tyre me matricat simetrike. Vetitë e eigenvektorëve dhe eigjenvlerave të një matrice simetrike. Reduktimi i një forme kuadratike në formë kanonike.

Përkufizimi 10.1.Forma kuadratike variabla reale x 1, x 2,…, x n quhet një polinom i shkallës së dytë në këto ndryshore që nuk përmban një term të lirë dhe terma të shkallës së parë.

Shembuj të formave kuadratike:

(n = 2),

(n = 3). (10.1)

Le të kujtojmë përkufizimin e një matrice simetrike të dhënë në leksionin e fundit:

Përkufizimi 10.2. Matrica katrore quhet simetrike, nëse , domethënë nëse elementet e matricës që janë simetrike në lidhje me diagonalen kryesore janë të barabartë.

Vetitë e vlerave vetjake dhe eigjenvektorëve të një matrice simetrike:

1) Të gjitha eigenvlerat e një matrice simetrike janë reale.

Dëshmi (për n = 2).

Lëreni matricën A ka formën: . Le të krijojmë një ekuacion karakteristik:

(10.2) Le të gjejmë diskriminuesin:

Prandaj, ekuacioni ka vetëm rrënjë reale.

2) Eigenvektorët e një matrice simetrike janë ortogonale.

Dëshmi (për n= 2).

Koordinatat e vetvektorëve dhe duhet të plotësojnë ekuacionet.

SISTEMI I EKUACIONET LINEARE HOMOGJENE

Një sistem ekuacionesh lineare homogjene është një sistem i formës

Është e qartë se në këtë rast , sepse të gjithë elementët e njërës prej kolonave në këto përcaktorë janë të barabartë me zero.

Meqenëse të panjohurat gjenden sipas formulave , atëherë në rastin kur Δ ≠ 0, sistemi ka një zgjidhje unike zero x = y = z= 0. Megjithatë, në shumë probleme pyetja interesante është nëse një sistem homogjen ka zgjidhje të tjera nga zero.

Teorema. Në mënyrë që një sistem ekuacionesh homogjene lineare të ketë një zgjidhje jo zero, është e nevojshme dhe e mjaftueshme që Δ ≠ 0.

Pra, nëse përcaktorja Δ ≠ 0, atëherë sistemi ka një zgjidhje unike. Nëse Δ ≠ 0, atëherë sistemi i ekuacioneve homogjene lineare ka një numër të pafund zgjidhjesh.

Shembuj.

Eigenvektorët dhe eigjenvlerat e një matrice

Le të jepet një matricë katrore , X– disa matricë-kolona, ​​lartësia e së cilës përkon me rendin e matricës A. .

Në shumë probleme duhet të marrim parasysh ekuacionin për X

ku λ është një numër i caktuar. Është e qartë se për çdo λ ky ekuacion ka një zgjidhje zero.

Numri λ për të cilin ky ekuacion ka zgjidhje jo zero quhet eigenvalue matricat A, A X për të tillë λ quhet vetvektor matricat A.

Le të gjejmë eigenvektorin e matricës A. Sepse E∙X = X, atëherë ekuacioni i matricës mund të rishkruhet si ose . Në formë të zgjeruar, ky ekuacion mund të rishkruhet si një sistem ekuacionesh lineare. Vërtet .

Dhe për këtë arsye

Pra, kemi marrë një sistem ekuacionesh lineare homogjene për përcaktimin e koordinatave x 1, x 2, x 3 vektoriale X. Që një sistem të ketë zgjidhje jo zero është e nevojshme dhe e mjaftueshme që përcaktorja e sistemit të jetë e barabartë me zero, d.m.th.

Ky është një ekuacion i shkallës së 3-të për λ. Quhet ekuacioni karakteristik matricat A dhe shërben për të përcaktuar eigenvlerat e λ.

Çdo eigenvalue λ korrespondon me një vektor eigen X, koordinatat e të cilave përcaktohen nga sistemi në vlerën përkatëse të λ.

Shembuj.

ALGEBRA VEKTORIKE. KONCEPTI I VEKTORIT

Gjatë studimit të degëve të ndryshme të fizikës, ka sasi që përcaktohen plotësisht duke specifikuar vlerat e tyre numerike, për shembull, gjatësinë, sipërfaqen, masën, temperaturën, etj. Madhësi të tilla quhen skalare. Mirëpo, përveç tyre, ka edhe sasi, për të përcaktuar të cilat, përveç vlerës numerike, duhet të dihet edhe drejtimi i tyre në hapësirë, për shembull, forca që vepron në trup, shpejtësia dhe nxitimi i trupi kur lëviz në hapësirë, tension fushë magnetike në një pikë të caktuar të hapësirës, ​​etj. Madhësi të tilla quhen madhësi vektoriale.

Le të paraqesim një përkufizim të rreptë.

Segment i drejtuar Le të quajmë një segment, në lidhje me skajet e të cilit dihet se cili prej tyre është i pari dhe cili është i dyti.

Vektor quhet segment i drejtuar që ka një gjatësi të caktuar, d.m.th. Ky është një segment me një gjatësi të caktuar, në të cilin një nga pikat që e kufizojnë merret si fillim dhe e dyta si fund. Nëse A- fillimi i vektorit, Bështë fundi i tij, atëherë vektori shënohet me simbol përveç kësaj, vektori shpesh shënohet me një shkronjë të vetme; Në figurë, vektori tregohet me një segment, dhe drejtimi i tij me një shigjetë.

Moduli ose gjatësia Një vektor quhet gjatësia e segmentit të drejtuar që e përcakton atë. Shënuar me || ose ||.

Si vektorë do të përfshijmë gjithashtu të ashtuquajturin vektor zero, fillimi dhe fundi i të cilit përputhen. Është caktuar. Vektori zero nuk ka një drejtim specifik dhe moduli i tij është zero ||=0.

Vektorët quhen kolineare, nëse ndodhen në të njëjtën drejtëz ose në drejtëza paralele. Për më tepër, nëse vektorët dhe janë në të njëjtin drejtim, ne do të shkruajmë , të kundërt.

Vektorët e vendosur në drejtëza paralele me të njëjtin rrafsh quhen koplanare.

Të dy vektorët quhen të barabartë, nëse janë kolinear, kanë të njëjtin drejtim dhe janë të barabartë në gjatësi. Në këtë rast ata shkruajnë.

Nga përkufizimi i barazisë së vektorëve rezulton se një vektor mund të transportohet paralel me vetveten, duke e vendosur origjinën e tij në çdo pikë të hapësirës.

Për shembull.

OPERACIONET LINEARE MBI VEKTORËT

1. Shumëzimi i një vektori me një numër.

   Prodhimi i një vektori dhe numri λ është një vektor i ri i tillë që:

   Prodhimi i një vektori dhe një numri λ shënohet me .

   

   Për shembull, ekziston një vektor i drejtuar në të njëjtin drejtim me vektorin dhe me gjatësi sa gjysma e vektorit.

   Operacioni i prezantuar ka si më poshtë Vetitë:

2. Shtimi i vektorit.

   Le të jenë dhe dy vektorë arbitrarë. Le të marrim një pikë arbitrare O dhe ndërtoni një vektor. Pas kësaj nga pika A le të lëmë mënjanë vektorin. Vektori që lidh fillimin e vektorit të parë me fundin e të dytit quhet shuma të këtyre vektorëve dhe shënohet .

   

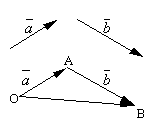
   Përkufizimi i formuluar i shtimit të vektorit quhet rregulli i paralelogramit, meqenëse e njëjta shumë vektorësh mund të merret si më poshtë. Le të shtyjmë nga pika O vektorët dhe . Le të ndërtojmë një paralelogram mbi këta vektorë OABC. Meqenëse vektorët, atëherë vektori, i cili është një diagonale e një paralelogrami të tërhequr nga kulmi O, padyshim do të jetë një shumë vektorësh.

   

   Është e lehtë të kontrollosh sa vijon vetitë e shtimit të vektorit.

3. Diferenca vektoriale.

   Një vektor kolinear me një vektor të caktuar, i barabartë në gjatësi dhe i drejtuar në të kundërt, quhet e kundërt vektor për një vektor dhe shënohet me . Vektori i kundërt mund të konsiderohet si rezultat i shumëzimit të vektorit me numrin λ = –1: .