Käänteimatriisin käänteismatriisirakenne. Korkeampi matematiikka

Tämä aihe on yksi vihatuimmista opiskelijoiden keskuudessa. Huonompia ovat todennäköisesti karsinnat.

Temppu on siinä, että käänteisen elementin käsite (enkä nyt puhu vain matriiseista) viittaa kertolaskuoperaatioon. Jopa sisään koulun opetussuunnitelma kertolaskuja monimutkainen toiminta, ja matriisikertominen on kokonaan erillinen aihe, jolle minulla on omistettu koko kappale ja video-opastus.

Tänään emme mene matriisilaskelmien yksityiskohtiin. Muistetaan vain: miten matriisit nimetään, miten ne kerrotaan ja mitä tästä seuraa.

Katsaus: Matriisimultiointi

Ensinnäkin sovitaan merkinnöistä. Matriisi $A$, jonka koko on $\left[ m\times n \right]$, on yksinkertaisesti numerotaulukko, jossa on täsmälleen $m$ riviä ja $n$ saraketta:

\=\aliviiva(\left[ \begin(matriisi) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matriisi) \oikea])_(n)\]

Jotta vältytään vahingossa sekoittamasta rivejä ja sarakkeita (usko minua, voit sekoittaa kokeessa yhden ja kaksi, puhumattakaan joistakin riveistä), katso vain kuvaa:

Indeksien määrittäminen matriisisoluille

Mitä tapahtuu? Jos asetat vakiokoordinaattijärjestelmän $OXY$ vasempaan yläkulmaan ja suuntaat akselit niin, että ne kattavat koko matriisin, tämän matriisin jokainen solu voidaan liittää yksilöllisesti koordinaatteihin $\left(x;y \right)$ - tämä on rivin numero ja sarakkeen numero.

Miksi koordinaattijärjestelmä on sijoitettu vasempaan yläkulmaan? Kyllä, koska juuri sieltä alamme lukea tekstejä. Se on erittäin helppo muistaa.

Miksi $x$-akseli on suunnattu alaspäin eikä oikealle? Jälleen, se on yksinkertaista: ota standardi koordinaattijärjestelmä ($x$-akseli menee oikealle, $y$-akseli nousee) ja kierrä sitä niin, että se peittää matriisin. Tämä on 90 asteen kierto myötäpäivään - näemme tuloksen kuvassa.

Yleisesti ottaen olemme selvittäneet kuinka määrittää matriisielementtien indeksit. Katsotaan nyt kertolaskua.

Määritelmä. Matriisit $A=\left[ m\times n \right]$ ja $B=\left[ n\times k \right]$, kun ensimmäisen sarakkeiden lukumäärä on sama kuin toisen rivien lukumäärä, ovat kutsutaan johdonmukaiseksi.

Juuri tuossa järjestyksessä. Voidaan hämmentyä ja sanoa, että matriisit $A$ ja $B$ muodostavat järjestetyn parin $\left(A;B \right)$: jos ne ovat johdonmukaisia ​​tässä järjestyksessä, ei ole ollenkaan välttämätöntä, että $B $ ja $ A $ ne. pari $\left(B;A \right)$ on myös johdonmukainen.

Vain yhteensopivia matriiseja voidaan kertoa.

Määritelmä. Sovittujen matriisien $A=\left[ m\times n \right]$ ja $B=\left[ n\times k \right]$ tulo on uusi matriisi $C=\left[ m\times k \right ]$ , jonka alkiot $((c)_(ij))$ lasketaan kaavan mukaan:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Toisin sanoen: saadaksesi matriisin $C=A\cdot B$ elementin $((c)_(ij))$, sinun on otettava ensimmäisen matriisin $i$-rivi, $j$ -toisen matriisin sarake, ja kerro sitten tämän rivin ja sarakkeen elementit pareittain. Laske tulokset yhteen.

Kyllä, se on niin kova määritelmä. Siitä seuraa välittömästi useita tosiasioita:

1. Matriisin kertolasku on yleisesti ottaen ei-kommutatiivista: $A\cdot B\ne B\cdot A$;
2. Kertominen on kuitenkin assosiatiivista: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
3. Ja jopa hajautetusti: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
4. Ja vielä kerran hajautetusti: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Kertolaskujakauma oli kuvattava erikseen vasemmalle ja oikealle summakertoimelle juuri kertolaskuoperaation ei-kommutatiivisuuden vuoksi.

Jos käy ilmi, että $A\cdot B=B\cdot A$, tällaisia ​​matriiseja kutsutaan kommutatiivisiksi.

Kaikkien matriisien joukossa, jotka kerrotaan jollakin siellä, on erityisiä - sellaisia, jotka kerrottuna millä tahansa matriisilla $A$ antavat jälleen $A$:

Määritelmä. Matriisia $E$ kutsutaan identiteetiksi, jos $A\cdot E=A$ tai $E\cdot A=A$. Tapauksessa neliömatriisi$A$ voimme kirjoittaa:

Identiteettimatriisi on usein vieras ratkaisemisessa matriisiyhtälöt. Ja ylipäätään, usein vieras matriisien maailmassa :)

Ja tämän $E$:n takia joku keksi kaiken hölynpölyn, joka kirjoitetaan seuraavaksi.

Mikä on käänteimatriisi

Koska matriisikertominen on erittäin työvoimavaltainen toimenpide (sinun täytyy kertoa joukko rivejä ja sarakkeita), konsepti käänteinen matriisi ei myöskään ole kaikkein triviaalisin. Ja vaatii selitystä.

Avaimen määritelmä

No, on aika tietää totuus.

Määritelmä. Matriisia $B$ kutsutaan matriisin $A$ käänteisarvoksi, jos

Käänteinen matriisi on merkitty $((A)^(-1))$ (ei pidä sekoittaa asteeseen!), joten määritelmä voidaan kirjoittaa uudelleen seuraavasti:

Vaikuttaa siltä, ​​​​että kaikki on erittäin yksinkertaista ja selkeää. Mutta kun tätä määritelmää analysoidaan, herää välittömästi useita kysymyksiä:

1. Onko käänteismatriisi aina olemassa? Ja jos ei aina, niin kuinka määrittää: milloin se on olemassa ja milloin ei?
2. Ja kuka sanoi, että on olemassa täsmälleen yksi tällainen matriisi? Entä jos jollekin alkumatriisille $A$ on kokonainen joukko käänteisiä?
3. Miltä kaikki nämä "käänteiset" näyttävät? Ja miten ne tarkalleen ottaen pitäisi laskea?

Mitä tulee laskenta-algoritmeihin, puhumme tästä hieman myöhemmin. Mutta vastaamme nyt jäljellä oleviin kysymyksiin. Muotoilkaamme ne erillisiksi lauseiksi-lemmiksi.

Perusominaisuudet

Aloitetaan siitä, miltä matriisin $A$ pitäisi periaatteessa näyttää, jotta $((A)^(-1))$ olisi olemassa sille. Nyt varmistamme, että näiden molempien matriisien on oltava neliön muotoisia ja samankokoisia: $\left[ n\times n \right]$.

Lemma 1. Annettu matriisi $A$ ja sen käänteinen $((A)^(-1))$. Sitten nämä molemmat matriisit ovat neliömäisiä ja samaa luokkaa $n$.

Todistus. Se on yksinkertaista. Olkoon matriisi $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Koska tulo $A\cdot ((A)^(-1))=E$ on määritelmän mukaan olemassa, matriisit $A$ ja $((A)^(-1))$ ovat johdonmukaisia ​​esitetyssä järjestyksessä:

\[\begin(tasaa) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( tasaa)\]

Tämä on suora seuraus matriisin kertolaskualgoritmista: kertoimet $n$ ja $a$ ovat "transit" ja niiden on oltava yhtä suuret.

Samalla määritellään myös käänteinen kertolasku: $((A)^(-1))\cdot A=E$, joten matriisit $((A)^(-1))$ ja $A$ ovat myös johdonmukainen määritetyssä järjestyksessä:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( tasaa)\]

Näin ollen yleisyyden menettämättä voidaan olettaa, että $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Kuitenkin määritelmän $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$ mukaan matriisien koot ovat täsmälleen samat:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Joten käy ilmi, että kaikki kolme matriisia - $A$, $((A)^(-1))$ ja $E$ - ovat neliömatriiseja, joiden koko on $\left[ n\times n \right]$. Lemma on todistettu.

No se on jo hyvä. Näemme, että vain neliömatriisit ovat käänteisiä. Varmistetaan nyt, että käänteinen matriisi on aina sama.

Lemma 2. Annettu matriisi $A$ ja sen käänteinen $((A)^(-1))$. Sitten tämä käänteismatriisi on ainoa.

Todistus. Mennään ristiriitaisesti: olkoon matriisilla $A$ vähintään kaksi käänteisarvoa - $B$ ja $C$. Sitten määritelmän mukaan seuraavat yhtäläisyydet ovat tosia:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(tasaa)\]

Lemmasta 1 päättelemme, että kaikki neljä matriisia - $A$, $B$, $C$ ja $E$ - ovat saman järjestyksen neliöitä: $\left[ n\times n \right]$. Siksi tuote määritellään:

Koska matriisin kertolasku on assosiatiivista (mutta ei kommutatiivista!), voimme kirjoittaa:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Nuori oikealle B=C. \\ \end(tasaa)\]

Saimme ainoan mahdollinen vaihtoehto: kaksi käänteismatriisin esiintymää ovat yhtä suuret. Lemma on todistettu.

Yllä olevat argumentit toistavat lähes sanatarkasti todisteen käänteiselementin ainutlaatuisuudesta kaikille reaalilukuille $b\ne 0$. Ainoa merkittävä lisäys on matriisien ulottuvuuden huomioon ottaminen.

Emme kuitenkaan vielä tiedä mitään siitä, onko jokainen neliömatriisi käännettävä. Tässä determinantti tulee avuksemme - tämä on keskeinen ominaisuus kaikille neliömatriiseille.

Lemma 3. Annettu matriisi $A$. Jos sen käänteimatriisi $((A)^(-1))$ on olemassa, niin alkuperäisen matriisin determinantti on nollasta poikkeava:

\[\left| A\oikea|\ne 0\]

Todistus. Tiedämme jo, että $A$ ja $((A)^(-1))$ ovat neliömatriiseja, joiden koko on $\left[ n\times n \right]$. Siksi jokaiselle niistä voimme laskea determinantin: $\left| A\right|$ ja $\left| ((A)^(-1)) \oikea|$. Tuotteen determinantti on kuitenkin yhtä suuri kuin determinanttien tulos:

\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \oikea|\]

Mutta määritelmän mukaan $A\cdot ((A)^(-1))=E$, ja $E$:n determinantti on aina yhtä suuri kuin 1, joten

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E\oikea|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \oikea|=1. \\ \end(tasaa)\]

Kahden luvun tulo on yhtä suuri kuin yksi vain, jos kukin näistä luvuista on nollasta poikkeava:

\[\left| A \right|\ne 0;\quad \left| ((A)^(-1)) \oikea|\ne 0.\]

Joten käy ilmi, että $\left| A \oikea|\ne 0$. Lemma on todistettu.

Itse asiassa tämä vaatimus on varsin looginen. Nyt analysoimme algoritmia käänteismatriisin löytämiseksi - ja tulee täysin selväksi, miksi nolladeterminantilla ei periaatteessa voi olla käänteismatriisia.

Mutta ensin muotoillaan "apu" määritelmä:

Määritelmä. Singulaarinen matriisi on neliömatriisi, jonka koko on $\left[ n\times n \right]$ ja jonka determinantti on nolla.

Siten voimme väittää, että jokainen käännettävä matriisi on ei-singulaarinen.

Kuinka löytää matriisin käänteisarvo

Nyt tarkastelemme universaalia algoritmia käänteisten matriisien löytämiseksi. Yleisesti ottaen on olemassa kaksi yleisesti hyväksyttyä algoritmia, ja tarkastelemme myös toista tänään.

Se, josta nyt keskustellaan, on erittäin tehokas matriiseille, joiden koko on $\left[ 2\times 2 \right]$ ja - osittain - koko $\left[ 3\times 3 \right]$. Mutta alkaen koosta $\left[ 4\times 4 \right]$, on parempi olla käyttämättä sitä. Miksi - nyt ymmärrät kaiken itse.

Algebralliset lisäykset

Valmistaudu. Nyt tulee kipua. Ei, älä huoli: kaunis sairaanhoitaja hameessa, pitsillä varustetut sukat eivät tule luoksesi ja anna ruiskeen pakaraan. Kaikki on paljon proosallisempaa: algebralliset lisäykset ja Hänen Majesteettinsa "Union Matrix" tulevat luoksesi.

Aloitetaan pääasiasta. Olkoon neliömatriisi, jonka koko on $A=\left[ n\times n \right]$, jonka alkioita kutsutaan nimellä $((a)_(ij))$. Sitten jokaiselle tällaiselle elementille voimme määrittää algebrallisen komplementin:

Määritelmä. Algebrallinen komplementti $((A)_(ij))$ elementille $((a)_(ij))$, joka sijaitsee matriisin $i$. rivillä ja $j$. sarakkeessa $A=\left[ n \times n \right]$ on muodon konstruktio

\[((A)_(ij))=((\vasen(-1 \oikea))^(i+j))\cdot M_(ij)^(*)\]

Missä $M_(ij)^(*)$ on matriisin determinantti, joka saadaan alkuperäisestä $A$:sta poistamalla sama $i$. rivi ja $j$. sarake.

Uudelleen. Matriisielementin algebrallinen komplementti, jonka koordinaatit on $\left(i;j \right)$, merkitään $((A)_(ij))$ ja lasketaan seuraavan kaavan mukaan:

1. Ensin poistetaan alkuperäisestä matriisista $i$-rivi ja $j$-:s sarake. Saadaan uusi neliömatriisi ja merkitään sen determinantti $M_(ij)^(*)$.
2. Sitten kerromme tämän determinantin arvolla $((\left(-1 \right))^(i+j))$ - tämä lause saattaa aluksi tuntua järkyttävältä, mutta pohjimmiltaan me vain selvitämme merkin edessä $M_(ij)^(*) $.
3. Laskemme ja saamme tietyn luvun. Ne. algebrallinen summaus on täsmälleen luku, ei jokin uusi matriisi jne.

Itse matriisia $M_(ij)^(*)$ kutsutaan lisämolliksi elementille $((a)_(ij))$. Ja tässä mielessä yllä oleva algebrallisen komplementin määritelmä on erikoistapaus monimutkaisemmasta määritelmästä - mitä tarkastelimme determinanttia koskevassa oppitunnissa.

Tärkeä huomautus. Itse asiassa "aikuisten" matematiikassa algebralliset lisäykset määritellään seuraavasti:

1. Otamme neliömatriisiin $k$ riviä ja $k$ saraketta. Niiden leikkauspisteessä saamme matriisin, jonka koko on $\left[ k\times k \right]$ - sen determinanttia kutsutaan kertaluvun $k$ minoriksi ja sitä merkitään $((M)_(k))$.
2. Sitten yliviivataan nämä "valitut" $k$ rivit ja $k$ sarakkeet. Jälleen kerran saat neliömatriisin - sen determinanttia kutsutaan lisämolliksi ja sitä merkitään $M_(k)^(*)$.
3. Kerro $M_(k)^(*)$ arvolla $((\left(-1 \right)))^(t))$, missä $t$ on (huomio nyt!) kaikkien valittujen rivien lukujen summa ja sarakkeet. Tämä on algebrallinen lisäys.

Katso kolmatta vaihetta: itse asiassa on 2 000 dollarin ehtojen summa! Toinen asia on, että arvolle $k=1$ saamme vain 2 termiä - nämä ovat samat $i+j$ - elementin $((a)_(ij))$ "koordinaatit", jolle olemme etsivät algebrallista komplementtia.

Joten tänään käytämme hieman yksinkertaistettua määritelmää. Mutta kuten myöhemmin näemme, se on enemmän kuin tarpeeksi. Seuraava asia on paljon tärkeämpi:

Määritelmä. Liittynyt matriisi $S$ neliömatriisiin $A=\left[ n\times n \right]$ on uusi matriisi, jonka koko on $\left[ n\times n \right]$, joka saadaan $A$ korvaamalla $(( a)_(ij))$ algebrallisilla lisäyksillä $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matriisi) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matriisi) \oikea]\]

Ensimmäinen ajatus, joka herää tämän määritelmän ymmärtämisen hetkellä, on "kuinka paljon pitää laskea!" Rentoudu: sinun täytyy laskea, mutta ei niin paljon :)

No, kaikki tämä on erittäin mukavaa, mutta miksi se on välttämätöntä? Mutta miksi.

Päälause

Palataanpa hieman taaksepäin. Muista, että Lemma 3 totesi, että käännettävä matriisi $A$ on aina ei-singulaarinen (eli sen determinantti on nollasta poikkeava: $\left| A \right|\ne 0$).

Joten, myös päinvastoin: jos matriisi $A$ ei ole singulaarinen, se on aina käännettävä. Ja $((A)^(-1))$:lle on jopa hakujärjestelmä. Tarkista se:

Käänteismatriisilause. Olkoon neliömatriisi $A=\left[ n\times n \right]$, ja sen determinantti on nollasta poikkeava: $\left| A \oikea|\ne 0$. Sitten käänteismatriisi $((A)^(-1))$ on olemassa ja se lasketaan kaavalla:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

Ja nyt - kaikki on sama, mutta luettavalla käsialalla. Käänteimatriisin löytämiseksi tarvitset:

1. Laske determinantti $\left| A \right|$ ja varmista, että se ei ole nolla.
2. Muodosta liittomatriisi $S$, ts. laske 100500 algebrallista lisäystä $((A)_(ij))$ ja aseta ne paikoilleen $((a)_(ij))$.
3. Transponoi tämä matriisi $S$ ja kerro se sitten jollain luvulla $q=(1)/(\left| A \right|)\;$.

Siinä kaikki! Käänteismatriisi $((A)^(-1))$ on löydetty. Katsotaanpa esimerkkejä:

\[\left[ \begin(matriisi) 3 & 1 \\ 5 & 2 \\\end(matriisi) \oikea]\]

Ratkaisu. Tarkastetaan käännettävyys. Lasketaan determinantti:

\[\left| A\oikea|=\vasen| \begin(matriisi) 3 & 1 \\ 5 & 2 \\\end(matriisi) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinantti on eri kuin nolla. Tämä tarkoittaa, että matriisi on käännettävä. Luodaan liittomatriisi:

Lasketaan algebralliset lisäykset:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \oikea|=2; \\ & ((A)_(12))=((\vasen(-1 \oikea))^(1+2))\cdot \left| 5 \oikea|=-5; \\ & ((A)_(21))=((\vasen(-1 \oikea))^(2+1))\cdot \left| 1 \oikea|=-1; \\ & ((A)_(22))=((\vasen(-1 \oikea))^(2+2))\cdot \left| 3\oikea|=3. \\ \end(tasaa)\]

Huomaa: determinantit |2|, |5|, |1| ja |3| ovat $\left[ 1\times 1 \right]$ kokoisten matriisien determinantteja eivätkä moduuleita. Ne. Jos determinanteissa oli negatiivisia lukuja, "miinusta" ei tarvitse poistaa.

Yhteensä liittomatriisimme näyttää tältä:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (taulukko)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]\]

No, siinä kaikki. Ongelma on ratkaistu.

Vastaus. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Tehtävä. Etsi käänteismatriisi:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right] \]

Ratkaisu. Laskemme determinantin uudelleen:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \right|=\begin(matriisi ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\vasen (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end(matriisi)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Determinantti on nollasta poikkeava - matriisi on käännettävä. Mutta nyt siitä tulee todella vaikeaa: meidän on laskettava jopa 9 (yhdeksän, perkele!) algebrallista lisäystä. Ja jokainen niistä sisältää determinantin $\left[ 2\times 2 \right]$. Lensi:

\[\begin(matriisi) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matriisi) 2 & -1 \\ 0 & 1 \\\end(matriisi) \right|=2; \\ ((A)_(12))=((\vasen(-1 \oikea))^(1+2))\cdot \left| \begin(matriisi) 0 & -1 \\ 1 & 1 \\\end(matriisi) \right|=-1; \\ ((A)_(13))=((\vasen(-1 \oikea))^(1+3))\cdot \left| \begin(matriisi) 0 & 2 \\ 1 & 0 \\\end(matriisi) \right|=-2; \\ ... \\ ((A)_(33))=((\vasen(-1 \oikea))^(3+3))\cdot \left| \begin(matriisi) 1 & -1 \\ 0 & 2 \\\end(matriisi) \right|=2; \\ \end(matriisi)\]

Lyhyesti sanottuna liittomatriisi näyttää tältä:

Siksi käänteinen matriisi on:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matriisi) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matriisi) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\end(array) \right]\]

Siinä se. Tässä on vastaus.

Vastaus. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \right ]$

Kuten näet, teimme jokaisen esimerkin lopussa tarkistuksen. Tältä osin tärkeä huomautus:

Älä ole laiska tarkistamaan. Kerro alkuperäinen matriisi löydetyllä käänteismatriisilla - sinun pitäisi saada $E$.

Tämän tarkistuksen suorittaminen on paljon helpompaa ja nopeampaa kuin virheen etsiminen lisälaskelmissa, kun esimerkiksi ratkaiset matriisiyhtälöä.

Vaihtoehtoinen tapa

Kuten sanoin, käänteismatriisilause toimii loistavasti kooissa $\left[ 2\times 2 \right]$ ja $\left[ 3\times 3 \right]$ (jälkimmäisessä tapauksessa se ei ole niin "hieno"" ), mutta matriiseille suuret koot suru alkaa.

Mutta älä huoli: on olemassa vaihtoehtoinen algoritmi, jolla voit rauhallisesti löytää käänteisen jopa matriisille $\left[10\times 10 \right]$. Mutta kuten usein tapahtuu, tämän algoritmin harkitsemiseksi tarvitsemme pienen teoreettisen johdannon.

Elementaariset muunnokset

Kaikkien mahdollisten matriisimuunnosten joukossa on useita erityisiä - niitä kutsutaan alkeismuunnoksiksi. Tällaisia ​​muunnoksia on tasan kolme:

1. Kertominen. Voit ottaa $i$:nnen rivin (sarakkeen) ja kertoa sen millä tahansa luvulla $k\ne 0$;
2. Lisäys. Lisää $i$. riville (sarakkeeseen) mikä tahansa muu $j$. rivi (sarake) kerrottuna millä tahansa luvulla $k\ne 0$ (voit tietysti tehdä $k=0$, mutta mikä on Mikään ei muutu?
3. Uudelleenjärjestely. Ota $i$. ja $j$. rivit (sarakkeet) ja vaihda paikkoja.

Miksi näitä muunnoksia kutsutaan alkeisarvoiksi (suurilla matriiseilla ne eivät näytä niin alkeisarvoisilta) ja miksi niitä on vain kolme - nämä kysymykset eivät kuulu tämän päivän oppitunnin piiriin. Siksi emme mene yksityiskohtiin.

Toinen asia on tärkeä: meidän on suoritettava kaikki nämä perversiot adjoint-matriisilla. Kyllä, kyllä: kuulit oikein. Nyt on vielä yksi määritelmä - viimeinen tämän päivän oppitunnilla.

Adjoint matriisi

Varmasti koulussa ratkaisit yhtälöjärjestelmiä summausmenetelmällä. No, vähennä toinen yhdestä rivistä, kerro jokin rivi luvulla - siinä kaikki.

Joten: nyt kaikki on ennallaan, mutta "aikuisen" tavalla. Oletko valmis?

Määritelmä. Olkoon matriisi $A=\left[ n\times n \right]$ annettu ja identiteettimatriisi$E$ on samankokoinen $n$. Sitten adjointtimatriisi $\left[ A\left| E\oikea. \right]$ on uusi matriisi, jonka koko on $\left[ n\times 2n \right]$ ja joka näyttää tältä:

\[\left[ A\left| E\oikea. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Lyhyesti sanottuna otamme matriisin $A$ ja oikealla osoitamme sille identiteettimatriisin $E$ oikean kokoinen, erottelemme ne pystyviivalla kauneuden vuoksi - tässä on liitteenä :)

Mikä vitsi on? Tässä on mitä:

Lause. Olkoon matriisi $A$ käännettävä. Tarkastellaan adjointmatriisia $\left[ A\left| E\oikea. \oikea]$. Jos käytät alkeellisia muunnoksia rivit tuo se muotoon $\left[ E\left| Kirkas. \right]$, ts. kertomalla, vähentämällä ja järjestämällä rivit uudelleen saadaksesi $A$:sta oikeanpuoleisen matriisin $E$, jolloin vasemmalla oleva matriisi $B$ on $A$:n käänteis:

\[\left[ A\left| E\oikea. \oikea]\vasemmalle[ E\left| Kirkas. \right]\Rightarrow B=((A)^(-1))\]

Se on niin yksinkertaista! Lyhyesti sanottuna algoritmi käänteismatriisin löytämiseksi näyttää tältä:

1. Kirjoita adjointmatriisi $\left[ A\left| E\oikea. \right]$;
2. Suorita perusmerkkijonon muunnoksia, kunnes $E$ tulee näkyviin $A$:n sijaan;
3. Tietysti jotain näkyy myös vasemmalla - tietty matriisi $B$. Tämä on päinvastoin;
4. VOITTO! :)

Tämä on tietysti paljon helpommin sanottu kuin tehty. Katsotaanpa siis pari esimerkkiä: koolle $\left[ 3\times 3 \right]$ ja $\left[ 4\times 4 \right]$.

Tehtävä. Etsi käänteismatriisi:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Ratkaisu. Luomme adjoint-matriisin:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Koska alkuperäisen matriisin viimeinen sarake on täytetty ykkösillä, vähennä ensimmäinen rivi lopuista:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\\end(matriisi)\to \\ & \to \vasemmalle [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Yksiköitä ei ole enempää, paitsi ensimmäinen rivi. Mutta emme koske siihen, muuten äskettäin poistetut yksiköt alkavat "kertyä" kolmannessa sarakkeessa.

Mutta voimme vähentää toisen rivin kahdesti viimeisestä - saamme yhden vasemmassa alakulmassa:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right]\begin(matriisi) \ \\ \downarrow \\ -2 \\\end(matriisi)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Nyt voimme vähentää viimeisen rivin ensimmäisestä ja kahdesti toisesta - näin "nollaamme" ensimmäisen sarakkeen:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matriisi) -1 \\ -2 \\ \uparrow \\\end(matriisi)\to \\ & \ \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(tasaa)\]

Kerro toinen rivi −1:llä ja vähennä se sitten 6 kertaa ensimmäisestä ja lisää 1 kerta viimeiseen:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matriisi) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end(matriisi)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matriisi) -6 \\ \ylänuoli \\ +1 \\\end (matriisi)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \right] \\ \end(tasaa)\]

Jäljelle jää vain rivien 1 ja 3 vaihtaminen:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(array) \right]\]

Valmis! Oikealla on vaadittu käänteimatriisi.

Vastaus. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \right ]$

Tehtävä. Etsi käänteismatriisi:

\[\left[ \begin(matriisi) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matriisi) \oikea]\]

Ratkaisu. Muodostamme adjungin uudelleen:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Itketään vähän, ollaan surullisia siitä, kuinka paljon meidän on nyt laskettava... ja alamme laskea. Ensin "nollataan" ensimmäinen sarake vähentämällä rivi 1 riveistä 2 ja 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(taulukko) \right]\begin(matriisi) \alasnuoli \\ -1 \\ -1 \\ \ \\\end(matriisi)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(tasaa)\]

Näemme liian monia "haittoja" riveillä 2-4. Kerro kaikki kolme riviä −1:llä ja polta sitten kolmas sarake vähentämällä rivi 3 lopuista:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matriisi) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end(matriisi)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (array) \right]\begin(matriisi) -2 \\ -1 \\ \ylänuoli \\ -2 \\\end(matriisi)\to \\ & \to \left[ \begin(array)( rrrr|. 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(tasaa)\]

Nyt on aika "paistaa" alkuperäisen matriisin viimeinen sarake: vähennä rivi 4 lopuista:

\[\begin(tasaa) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array ) \right]\begin(matriisi) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matriisi)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(tasaa)\]

Viimeinen heitto: "polttaa" toinen sarake vähentämällä rivi 2 riveistä 1 ja 3:

\[\begin(tasaa) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( taulukko) \right]\begin(matriisi) 6 \\ \nuoli ylös alas \\ -5 \\ \ \\\end(matriisi)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(tasaa)\]

Ja jälleen identiteettimatriisi on vasemmalla, mikä tarkoittaa, että käänteinen on oikealla :)

Vastaus. $\left[ \begin(matriisi) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matriisi) \oikea]$

Tarkastellaan matriisin kertolaskujen käänteisen toiminnan määrittelyn ongelmaa.

Olkoon A neliömatriisi, jonka kertaluku on n. Matriisi A^(-1), joka täyttää yhdessä annetun matriisin A kanssa yhtälöt:

A^(-1)\cdot A=A\cdot A^(-1)=E,

soitti päinvastoin. Matriisia A kutsutaan palautuva, jos sille on käänteinen, muuten - peruuttamaton.

Määritelmästä seuraa, että jos käänteismatriisi A^(-1) on olemassa, niin se on samaa suuruusluokkaa oleva neliö kuin A. Jokaisella neliömatriisilla ei kuitenkaan ole käänteisarvoa. Jos matriisin A determinantti on nolla (\det(A)=0), sillä ei ole käänteisarvoa. Itse asiassa soveltamalla lausetta identtisyysmatriisin E=A^(-1)A matriisien tulon determinantille saadaan ristiriita

\det(E)=\det(A^(-1)\cdot A)=\det(A^(-1))\det(A)=\det(A^(-1))\cdot0=0

koska identiteettimatriisin determinantti on yhtä suuri kuin 1. Osoittautuu, että neliömatriisin nollasta poikkeava determinantti on ainoa ehto käänteismatriisin olemassaololle. Muista, että neliömatriisia, jonka determinantti on yhtä suuri kuin nolla, kutsutaan yksiköksi (singulaariseksi), muuten sitä kutsutaan ei-degeneroituneeksi (ei-singulaariseksi).

Lause 4.1 käänteismatriisin olemassaolosta ja ainutlaatuisuudesta. Neliömatriisi A=\begin(pmatriisi)a_(11)&\cdots&a_(1n)\\ \vdots&\ddots&\vdots\\ a_(n1)&\cdots&a_(nn) \end(pmatriisi), jonka determinantti on nollasta poikkeava, on käänteinen matriisi ja lisäksi vain yksi:

A^(-1)=\frac(1)(\det(A))\cdot\! \begin(pmatrix)A_(11)&A_(21)&\cdots&A_(1n)\\ A_(12)&A_(22)&\cdots&A_(n2)\\ \vdots&\vdots&\ddots&\vdots\\ A_(1n) )&A_(2n)&\cdots&A_(nn) \end(pmatrix)= \frac(1)(\det(A))\cdot A^(+),

jossa A^(+) on matriisi, joka on transponoitu matriisille, joka koostuu matriisin A elementtien algebrallisista komplementeista.

Matriisia A^(+) kutsutaan adjoint matriisi matriisin A suhteen.

Itse asiassa matriisi \frac(1)(\det(A))\,A^(+) on olemassa ehdolla \det(A)\ne0 . On tarpeen osoittaa, että se on käänteinen A:lle, ts. täyttää kaksi ehtoa:

\begin(tasattu)\mathsf(1))&~A\cdot\!\left(\frac(1)(\det(A))\cdot A^(+)\right)=E;\\ \mathsf (2))&~ \!\left(\frac(1)(\det(A))\cdot A^(+)\right)\!\cdot A=E.\end(tasattu)

Todistetaan ensimmäinen yhtäläisyys. Huomautuksen 2.3 kohdan 4 mukaan determinantin ominaisuuksista seuraa, että AA^(+)=\det(A)\cdot E. Siksi

A\cdot\!\left(\frac(1)(\det(A))\cdot A^(+)\right)= \frac(1)(\det(A))\cdot AA^(+) = \frac(1)(\det(A))\cdot \det(A)\cdot E=E,

mikä piti näyttää. Toinen yhtäläisyys todistetaan samalla tavalla. Siksi ehdolla \det(A)\ne0 matriisilla A on käänteisarvo

A^(-1)=\frac(1)(\det(A))\cdot A^(+).

Osoitamme käänteismatriisin ainutlaatuisuuden ristiriitaisesti. Olkoon matriisin A^(-1) lisäksi toinen käänteimatriisi B\,(B\ne A^(-1)) siten, että AB=E. Kerrotaan tämän yhtälön molemmat puolet vasemmalta matriisilla A^(-1) , saadaan \aliviiva(A^(-1)AB)_(E)=A^(-1)E. Tästä syystä B=A^(-1) , mikä on ristiriidassa oletuksen B\ne A^(-1) kanssa. Siksi käänteinen matriisi on ainutlaatuinen.

Huomautukset 4.1

1. Määritelmästä seuraa, että matriisit A ​​ja A^(-1) ovat vaihdettavissa.

2. Ei-singulaarisen diagonaalimatriisin käänteisarvo on myös diagonaalinen:

\Bigl[\operaattorinnimi(diag)(a_(11),a_(22),\ldots,a_(nn))\Bigr]^(-1)= \operaattorinimi(diag)\!\left(\frac(1) )(a_(11)),\,\frac(1)(a_(22)),\,\ldots,\,\frac(1)(a_(nn))\oikea)\!.

3. Ei-singulaarisen alemman (ylemmän) kolmiomatriisin käänteisarvo on alempi (ylempi) kolmiomainen.

4. Elementaarisilla matriiseilla on käänteisiä, jotka ovat myös alkeismatriiseja (katso huomautusten 1.11 kappale 1).

Käänteimatriisin ominaisuudet

Matriisin inversiotoiminnolla on seuraavat ominaisuudet:

\begin(tasattu)\bold(1.)&~~ (A^(-1))^(-1)=A\,;\\ \lihavoitu(2.)&~~ (AB)^(-1 )=B^(-1)A^(-1)\,;\\ \lihavoitu(3.)&~~ (A^T)^(-1)=(A^(-1))^T\ ,;\\ \bold(4.)&~~ \det(A^(-1))=\frac(1)(\det(A))\,;\\ \bold(5.)&~~ E^(-1)=E\,. \end(tasattu)

jos yhtälöissä 1-4 määritellyt operaatiot ovat järkeviä.

Todistetaan ominaisuus 2: jos samaa kertaluokkaa olevien ei-singulaaristen neliömatriisien tulolla AB on käänteimatriisi, niin (AB)^(-1)=B^(-1)A^(-1).

Itse asiassa matriisien AB tulon determinantti ei ole nolla, koska

\det(A\cdot B)=\det(A)\cdot\det(B), Missä \det(A)\ne0,~\det(B)\ne0

Siksi käänteinen matriisi (AB)^(-1) on olemassa ja on ainutlaatuinen. Osoitetaan määritelmällä, että matriisi B^(-1)A^(-1) on matriisin AB käänteis. Todella.

Matriisia A -1 kutsutaan käänteismatriisiksi matriisin A suhteen, jos A*A -1 = E, missä E on n:nnen kertaluvun identiteettimatriisi. Käänteimatriisi voi olla olemassa vain neliömatriiseille.

Palvelun tarkoitus. Käyttämällä tästä palvelusta V online-tilassa löytyy algebrallisia komplementteja, transponoitua matriisia A T, liittoutumamatriisia ja käänteismatriisia. Päätös tehdään suoraan verkkosivustolla (online) ja se on ilmainen. Laskentatulokset esitetään raportissa Word- ja Excel-muodossa (eli on mahdollista tarkistaa ratkaisu). katso malliesimerkki.

Ohjeet. Ratkaisun saamiseksi on tarpeen määrittää matriisin ulottuvuus. Täytä seuraavaksi matriisi A uudessa valintaikkunassa.

Matriisiulottuvuus 2 3 4 5 6 7 8 9 10

Katso myös käänteinen matriisi Jordano-Gaussin menetelmällä

Algoritmi käänteismatriisin löytämiseksi

1. Transponoidun matriisin A T löytäminen.
2. Algebrallisten komplementtien määritelmä. Korvaa jokainen matriisin elementti sen algebrallisella komplementilla.
3. Käänteisen matriisin laatiminen algebrallisista lisäyksistä: tuloksena olevan matriisin jokainen elementti jaetaan alkuperäisen matriisin determinantilla. Tuloksena oleva matriisi on alkuperäisen matriisin käänteis.

Seuraavaksi algoritmi käänteismatriisin löytämiseksi samanlainen kuin edellinen lukuun ottamatta joitain vaiheita: ensin lasketaan algebralliset komplementit ja sitten määritetään liittoumatriisi C.

1. Määritä, onko matriisi neliö. Jos ei, niin sille ei ole käänteismatriisia.
2. Matriisin A determinantin laskeminen. Jos se ei ole nolla, jatkamme ratkaisua, muuten käänteismatriisia ei ole olemassa.
3. Algebrallisten komplementtien määritelmä.
4. Liittymämatriisin (keskinäinen, adjunktinen) täyttäminen C .
5. Käänteismatriisin laatiminen algebrallisista summauksista: adjointmatriisin C jokainen alkio jaetaan alkuperäisen matriisin determinantilla. Tuloksena oleva matriisi on alkuperäisen matriisin käänteis.
6. He tekevät tarkistuksen: he kertovat alkuperäisen ja tuloksena olevat matriisit. Tuloksena pitäisi olla identiteettimatriisi.

Esimerkki nro 1. Kirjoitetaan matriisi muotoon:

Algebralliset lisäykset.

A 1,1 = (-1) 1+1

-1 -2 5 4

∆ 1,1 = (-1 4-5 (-2)) = 6

A 1,2 = (-1) 1+2

2 -2 -2 4

∆ 1,2 = -(2 4-(-2 (-2))) = -4

A 1,3 = (-1) 1+3

2 -1 -2 5

∆ 1,3 = (2 5-(-2 (-1))) = 8

A 2,1 = (-1) 2+1

2 3 5 4

∆ 2,1 = -(2 4-5 3) = 7

A 2,2 = (-1) 2+2

-1 3 -2 4

∆ 2,2 = (-1 4-(-2 3)) = 2

A 2,3 = (-1) 2+3

-1 2 -2 5

∆ 2,3 = -(-1 5-(-2 2)) = 1

A 3,1 = (-1) 3+1

2 3 -1 -2

∆ 3,1 = (2 (-2)-(-1 3)) = -1

A 3,2 = (-1) 3+2

-1 3 2 -2

∆ 3,2 = -(-1 (-2)-2 3) = 4

A 3,3 = (-1) 3+3

-1 2 2 -1

∆ 3,3 = (-1 (-1)-2 2) = -3
Sitten käänteinen matriisi voidaan kirjoittaa näin:

A -1 = 1/10

6 -4 8 7 2 1 -1 4 -3

A -1 =

0,6 -0,4 0,8 0,7 0,2 0,1 -0,1 0,4 -0,3

Toinen algoritmi käänteismatriisin löytämiseksi

Esitetään toinen malli käänteismatriisin löytämiseksi.

1. Etsi annetun neliömatriisin A determinantti.
2. Löydämme algebrallisia komplementteja matriisin A kaikille elementeille.
3. Kirjoitamme rivielementtien algebrallisia lisäyksiä sarakkeisiin (transponointi).
4. Jaamme tuloksena olevan matriisin jokaisen elementin matriisin A determinantilla.

Kuten näemme, transponointioperaatiota voidaan soveltaa sekä alussa alkuperäiseen matriisiin että lopussa tuloksena oleviin algebrallisiin lisäyksiin.

Erikoistapaus: Identiteettimatriisin E käänteisarvo on identiteettimatriisi E.

Olkoon n:nnen kertaluvun neliömatriisi

Matriisia A -1 kutsutaan käänteinen matriisi suhteessa matriisiin A, jos A*A -1 = E, missä E on n:nnen kertaluvun identiteettimatriisi.

Identiteettimatriisi- sellainen neliömatriisi, jossa kaikki elementit ovat päädiagonaalia pitkin, joka kulkee vasemmalta yläkulma oikeassa alakulmassa on ykkösiä ja loput nollia, esimerkiksi:

Käänteinen matriisi voi olla olemassa vain neliömatriiseille ne. niille matriiseille, joissa rivien ja sarakkeiden määrä on sama.

Lause käänteismatriisin olemassaolon ehdolle

Jotta matriisilla olisi käänteimatriisi, on välttämätöntä ja riittävää, että se on ei-singulaarinen.

Matriisia A = (A1, A2,...A n) kutsutaan ei-degeneroitunut, jos sarakevektorit ovat lineaarisesti riippumattomia. Matriisin lineaarisesti riippumattomien sarakevektorien lukumäärää kutsutaan matriisin arvoksi. Siksi voidaan sanoa, että käänteisen matriisin olemassaoloon on välttämätöntä ja riittävää, että matriisin järjestys on yhtä suuri kuin sen ulottuvuus, ts. r = n.

Algoritmi käänteismatriisin löytämiseksi

1. Kirjoita matriisi A taulukkoon yhtälöjärjestelmien ratkaisemiseksi Gaussin menetelmällä ja anna sille matriisi E oikealle (yhtälöiden oikeanpuoleisen puolen tilalle).
2. Käytä Jordan-muunnoksia, vähennä matriisi A matriisiksi, joka koostuu yksikkösarakkeista; tässä tapauksessa on välttämätöntä muuttaa samanaikaisesti matriisi E.
3. Järjestä tarvittaessa viimeisen taulukon rivit (yhtälöt) uudelleen siten, että alkuperäisen taulukon matriisin A alle tulee identiteettimatriisi E.
4. Kirjoita muistiin käänteismatriisi A -1, joka sijaitsee viimeisessä taulukossa alkuperäisen taulukon matriisin E alla.

Esimerkki 1

Etsi matriisille A käänteismatriisi A -1

Ratkaisu: Kirjoitetaan matriisi A ja osoitetaan identiteettimatriisi E oikealle Jordan-muunnoksilla pelkistetään matriisi A identiteettimatriiksi E. Laskelmat on esitetty taulukossa 31.1.

Tarkistetaan laskelmien oikeellisuus kertomalla alkuperäinen matriisi A ja käänteimatriisi A -1.

Matriisin kertomisen tuloksena saatiin identiteettimatriisi. Siksi laskelmat on tehty oikein.

Vastaus:

Matriisiyhtälöiden ratkaiseminen

Matriisiyhtälöt voivat näyttää tältä:

AX = B, HA = B, AXB = C,

missä A, B, C ovat määritellyt matriisit, X on haluttu matriisi.

Matriisiyhtälöt ratkaistaan ​​kertomalla yhtälö käänteismatriiseilla.

Jos haluat esimerkiksi löytää matriisin yhtälöstä, sinun on kerrottava tämä yhtälö vasemmalla.

Siksi löytääksesi ratkaisun yhtälöön, sinun on löydettävä käänteinen matriisi ja kerrottava se yhtälön oikealla puolella olevalla matriisilla.

Muut yhtälöt ratkaistaan ​​samalla tavalla.

Esimerkki 2

Ratkaise yhtälö AX = B jos

Ratkaisu: Koska käänteimatriisi on yhtä suuri kuin (katso esimerkki 1)

Matriisimenetelmä taloudellisessa analyysissä

Muiden ohella niitä käytetään myös matriisimenetelmiä . Nämä menetelmät perustuvat lineaariseen ja vektori-matriisialgebraan. Tällaisia ​​menetelmiä käytetään monimutkaisten ja moniulotteisten taloudellisten ilmiöiden analysointiin. Useimmiten näitä menetelmiä käytetään, kun on tarpeen tehdä vertaileva arvio organisaatioiden ja niiden rakenteellisten jakojen toimivuudesta.

Matriisianalyysimenetelmien soveltamisprosessissa voidaan erottaa useita vaiheita.

Ensimmäisessä vaiheessa järjestelmä on muodostumassa taloudelliset indikaattorit ja sen perusteella kootaan lähdetietomatriisi, joka on taulukko, jonka yksittäisillä riveillä näytetään järjestelmänumerot (i = 1,2,....,n), ja pystysarakkeissa - indikaattorien numerot (j = 1,2,....,m).

Toisessa vaiheessa Jokaiselle pystysuoralle sarakkeelle tunnistetaan suurin käytettävissä olevista indikaattoriarvoista, joka otetaan yhdeksi.

Tämän jälkeen kaikki tässä sarakkeessa näkyvät summat jaetaan korkein arvo ja muodostetaan standardisoitujen kertoimien matriisi.

Kolmannessa vaiheessa kaikki matriisin komponentit on neliöity. Jos niillä on erilainen merkitys, jokaiselle matriisi-indikaattorille on määritetty tietty painokerroin k. Jälkimmäisen arvo määräytyy asiantuntijalausunnon perusteella.

Viimeisessä, neljäs vaihe löytyi luokitusarvoja Rj ryhmitellään niiden lisääntymisen tai laskun mukaan.

Esiteltyjä matriisimenetelmiä tulisi käyttää esimerkiksi silloin, kun vertaileva analyysi eri investointihankkeita, sekä arvioitaessa muita organisaatioiden taloudellisia indikaattoreita.

Käänteismatriisin löytäminen- ongelma, joka usein ratkaistaan ​​kahdella tavalla:

• algebrallinen summausmenetelmä, joka vaatii determinanttien etsimistä ja matriisien transponointia;
• eliminoimalla tuntematon Gauss, jossa on tarpeen suorittaa matriisien perusmuunnoksia (lisää rivejä, kerro rivit samalla numerolla jne.).

Niille, jotka ovat erityisen uteliaita, on olemassa muita menetelmiä, esimerkiksi lineaaristen muunnosten menetelmä. Tällä oppitunnilla analysoimme kolmea mainittua menetelmää ja algoritmia käänteismatriisin löytämiseksi näitä menetelmiä käyttämällä.

Käänteinen matriisi A, tällaista matriisia kutsutaan

A
. (1)

Käänteinen matriisi , joka on löydettävä tietylle neliömatriisille A, tällaista matriisia kutsutaan

jonka tulo matriisit A oikealla on identiteettimatriisi, ts.
. (1)

Identiteettimatriisi on diagonaalimatriisi, jossa kaikki diagonaaliset elementit ovat yhtä suuria kuin yksi.

Lause.Jokaiselle ei-singulaariselle (ei-degeneroituneelle, ei-singulaariselle) neliömatriisille löytyy käänteismatriisi, ja vain yksi. Erityiselle (degeneroituneelle, singulaariselle) neliömatriisille käänteismatriisia ei ole olemassa.

Neliömatriisia kutsutaan ei erikoista(tai ei-degeneroitunut, ei-yksikkö), jos sen determinantti ei ole nolla, ja erityistä(tai rappeutunut, yksikkö), jos sen determinantti on nolla.

Matriisin käänteisarvo löytyy vain neliömatriisista. Luonnollisesti käänteismatriisi on myös neliömäinen ja samaa luokkaa kuin annettu matriisi. Matriisia, jolle käänteismatriisi löytyy, kutsutaan käänteiseksi matriisiksi.

varten käänteinen matriisi On olemassa relevantti analogia luvun käänteisarvon kanssa. Jokaiselle numerolle a, ei ole nolla, on olemassa sellainen luku b että työ a Ja b vastaa yhtä: ab= 1. Määrä b kutsutaan luvun käänteiseksi b. Esimerkiksi luvun 7 käänteisluku on 1/7, koska 7*1/7=1.

Käänteismatriisin löytäminen algebrallisten lisäysten menetelmällä (liittoumatriisi)

Ei-singulaariselle neliömatriisille A käänteinen on matriisi

missä on matriisin determinantti A, a on matriisi, joka liittyy matriisiin A.

Liittynyt neliömatriisiin A on samaa kertaluokkaa oleva matriisi, jonka alkiot ovat matriisin determinantin vastaavien elementtien algebrallisia komplementteja transponoituna matriisin A suhteen.

Että

Ja

Algoritmi käänteismatriisin löytämiseksi algebrallisten summausten menetelmällä

1. Etsi tämän matriisin determinantti A. Jos determinantti on nolla, käänteimatriisin löytäminen pysähtyy, koska matriisi on singulaarinen ja sen käänteistä ei ole olemassa.

2. Etsi matriisi, joka on transponoitu suhteessa A.

3. Laske liittomatriisin alkiot vaiheessa 2 löydetyn maritzin algebrallisina komplementteina.

4. Käytä kaavaa (2): kerro matriisideterminantin käänteisarvo A, vaiheessa 4 löytyvään liittomatriisiin.

5. Tarkista vaiheessa 4 saatu tulos kertomalla tämä matriisi A käänteismatriisiin. Jos näiden matriisien tulo on yhtä suuri kuin identiteettimatriisi, niin käänteimatriisi löydettiin oikein. Muussa tapauksessa aloita ratkaisuprosessi uudelleen.

Esimerkki 1. Matriisille

etsi käänteinen matriisi.

Ratkaisu. Käänteisen matriisin löytämiseksi sinun on löydettävä matriisin determinantti A. Löydämme kolmioiden säännön mukaan:

Siksi matriisi A– ei-singulaarinen (ei-degeneroitunut, ei-singulaarinen) ja sille on käänteinen.

Etsitään tähän matriisiin liittyvä matriisi A.

Etsitään matriisi transponoituna suhteessa matriisiin A:

Laskemme liittoutumatriisin elementit matriisin suhteen transponoidun matriisin algebrallisina komplementteina A:

Siksi matriisi liittoutui matriisiin A, sillä on muoto

Kommentti. Järjestys, jossa elementit lasketaan ja matriisi transponoidaan, voi olla erilainen. Voit ensin laskea matriisin algebralliset komplementit A, ja transponoi sitten algebrallinen komplementtimatriisi. Tuloksena tulisi olla samat liittomatriisin elementit.

Kaavaa (2) soveltamalla löydämme matriisin käänteisen matriisille A:

Käänteismatriisin löytäminen Gaussin tuntemattoman eliminointimenetelmän avulla

Ensimmäinen askel matriisin käänteisarvon löytämiseksi Gaussin eliminointimenetelmää käyttämällä on kohdistaminen matriisiin A Saman järjestyksen identiteettimatriisi erottaen ne pystypalkilla. Saamme kaksoimatriisin. Kerrotaan tämän matriisin molemmat puolet luvulla , niin saadaan

,

Algoritmi käänteismatriisin löytämiseksi Gaussin tuntemattoman eliminointimenetelmän avulla

1. Matriisiin A määrittää samaa järjestystä oleva identiteettimatriisi.

2. Muunna tuloksena oleva kaksoimatriisi siten, että sen vasemmalle puolelle saadaan yksikkömatriisi, sitten oikealle puolelle identiteettimatriisin tilalle automaattisesti käänteimatriisi. Matrix A vasemmalla puolella muunnetaan identiteettimatriisiksi alkeismatriisimuunnoksilla.

2. Jos matriisimuunnosprosessissa A identiteettimatriisissa on vain nollia millä tahansa rivillä tai missä tahansa sarakkeessa, jolloin matriisin determinantti on yhtä suuri kuin nolla, ja näin ollen matriisi A on yksikkö, eikä sillä ole käänteismatriisia. Tässä tapauksessa käänteismatriisin lisämäärittely pysähtyy.

Esimerkki 2. Matriisille

etsi käänteinen matriisi.

ja muunnamme sen niin, että vasemmalla puolella saamme identiteettimatriisin. Aloitamme muutoksen.

Kerro vasemman ja oikean matriisin ensimmäinen rivi (-3) ja lisää se toiseen riviin ja kerro sitten ensimmäinen rivi (-4) ja lisää se kolmanteen riviin, niin saadaan

.

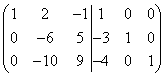Eli jos mahdollista ei ole murtolukuja seuraavien muunnosten aikana luomme ensin yksikön toiselle riville kaksoimatriisin vasemmalle puolelle. Voit tehdä tämän kertomalla toisen rivin 2:lla ja vähentämällä siitä kolmannen rivin, niin saamme

.

Lisätään ensimmäinen rivi toiseen ja kerrotaan sitten toinen rivi (-9) ja lisätään se kolmannella rivillä. Sitten saamme

.

Jaa sitten kolmas rivi 8:lla

.

Kerro kolmas rivi kahdella ja lisää se toiselle riville. Siitä käy ilmi:

.

Vaihdetaan toinen ja kolmas rivi, niin lopulta saadaan:

.

Näemme, että vasemmalla puolella meillä on identiteettimatriisi, joten oikealla puolella on käänteismatriisi. Siten:

.

Voit tarkistaa laskelmien oikeellisuuden kertomalla alkuperäisen matriisin löydetyllä käänteismatriisilla:

Tuloksena pitäisi olla käänteinen matriisi.

Esimerkki 3. Matriisille

etsi käänteinen matriisi.

Ratkaisu. Kaksoismatriisin laatiminen

ja muutamme sen.

Kerromme ensimmäisen rivin 3:lla ja toisen 2:lla ja vähennämme toisesta, ja sitten kerromme ensimmäisen rivin viidellä ja kolmannen 2:lla ja vähennämme kolmannesta rivistä, niin saamme

.

Kerromme ensimmäisen rivin kahdella ja lisäämme sen toiseen ja vähennämme sitten toisen kolmannesta rivistä, niin saamme

.

Näemme, että vasemman puolen kolmannella rivillä kaikki elementit ovat yhtä suuria kuin nolla. Siksi matriisi on singulaarinen eikä siinä ole käänteismatriisia. Lopetamme käänteisen maritzin etsimisen.